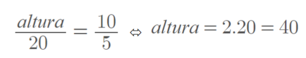Teorema de Tales (interseção)

O teorema de Tales é um teorema da geometria que afirma que, num plano, a interseção de retas paralelas, por retas transversais, formam segmentos proporcionais.[2] Em inglês, é conhecido como o Intercept theorem (Teorema da Interseção);[3] em alemão, chama-se Strahlensatz,[4] isto é, o teorema dos raios.

Este teorema é atribuído ao matemático e filósofo grego Tales de Mileto. Esta atribuição é explicada a partir de uma lenda, na qual Tales calcularia a altura de uma pirâmide (pirâmide de Quéops) medindo o comprimento da sua sombra no solo e o comprimento da sombra de um bastão (anteparo) de determinada altura.[5] No entanto, a mais antiga prova escrita conhecida deste teorema é dada em Elementos de Euclides (Proposição 2 do Livro VI).[6] É baseado na proporcionalidade de áreas de triângulos.
O teorema de Tales é generalizado em maior dimensão. As observações são equivalentes às observações da geometria projetiva,que é a preservação da relações transversais por projeções.[7][8] Em um nível mais básico, o teorema de Tales é usado para calcular comprimentos trigonométricos, desde que duas linhas paralelas estejam disponíveis.[9] Esta propriedade é usada em instrumentos de cálculo de comprimento.
Em inglês e alemão, o teorema de Tales designa outro teorema da geometria que afirma que um triângulo inscrito em um círculo, e do qual um lado é um diâmetro, é um triângulo retângulo.
Babilónia[editar | editar código-fonte]


A Tábua MLC 1950 (c. 1900–1600 a.C.)[10] contém uma breve descrição do exercício em que um escriba tenta calcular a base de um retângulo trapezóide a partir da informação da área do trapézio (S), a altura do trapézio e a altura do triângulo completam a altura da figura ABC. No problema foram fornecidos os dois comprimentos AD e DB, bem como a área do trapézio BCED (ver figura em anexo)[11][12]. O escriba calcula:
- a meia-soma dos comprimentos BC e DE pela razão da área pela altura (de outras tábuas confirma-se que a fórmula que dava a área do trapézio já era conhecida).
- a meia-diferença, pela aplicação de uma fórmula:
Demonstração:
Se chamamos "F" o ponto tal que "BDEF" é um retângulo, a proporcionalidade dos triângulos "ABC", "ADE" e "EFC" dá:
Ou ainda :
portanto:
E pela soma :
por consequência :
Logo,
Antigo Egito[editar | editar código-fonte]

Da civilização egípcia, apenas quatro papiros oferecem resoluções de problemas matemáticos. Os egiptólogos deduzem indiretamente o conhecimento matemático do Antigo Egipto a partir de documentos administrativos que lidam com as inundações do Nilo, o cálculo de impostos, a distribuição de terras aráveis, a distribuição de campos após a destruição de marcos (sinalizadores de fronteira) após inundações. De acordo com alguns egiptólogos, as pirâmides de Guizé mostram um conhecimento geométrico posto a serviço da arquitetura. No entanto, de acordo com outros egiptólogos, a ausência de tabelas numéricas mostra um baixo interesse pela matemática (fora de suas aplicações).[13]
O mais famoso dos quatro papiros é o papiro Rhind, em homenagem a Alexander Henry Rhind (1833-1863), antiquário escocês que comprou o papiro em 1858. Foi escrito pelo escriba Ahmès sob o faraó Apopi I (por volta de 1550 a.C.), reescrevendo o conteúdo de um papiro (não encontrado) escrito durante o reinado do faraó Amenemés II (cerca 1850 a.C.).
A egiptóloga Sylvia Couchoud está a estudar esse papiro com atenção. Além das informações que ele fornece sobre conhecimento de aritmética e de álgebra, ele oferece a afirmação do teorema de Tales,[14] chamado seqet, aplicado a um exemplo numérico.[carece de fontes]
Grécia Antiga[editar | editar código-fonte]

A antiga civilização grega é diferente da do Egito e da Babilónia. Filosofia e beleza são tópicos essenciais. Não surpreende, portanto, que a matemática grega não tenha como objetivo essencial a resolução de problemas pragmáticos do quotidiano, mas de problemas teóricos. Pitágoras estabelece uma geometria baseada em princípios, que posteriormente se tornarão axiomas para acessar uma abordagem não experimental e puramente especulativa e intelectual. Para Platão, a matemática é a base do ensino dos reis-filósofos da cidade-estado ideal. A geometria realmente tem raízes na civilização grega.[15]
Uma visão dessa natureza altera radicalmente a formulação do teorema de Tales, que encontramos a primeira demonstração escrita conhecida nos Elementos de Euclides. Três elementos essenciais mudaram. O teorema é declarado de maneira muito geral/generalizado, ao contrário dos egípcios que descrevem o teorema com a ajuda de um exemplo, ou babilónios que usam o teorema implicitamente. Anteriormente, a matemática consiste de um conjunto de métodos capazes de chegar ao resultado esperado pela experiência.A demonstração estava ausente. Finalmente, o teorema recíproco é criado e usado. Sendo que, o teorema recíproco é o contrário de um teorema; por exemplo:[16][17]
Se A então B (teorema) ->Se B então A (teorema recíproco)
É de notar que nem sempre é possivel formular um teorema recíproco
Simplificação do teorema[editar | editar código-fonte]
Para simplificar o teorema precisamos de uma formulação simplificada:
Teorema — "Se cortarmos duas retas quaisquer por várias retas paralelas, os segmentos correspondentes determinados em ambas são proporcionais"

Demonstrações[editar | editar código-fonte]
Visão 3D[editar | editar código-fonte]
Na geometria espacial o teorema surge no tratamento das secções de um sólido por um plano paralelo à base. Na perspectiva, ele surge quando se estudam as propriedades das figuras geométricas que se conservam quando traçadas em um plano e projetadas em outro plano a partir de uma fonte no infinito; dessas propriedades (conservação do ponto médio, conservação do baricentro, conservação do alinhamento, etc..), a fundamental, é a conservação das razões das distâncias entre pontos alinhados. Na figura abaixo temos duas representações de um quadrado em dois planos distintos. Os pontos A,B e C alinhados do primeiro quadrado e os pontos correspondentes D, E e F no outro plano têm como invariante fundamental a conservação das razões: AC/AB=DF/DE.[19]

Assim podemos reparar que houve uma deformação, ou seja, o plano com os pontos D, E, F não é paralelo com o plano com os pontos A, B, C.
Vetores-Multiplicação de vetores por escalares (números popularmente ditos)[editar | editar código-fonte]
No estudo da geometria vetorial, o teorema de Tales assegura a propriedade: λ(a+b)=λ.a +λ.b com λ ∈ IR. As duas configurações abaixo correspondem aos casos em que α > 0 e α < 0. O teorema de Tales faz-se necessário para justificar esta propriedade se não quisermos considerá-la como axioma.

Daí segue-se que  , ou seja existe proporcionalidade entre os comprimentos dos vetores (normas de vetores).[20]
, ou seja existe proporcionalidade entre os comprimentos dos vetores (normas de vetores).[20]
Áreas[editar | editar código-fonte]
Sejam ABC um triângulo e D um ponto entre A e B. Tracemos pelo ponto D uma reta r paralela ao lado BC com r ∩ AC= E. Provemos que AD/DB=AE/EC.

A área do triângulo ADE pode ser calculada de duas maneiras AD.EF/2 ou AE.DG/2 Da igualdade das duas expressões conclui-se que AD.EF=AE.DG (1)
Os triângulos BDE e CED têm áreas iguais (mesma base DE e mesma altura ).
Logo DB.EF/2=EC.DG/2.(2)
De (1) e (2) vem: AD/AE=DB/EC ou AD/DB=AE/EC[21]

Semelhança de triângulos[editar | editar código-fonte]
A semelhança de triângulos é uma aplicação do teorema de Tales aos triângulos. Relembremos que:
"Se cortarmos duas retas quaisquer por várias retas paralelas, os segmentos correspondentes determinados em ambas são proporcionais".
A função das "duas retas quaisquer" desempenha o segmento de reta DA e o segmento de reta AE. E, por consequência, os "segmentos determinados" são AB, BD, AC, CE, BC e DE.
Assim estabelecemos que:


Também podemos deduzir as relações entre os perímetros dos triângulos, tal como, deduzir as relações entre as áreas de triângulos:
, em que 'A' é a área do triângulo maior e 'a' é a área do triângulo menor
, em que 'P' é o perímetro do triângulo maior e 'p' é o perímetro da área menor[22]
Demonstração algébrica simplificada[editar | editar código-fonte]
[23]A partir da figura que segue podemos demonstrar a veracidade do teorema. Se o teorema está correto, podemos concluir que a (número que alterou do comprimento formando a.m) terá de ser igual a e/d (que é a mesma coisa que d/e=1/a):

De uma forma mais simples: Nós aplicamos a mudança 'a' e é igual à razão 'e/d', ou seja 'e/d' é a razão de proporcionalidade em ambas as retas não paralelas. Dizendo por outras palavras, 'a' e 'e/d' são iguais, isto é, as 'mudanças' são iguais.[24]
Geometria projetiva (relação)[editar | editar código-fonte]
Na geometria projetiva, o teorema de Tales ou seu recíproco pode ser usado para estabelecer condições de paralelismo. O teorema de Tales pode ser usado como uma substituição das homotetias em demonstrações.[25]
Teorema — Dado um triângulo ABC e três pontos A, B e C respectivamente pertencentes às linhas retas (BC), (AC) e (AB); os pontos A, B e C estão alinhados se:
Teorema — Dado um triângulo ABC e três pontos D, E e F respectivamente pertencentes às linhas retas (BC), (AC) e (AB); as linhas (AF), (BD) e (CE) são simultâneas ou paralelas, se
Teorema — Posicionando-se dois triângulos ABC e A'B'C 'de tal forma que as linhas (AB) e (A'B') sejam paralelas, da mesma forma para (BC) e (B'C ') e para (AC) e (A'C '). Então as linhas (AA '), (BB') e (CC ') são paralelas ou concorrentes.
Teorema — Dadas duas linhas de d e; três pontos A, B e C de d; três pontos A', B' e C' de d'. Denotamos por P, Q e R as respectivas interseções de (AB ') e (A'B), (B'C) e (BC'), e (AC') e (A'C). Então os pontos D, E e F estão alinhados.
Utilizações[editar | editar código-fonte]
Calcular o comprimento de uma ponte[editar | editar código-fonte]

Seguindo o Teorema de Tales, pode-se estabelecer a seguinte relação:[26]
Assim pode-se chegar à relação:
Calcular a altura de edifícios[editar | editar código-fonte]


Através do Teorema de Tales, podemos estabelecer as relações:
Para perceber isto releia a secção da Semelhança de Triângulos
Ou seja, generalizando:
Teorema da ligação dos pontos médios de dois lados de um triângulo[editar | editar código-fonte]

Este teorema defende que a ligação de dois pontos médios (neste caso D e E) de dois lados do triângulo (AB e AC) forma um segmento correspondente à metade do triângulo inicial (neste caso ABC).[27]
Isto deve-se ao facto de que (seguindo o teorema de Tales) temos retas transversais (AB e AC) e retas paralelas (DE e BC), além disso, AB=AD+DB e AC=AE+EC, ou seja:
Assim deduz-se que:
Trigonometria[editar | editar código-fonte]

O Teorema de Tales, mais em específico a semelhança de triângulos, explica as razões trigonométricas e a conservação das mesmas pelos ângulos.
Na semelhança de triângulos existe um postulado que indica que os triângulos são semelhantes se os ângulos forem iguais.
Através do Teorema de Tales podemos estabelecer as seguintes razões:
De tal modo, também é possível retirar outras razões trigonométricas (ver no artigo principal)[28]
Desenho geométrico[editar | editar código-fonte]

No desenho geométrico o teorema aplica-se às construções que dividem um segmento em partes iguais ou proporcionais; a determinação da 3ª e 4ª proporcionais são aplicações diretas do mesmo.[2]
Construção com régua e compasso[editar | editar código-fonte]
Para a divisão do segmento AB em partes iguais ou proporcionais, faça o seguinte:
- Desenhe, a partir de A, dois segmento de reta, que formem um ângulo agudo, reto ou obtuso.
- A partir de A marque com o compasso duas medidas quaisquer, AE e EC, em um dos segmentos.
- Agora a partir de C trace uma reta qualquer que intercepte o outro segmento num ponto B.
- A partir de E trace uma reta paralela ao segmento BC.
- O ponto D encontrado divide os segmentos, que concorrem no ponto A, em partes proporcionais.
- Se AE e EC tiverem a mesma medida, então a divisão desenhada também terá partes iguais.
Todas as leituras do desenho geométrico[editar | editar código-fonte]
- AD está para AB, assim como AE está para AC. (leitura da legenda)
- DB está para AB, assim como EC está para AC. (leitura da legenda)
- AB está para AD, assim como AC está para AE.
- AB está para DB, assim como AC está para EC.
- AD está para DB, assim como AE está para EC.
- DB está para AD, assim como EC está para AE.
Ver também[editar | editar código-fonte]
- Lista de construções do desenho geométrico
- Teorema de Pitágoras
- Trigonometria
- Semelhança de Triângulos
- Teorema de Menelaus
- Teorema de Ceva
- Teorema Pappus
- Teorema de Desargues
Referências
- ↑ Mandarino, Denis - Desenho Geométrico, construções com régua e compasso. Ed. Plêiade, São Paulo, 2007, p. 31.
- ↑ a b Putnoki, José Carlos - Elementos de Geometria e desenho geométrico. Vol. 1. Ed. Scipione, São Paulo, 1989, p. 112 e 114
- ↑ Böhmermann. «Easy proof of the intercept theorem». Consultado em 18 de agosto de 2019
- ↑ (sem último nome), Enyalia (24 de abril de 2019). «Strahlensatz». Wikipédia alemã. Consultado em 18 de agosto de 2019
- ↑ «Tales de Mileto». Universidade de Lisboa. Consultado em 18 de agosto de 2019
- ↑ Luís, Rafael (Fevereiro 2005). «Elementos de Euclides» (PDF). Universidade da Madeira. Consultado em 18 de agosto de 2019
- ↑ Атанасян (Atanasyan), Левон Сергеевич (Levon Sergeevich). «Geometria» (PDF). Consultado em 18 de agosto de 2019
- ↑ Bénéat, Donatien (Janeiro 2008). «Geometria projetiva» (PDF). Consultado em 18 de agosto de 2019
- ↑ Moreira, Luiz Paulo. «O que é razão trigonométrica?». BRASIL ESCOLA. Consultado em 18 de agosto de 2019
- ↑ Renzetti, Roberto. «Algumas questões na Matemática Antiga» (PDF). Consultado em 20 de Agosto de 2019
- ↑ Caratini, Roger (2004). Os matemáticos da Babilónia. [S.l.: s.n.] 205 páginas
- ↑ Neugebauer, Otto (1945). Mathematical Cuneiform Texts. [S.l.]: American Oriental Society. 48 páginas
- ↑ Erman, Adolf. «A vida no Antigo Egipto». London Macmillan and Co.
- ↑ «Sylvia Couchoud». Consultado em 20 de Agosto de 2019
- ↑ «Platão». Só Matemática. Consultado em 19 de Agosto de 2019
- ↑ de Alexandria, Euclides. «Os Elementos» (PDF). Livros grátis. Consultado em 20 de Agosto de 2019
- ↑ Vitrac, Bernard (2004). A origem da matemática grega. [S.l.]: Génies de la Science
- ↑ Bongiovanni, Vincenzo (2007). «teorema de Tales» (PDF). Projeto APOEMA. Consultado em 20 de Agosto de 2019
- ↑ «Teorema de Tales». Ilemaths. Consultado em 20 de Agosto de 2019
- ↑ Martins, Ricardo (5 de Abril de 2013). «Geometria Analítica e Vetores - Aula 6 - Método prático para inverter vetores - parte 2». UNIVESP. Consultado em 20 de Agosto de 2019
- ↑ Araújo, Marcos (12 de Agosto de 2014). «Geometria - Aula 58 - Teorema de Tales através de áreas». Programa de Iniciação Cientifica da OBMEP. Consultado em 20 de Agosto de 2019
- ↑ «Semelhança de triângulos» (PDF). Grandes Ideias. Consultado em 20 de Agosto de 2019
- ↑ «Teorema de Thales de Mileto primeiro, segundo e exemplos». Thpanorama. Consultado em 20 de Agosto de 2019
- ↑ «Teorema da proporcionalidade básica e Teorema de Tales». Toppr. Consultado em 3 de outubro de 2019
- ↑ Carlos T. de C. Auffinger, Antonio (Setembro de 2003). «Introdução à Geometria Analítica» (PDF). Universidade Federal do Espírito Santo. Consultado em 20 de Agosto de 2019
- ↑ Neves, Maria. Matemática - 7.º Ano. [S.l.]: Porto editora. 90 páginas
- ↑ Forti, Enrico (1885). Geometria analítica. [S.l.: s.n.] 34 páginas
- ↑ Bongiovanni, Vincenzo. «O Teorema de Tales: uma ligação entre o geométrico e o numérico». Revista Eletrônica de Educação Matemática. Consultado em 20 de Agosto de 2019







![{\displaystyle A[ADE]={FE.AD \over 2}={DG.AE \over 2}<=>{FE.AD}={DG.AE}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82854f63263089a945b39696e94bb765f0ced8e8)
![{\displaystyle A[BDE]=A[CED]={DB.EF \over 2}={EC.DG \over 2}<=>{DB.EF}={EC.DG}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9077a563900523ef389ad20518c02bc70efcbcd3)