Usuário(a):MGromov/TestesPasseioAleatório2
Este artigo não cita fontes confiáveis. (Abril de 2012) |


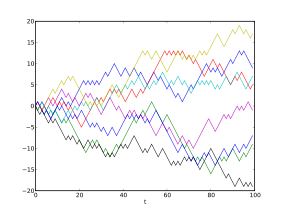
Um passeio aleatório é um objeto matemático que descreve um caminho que consiste de uma sucessão de passos aleatórios. Por exemplo, o caminho traçado por uma molécula conforme ela viaja em um líquido ou um gás, o caminho de um animal buscando alimento, comportamento de supercordas, o preço flutuante de ações e da situação financeira de um jogador pode ser aproximada por modelos de passeio aleatório, mesmo que eles possam não ser verdadeiramente aleatórios na realidade. Como ilustrado por esses exemplos, passeios aleatórios têm aplicações em muitas áreas científicas, incluindo ecologia, psicologia, ciência da computação, física, química, e biologia, e também para a economia. Os passeios aleatórios explicam os comportamentos observados em muitos processos desses campos, e, assim, serve como um modelo fundamental para o registro de atividades estocásticas. Como um aplicação matemática, o valor de pi pode ser aproximado pela utilização de passeios aleatórios no ambiente de modelagem.[1][2] O termo passeio aleatório foi introduzido pela primeira vez por Karl Pearson , em 1905.[3]
Vários tipos diferentes de passeios aleatórios são de interesse, que podem diferir em vários aspectos. O próprio termo geralmente se refere a uma categoria especial de cadeias de Markov ou processos de Markov, mas muitos processos dependentes do tempo são referidos como passeios aleatórios, com um modificador que indica suas propriedades específicas. Passeios aleatórios (de Markov ou não) também podem acontecer em uma variedade de espaços: os mais comumente estudados incluem gráficos, outros entre os números inteiros ou reais, no plano ou em espaços vetoriais de dimensões superiores, em superfícies curvas ou em dimensões superiores de campo riemaniano, e também em grupos finitos, finitamente gerados ou grupo de Lie. O parâmetro de tempo também pode ser alterado. No contexto mais simples, a caminhada é em tempo discreto, que é uma sequência de variáveis aleatórias indexadas pelos números naturais. No entanto, também é possível definir passeios aleatórios que levam seus passos em momentos aleatórios, e, nesse caso, a posição tem de ser definido para todos os tempos . Casos específicos ou limites de passeios aleatórios incluem voos de Lévy e modelos de difusão, tais como o movimento Browniano.
Passeios aleatórios são um tema fundamental na discussão de processos de Markov. O estudo matemático deles tem sido intenso. Várias propriedades, incluindo, mas não limitado a distribuições de dispersão, tempo de retorno, taxas de encontro, recorrência ou transitoriedade, foram introduzidas para quantificar o seu comportamento.
Definição[editar | editar código-fonte]
O passeio aleatório mais simples é um caminho construído de acordo as seguintes regras:
- Há um ponto de partida.
- A distância de um ponto no caminho até o próximo é constante.
- A direção de um ponto no caminho para o próximo é escolhido aleatoriamente, e nenhuma direção é mais provável do que outra.
Passeio aleatório em malha[editar | editar código-fonte]
Um modelo de passeio aleatório popular é o passeio aleatório em uma estrutura regular, onde a cada passo a localização salta para outro local de acordo com alguma distribuição de probabilidade. Em um passeio aleatório simples, a localização só pode saltar para locais vizinhos da rede, formando um caminho de rede. No passeio aleatório simétrico simples em uma rede localmente finita, as probabilidades do salto de localização para cada um de seus vizinhos imediatos são as mesmas. O melhor exemplo estudado é de passeio aleatório sobre o inteiro rede d-dimensional (às vezes chamado de treliça hipercúbica) .[4]
Passeio aleatório unidimensional[editar | editar código-fonte]
Um exemplo elementar de um passeio aleatório é o passeio aleatório na linha de número inteiro, , que começa em 0 e em cada etapa move +1 ou -1 com igual probabilidade.
Este percurso pode ser ilustrado como se segue. Um marcador é colocado no zero na linha de número e uma moeda honesta é lançada. Se der cara, o marcador é movido uma unidade para a direita. Se der coroa, o marcador é movido uma unidade para a esquerda. Após cinco jogos, o marcador pode agora estar em 1, -1, 3, -3, 5, ou -5. Com cinco lançamentos, três caras e duas coroas, em qualquer ordem, vai terminar em 1. Há 10 maneiras de resultar em 1 (lançando três caras e duas coroas), 10 maneiras de resultar em -1 (lançando três coroas e duas caras), 5 formas de resultar em 3 (lançando quatro caras e uma coroa), 5 formas de resultar em -3 (lançando quatro coroas e uma cara), uma forma de resultar em 5 (lançando cinco caras), e uma forma de resultar em -5 (lançando cinco coroas). Veja abaixo uma ilustração dos resultados possíveis de 5 lançamentos.




Para definir esta caminhada formalmente, toma-se variáveis aleatórias independentes , onde cada variável é +1 ou −1, com uma probabilidade de 50% para qualquer valor, e definir e . A série é chamada passeio aleatório simples em . Esta série (a soma da seqüência de −1 e +1) dá a distância percorrida, se cada parte do passeio é de comprimento 1. A expectativa de é zero. Isto é, a média de todos os lançamentos se aproxima de zero conforme o número de lançamentos aumenta. Isto segue pela propriedade da aditividade finita da expectativa:
Um cálculo semelhante, utilizando a independência de variáveis aleatórias e o fato de que , mostra que:
Isto sugere que , a distância esperada depois de n passos, deve ser da ordem de . De fato,[5]
Este resultado mostra que a difusão é ineficaz para a mistura devido à forma como a raiz quadrada funciona para grandes .
Quantas vezes um passeio aleatório atravessa uma linha de fronteira se for permitido continuar a caminhar para sempre? Um passeio aleatório simples em vai atravessar cada ponto um número infinito de vezes. Este resultado tem muitos nomes: o fenômeno da passagem de nível, recorrência ou o ruína do jogador. A razão para o último nome é o seguinte: um jogador com uma quantidade finita de dinheiro vai eventualmente perder ao jogar um jogo justo contra uma banca com uma quantidade infinita de dinheiro. O dinheiro do jogador irá realizar um passeio aleatório, e ele vai chegar a zero em algum ponto, e o jogo irá acabar.
Se a e b são números inteiros positivos, então o número esperado de passos até que um passeio aleatório unidimensional simples começando em 0 primeiro atingir b ou −a é ab. A probabilidade de que este passeio vai atingir b antes de −a é que pode ser derivado do fato de que o passeio aleatório simples é um martingale.
Alguns dos resultados mencionados acima podem ser derivados a partir de propriedades do triângulo de Pascal. O número de diferentes passeios de n passos, onde cada passo é +1 ou −1 é 2n. Para um passeio aleatório simples, cada um desses passeios são igualmente prováveis. Para que Sn ser igual a um número k , é necessário e suficiente que o número de passos +1 no passeio exceda o de −1 por k. O número de passeios que satisfazem é igual ao número de maneiras de escolher (n - k)/2, com n sendo o número de movimentos permitidos,[6] denotado . Para que isto tenha sentido, é necessário que n e k sejam números pares. Portanto, a probabilidade de que é igual a . Representando as entradas do triângulo de Pascal, em termos de fatoriais e usando a fórmula de Stirling, pode-se obter boas estimativas para estas probabilidades para valores grandes de .
Se o espaço é limitado para + para ser breve, o número de maneiras em que um passeio aleatório vai pousar em qualquer determinado número tendo ocorrido cinco lançamentos, pode ser mostrado como {0,5,0,4,0,1}.
Esta relação com o triângulo de Pascal é demonstrada para valores pequenos de n. Com zero lançamentos, a única possibilidade será a de permanecer em zero. No entanto, com um lançamento, há uma chance de resultar em −1, ou uma chance de resultar em 1. Com dois lançamentos, um marcador em 1 pode mover para 2 ou voltar para zero. Um marcador em −1, poderia mover para −2 ou de volta a zero. Portanto, há uma chance de resultar em −2, duas chances de terminar em zero, e uma chance de pouso em 2.
| k | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||||
| 1 | 1 | ||||||||||
| 1 | 2 | 1 | |||||||||
| 1 | 3 | 3 | 1 | ||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||
| 1 | 5 | 10 | 10 | 5 | 1 |
O teorema do limite central e a lei do logaritmo iterado descreve aspectos importantes do comportamento de passeios aleatórios simples em . Em particular, o primeiro implica que conforme n aumenta, as probabilidades (proporcional aos números em cada linha) se aproximam de uma distribuição normal.
Como uma generalização direta, pode-se considerar passeios aleatórios em reticulados (infinitas vezes cobrindo gráficos ao longo do finito gráficos). Na verdade, é possível estabelecer o teorema do limite central nesta definição.[7][8]
Cadeia de Markov[editar | editar código-fonte]
Um passeio aleatório unidimensional também pode ser visto como uma cadeia de Markov cujo espaço de estado é dado por números inteiros . Para algum número p satisfazendo , as probabilidades de transição (a probabilidade Pi,j de ocorrer um movimento a partir do estado i para o estado j) são dadas por .
Dimensões superiores[editar | editar código-fonte]

Em dimensões superiores, o conjunto de pontos caminhados aleatoriamente tem interessantes propriedades geométricas. Na verdade, obtém-se um fractal discreto, isto é, um conjunto que apresenta autossimilaridade estocástica em grandes escalas. Em escalas pequenas, pode-se observar a "irregularidade" resultante da grade em que o caminho é realizado. A trajetória de um passeio aleatório é o conjunto dos pontos visitados, considerado como um todo e ignorando quando o passeio chegou a cada ponto. Em uma dimensão, a trajetória é simplesmente todos os pontos entre a altura mínima e máxima que o caminho alcançou (ambos são, em média, na ordem de √n).
Para visualizar os casos de duas dimensões, pode-se imaginar uma pessoa andando aleatoriamente em torno de uma cidade. A cidade é efetivamente infinita e com calçadas dispostas em uma grade quadrada. Em cada cruzamento, a pessoa escolhe aleatoriamente uma das quatro rotas possíveis (incluindo a rota pela qual veio até aquele ponto). Formalmente, este é um passeio aleatório no conjunto de todos os pontos do plano com coordenadas nos inteiros.
Será que a pessoa voltará em algum momento ao ponto de partida original do passeio? Este é o equivalente bidimensional da passagem de nível, discutida acima. A pessoa quase certamente irá voltar ao ponto de partida em um passeio aleatório bidimensional, mas para 3 dimensões ou mais, a probabilidade de retorno à origem diminui à medida que o número de dimensões aumenta. Em 3 dimensões, a probabilidade diminui para cerca de 34%.[9]
Veja também[editar | editar código-fonte]
- Movimento browniano
- Lei do logaritmo iterado
- Voos de Lévy
- A hipótese de buscas por vôos de Lévy
- Caminho autoevitante
- Raiz unitária
Referências
- ↑ Wirth, E.; Szabó, G.; Czinkóczky, A. (8 de junho de 2016). «MEASURE LANDSCAPE DIVERSITY WITH LOGICAL SCOUT AGENTS». ISPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences (em English). XLI-B2: 491–495. ISSN 1682-1750. doi:10.5194/isprs-archives-xli-b2-491-2016
- ↑ Wirth E. (2015). Pi from agent border crossings by NetLogo package. Retrieved from Wolfram Library Archive: http://library.wolfram.com/infocenter/MathSource/9281/
- ↑ Pearson, K. (1905). The Problem of the Random Walk. Nature. 72, 294.
- ↑ Révész Pal, Random walk in random and non random environments, World Scientific, 1990
- ↑ http://mathworld.wolfram.com/RandomWalk1-Dimensional.html
- ↑ Edward A. Colding et al, Random walk models in biology, Journal of the Royal Society Interface, 2008
- ↑ M. Kotani, T. Sunada (2003). «Spectral geometry of crystal lattices». Contemporary. Math. 338: 271–305. doi:10.1090/conm/338/06077
- ↑ M. Kotani, T. Sunada (2006). «Large deviation and the tangent cone at infinity of a crystal lattice». Math. Z. 254: 837–870. doi:10.1007/s00209-006-0951-9
- ↑ Pólya's Random Walk Constants
Leitura adicional[editar | editar código-fonte]
- Aldous, David; Fill, Jim, Reversible Markov Chains and Random Walks on Graphs, http://stat-www.berkeley.edu/users/aldous/RWG/book.html
- Ben-Avraham D.; Havlin S., Diffusion and Reactions in Fractals and Disordered Systems, Cambridge University Press, 2000.
- Feller, William (1968), An Introduction to Probability Theory and its Applications (Volume 1). ISBN 0-471-25708-7
- Hughes, Barry D. (1996), Random Walks and Random Environments, Oxford University Press. ISBN 0-19-853789-1
- Mackenzie, Dana, "Taking the Measure of the Wildest Dance on Earth", Science, Vol. 290, 8 December 2000.
- Norris, James (1998), Markov Chains, Cambridge University Press. ISBN 0-521-63396-6
- Pólya G.(1921), "Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Strassennetz", Mathematische Annalen, 84(1-2):149–160, March 1921.
- Révész, Pal (2013), Random Walk in Random and Non-random Environments (Third Edition), World Scientific Pub Co. ISBN 978-981-4447-50-8
- Weiss G. Aspects and Applications of the Random Walk, North-Holland, 1994.
- Woess, Wolfgang (2000), Random Walks on Infinite Graphs and Groups, Cambridge tracts in mathematics 138, Cambridge University Press. ISBN 0-521-55292-3
- Toshikazu Sunada (2012), Topological Crystallography --With a View Towards Discrete Geometric Analysis--, Surveys and Tutorials in the Applied Mathematical Sciences, Vol. 6, Springer
Ligações externas[editar | editar código-fonte]
- Constantes de passeio aleatório de Pólya
- Passeio aleatório no Java Applet
- Passeio aleatório quântico
Categoria:Processos estocásticos Categoria:Mercado de capitais
























![{\displaystyle P[S_{0}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4fec1fd8784c3de7c8b113f7ff728db75c8f584)
![{\displaystyle 2P[S_{1}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c61317a7c5e847ee2756e0a746abee7bdd9da12)
![{\displaystyle 2^{2}P[S_{2}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca9583c3e61f6b6739502821af6cb79fae46f22e)
![{\displaystyle 2^{3}P[S_{3}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/283a77c450ba9f63e54a01a94fb9cec8e8ee07b8)
![{\displaystyle 2^{4}P[S_{4}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/208950bbe9ff3b0dd09b94b35dd390d3ddefea15)
![{\displaystyle 2^{5}P[S_{5}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b86e6675acd3df11dbd6fd80d3e1c0b10e3b6bf)


