Amostra (estatística)
| Estatística |
|---|
 |
Em estatística e metodologia da pesquisa quantitativa, uma amostra é um conjunto de dados coletados e/ou selecionados de uma população estatística por um procedimento definido.[1] Os elementos de uma amostra são conhecidos como pontos amostrais, unidades amostrais ou observações.
Tipicamente, a população é muito grande, portanto fazer um censo ou uma enumeração completa de todos os valores na população é pouco prático ou impossível.[2] A amostra geralmente representa um subconjunto de tamanho manejável.[3] Amostras são coletadas e estatísticas são calculadas a partir das amostras, de modo que se possam fazer inferências ou extrapolações da amostra à população.[4]
A amostra de dados pode ser retirada de uma população "sem reposição" (nenhum elemento pode ser selecionado mais de uma vez na mesma amostra), no caso em que a amostra é um subconjunto de uma população, ou "com reposição" (um elemento pode aparecer múltiplas vezes em uma amostra), no caso em que a amostra é um multisubconjunto.[5]
Tipos de amostra[editar | editar código-fonte]
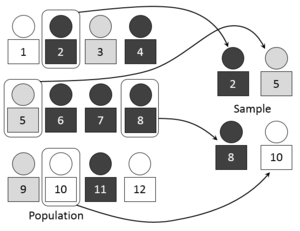
Uma amostra completa é um conjunto de objetos de uma população de origem que inclui todos os objetos que satisfazem um conjunto de critérios de seleção bem definidos.[6] Por exemplo, uma amostra completa de homens australianos com altura superior a dois metros consistiria em uma lista com todos os homens australianos com altura superior a dois metros. Contudo, não incluiria homens alemães, mulheres australianas altas ou pessoas com altura inferior a dois metros. Então, compilar tal amostra completa exige uma lista completa da população de origem, incluindo dados sobre altura, gênero e nacionalidade para cada membro da população de origem. No caso de populações humanas, é improvável que tal lista completa exista, já que a população humana está na casa dos bilhões. No entanto, tais amostras completas estão frequentemente disponíveis em outras disciplinas, como o conjunto de jogadores em uma divisão principal de esportes, as datas de nascimento dos membros de um parlamento ou uma lista de magnitude limitada completa de objetos astronômicos.
Uma amostra não viesada (representativa) é um conjunto de objetos escolhidos a partir de uma amostra completa usando um processo de seleção que não depende das propriedades dos objetos.[7] Por exemplo, uma amostra não viesada de homens australianos com altura superior a dois metros pode consistir em um subconjunto aleatoriamente amostrado de 1% dos homens australianos com altura superior a dois metros. Contudo, um subconjunto escolhido a partir do registro eleitoral pode ser viesada já que, por exemplo, homens com menos de 18 anos não estarão no registro eleitoral. No contexto astronômico, uma amostra não viesada pode consistir em uma fração de uma amostra completa para a qual os dados estão disponíveis, desde que a disponibilidade dos dados não seja viesada por propriedades individuais de fontes.
A melhor forma de evitar viés ou não representatividade é selecionar uma amostra aleatória, também conhecida como amostra probabilística. Uma amostra aleatória é definida como uma amostra em que cada membro individual da população tem um chance conhecida e diferente de zero de ser selecionado como parte da amostra.[8] Os vários tipos de amostras aleatórias incluem amostras aleatórias simples, amostras sistemáticas, amostras aleatórias estratificadas e amostras aleatórias por conglomerados.
Uma amostra que não é aleatória é chamada de amostra não aleatória ou amostra não probabilística.[9] Alguns exemplos de amostras não aleatórias incluem as amostras por conveniência, amostras por julgamento, amostras intencionais, amostras por quotas, amostras por bola de neve e nós de quadratura em métodos quase-Monte Carlo.
Amostragens probabilísticas[editar | editar código-fonte]
- Amostragem aleatória: É a amostra cuja formação precisou de um procedimento de seleção dos elementos ou grupo de elementos de modo que dá a cada elemento uma probabilidade de inclusão na amostra que seja calculável e diferente de zero.[10]
- Amostragem aleatória simples: É aquela em que toda amostra possível de mesmo tamanho tem a mesma chance de ser selecionada a partir da população.[11]
- Amostragem aleatória com reposição: É aquela em que os elementos da amostra podem se repetir, estando presente mais de uma vez na amostra, mesmo participando somente uma vez da população.
- Amostragem sistemática ou catastrófica: Consiste em um elemento aleatório, por exemplo, um nome a cada dez de uma lista, a décima peça produzida em uma linha de produção etc. Sua principal vantagem é sua simplicidade e flexibilidade, sendo mais fácil de instruir os trabalhadores de campo.[12]
- Amostragem estratificada: Consiste em dividir ou estratificar a população em um certo número de subpopulações que não se sobrepõem e então extrair uma amostra de cada estrato. Este tipo de amostragem também é usado quando métodos diferentes de coleta de dados são aplicados em diferentes partes da população.[13]
- Amostragem representativa: É a amostra da qual a análise pode oferecer conclusões válidas sobre a população, para tanto é preciso que a amostra seja extraída de acordo com critérios bem definidos.[14]
Amostragens não probabilísticas[editar | editar código-fonte]
As amostragens não probabilísticas servem para sondagens sem propósitos inferenciais, nestes casos, os processos que envolvem comparações estatísticas que usem cálculos científicos não são válidos. Os processos de amostragem não probabilísticos podem ser:[15]
- Amostragem de voluntários: É quando os próprios componentes da população se voluntariam para participar de uma pesquisa.
- Amostragem por bola de neve: Escolhem-se voluntários e estes indicam "conhecidos" com o mesmo perfil para responder entrevistas ou questionário e assim sucessivamente. Formam-se redes de referência.
- Amostragem por quotas: Consiste em buscar repetir a proporção de elementos de cada estrato da população, na amostragem por cotas os elementos da amostra não são selecionados através de sorteio.
- Amostragem por escolha racional: É quando o pesquisador busca na população uma parte dela que interessa, ou seja, os participantes são escolhidos por terem uma ou mais características específicas.
Descrição matemática da amostra aleatória[editar | editar código-fonte]
Em termos matemáticos, dada uma variável aleatória com distribuição , uma amostra aleatória de comprimento (em que pode ser qualquer um de ) é um conjunto de variáveis aleatórias independentes e identicamente distribuídas com distribuição .[16]
Uma amostra concretamente representa experimentos nos quais a mesma quantidade é medida. Por exemplo, se representa a altura de um indivíduo e indivíduos forem medidos, será a altura do -ésimo indivíduo. Note que a amostra de variáveis aleatórias (isto é, um conjunto de funções mensuráveis) não deve ser confundida com as realizações destas variáveis (que são os valores que estas variáveis aleatórias assumem, formalmente chamados de variados aleatórios). Em outras palavras, é uma função que representa a medição no -ésimo experimento e é o valor realmente obtido quando se faz o experimento.
O conceito de uma amostra assim inclui o processo pelo qual os dados são obtidos (isto é, as variáveis aleatórias). Isto é necessário de modo que afirmações matemáticas possam ser feitas sobre a amostra e as estatísticas computadas a partir dela, tais como a média e a covariância amostrais.
Ver também[editar | editar código-fonte]
Referências[editar | editar código-fonte]
- ↑ Roxy., Peck,; L., Devore, Jay (2008). Introduction to statistics and data analysis 3rd ed. Australia: Thomson Brooks/Cole. ISBN 0495557838. OCLC 152580422
- ↑ R., Spiegel, Murray; Alu., Srinivasan, R.; Correa,, Carmona, Sara Ianda (2004). Teoria e problemas de probabilidade e estatística 2 ed. Porto Alegre: Bookman. ISBN 9788536302973. OCLC 69939300
- ↑ MARCONI), MARCONI, M. de A. (MARINA DE ANDRADE (2010). Fundamentos de metodologia científica. 7. ed. São Paulo: Atlas. ISBN 9788522457588. OCLC 708360984
- ↑ D.,, Pinheiro, João Ismael; Coelho,, Gomes, Gastão; Da,, Cunha, Sonia Baptista; Ramírez,, Carvajal, Santiago. Estatística básica : a arte de trabalhar com dados. Rio de Janeiro: [s.n.] ISBN 9788535230307. OCLC 901457079
- ↑ Berstel, Jean; Séébold, Patrice (30 de agosto de 1993). «A characterization of Sturmian morphisms». Springer, Berlin, Heidelberg. Mathematical Foundations of Computer Science 1993. Lecture Notes in Computer Science (em inglês): 281–290. ISBN 3540571825. doi:10.1007/3-540-57182-5_20
- ↑ 1931-, Pratt, John W. (John Winsor),; Robert., Schlaifer, (1995). Introduction to statistical decision theory. Cambridge, Mass.: MIT Press. ISBN 0262161443. OCLC 44964037
- ↑ Hahs-Vaughn, Debbie L.; Lomax, Richard G. (19 de junho de 2013). An Introduction to Statistical Concepts: Third Edition (em inglês). [S.l.]: Routledge. ISBN 9781136490125
- ↑ 1909-1980., Cochran, William G. (William Gemmell), (1977). Sampling techniques 3d ed. New York: Wiley. ISBN 047116240X. OCLC 2799031
- ↑ Johan., Strydom, (2004). Introduction to marketing 3rd ed. Cape Town, South Africa: Juta. ISBN 9780702165115. OCLC 56981522
- ↑ Paulo Cesar Fulgencio. Glossario - Vade Mecum. Mauad Editora Ltda; ISBN 978-85-7478-218-8. p. 46.
- ↑ Ryan,thomas. Estatística Moderna para Engenharia. Elsevier Brasil; ISBN 978-85-352-5088-6. p. 4.
- ↑ DONALD COOPER; Pamela S. Schindler. Metodos de Pesquisa Em Administracao. Bookman; 2003. ISBN 978-85-363-0117-4. p. 163.
- ↑ DONALD COOPER; Pamela S. Schindler. Metodos de Pesquisa Em Administracao. Bookman; 2003. ISBN 978-85-363-0117-4. p. 164.
- ↑ SONIA BAPTISTA DA CUNHA; SANTIAGO CARVAJAL. Estatistica Basica - a Arte de Trabalhar com Dados. Campus; 2009. ISBN 978-85-352-3030-7. p. 4.
- ↑ Paulo Afonso Bracarense. Estatística Aplicada Às Ciências Sociais. IESDE BRASIL SA; ISBN 978-85-387-0959-6. p. 87–89.
- ↑ S., Wilks, (2013). Mathematical Statistics. [S.l.]: Read Books Ltd. ISBN 9781443725255. OCLC 936199307







