Notação de Voigt

Em matemática, a notação de Voigt ou forma de Voigt em álgebra multilinear é um modo de representar um tensor simétrico reduzindo sua ordem. Existem algumas poucas variantes e nomes associados com esta ideia, por exemplo notação de Mandel, notação de Mandel–Voigt e notação de Nye. A notação de Kelvin é uma atualização devida a Helbig de antigas ideias de Lord Kelvin. As diferenças aqui repousam em certos pesos associados à seleção de linhas e colunas do tensor. A nomenclatura varia de acordo com a tradição no campo de aplicação.

Por exemplo, um tensor simétrico 2×2 em notação matricial

${\boldsymbol {X}}=\left[{\begin{matrix}x_{11}&x_{12}\\x_{21}&x_{22}\end{matrix}}\right]$

tem somente três elementos distintos, os dois da diagonal principal e o último fora desta diagonal, pois se o tensor é simétrico então os elementos com índices 12 e 21 são obrigatoriamente iguais. Assim, X pode ser expresso como o vetor

$(x_{11},x_{22},x_{12})^{\mathrm {T} }$.

Como outro exemplo, o tensor tensão (em notação matricial) é expresso como

${\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\end{matrix}}\right]$

Na notação de Voigt é simplificado como o vetor de seis componentes

${\tilde {\sigma }}=(\sigma _{xx},\sigma _{yy},\sigma _{zz},\sigma _{yz},\sigma _{xz},\sigma _{xy})^{\mathrm {T} }\equiv (\sigma _{1},\sigma _{2},\sigma _{3},\sigma _{4},\sigma _{5},\sigma _{6})^{\mathrm {T} }.$

O tensor deformação, similar em natureza ao tensor tensão — ambos são tensores simétricos de segunda ordem —, é expresso em forma matricial como

${\boldsymbol {\epsilon }}=\left[{\begin{matrix}\epsilon _{xx}&\epsilon _{xy}&\epsilon _{xz}\\\epsilon _{yx}&\epsilon _{yy}&\epsilon _{yz}\\\epsilon _{zx}&\epsilon _{zy}&\epsilon _{zz}\end{matrix}}\right]$

Sua representação na notação de Voigt é

${\tilde {\epsilon }}=(\epsilon _{xx},\epsilon _{yy},\epsilon _{zz},2\epsilon _{yz},2\epsilon _{xz},2\epsilon _{xy})^{\mathrm {T} }\equiv (\epsilon _{1},\epsilon _{2},\epsilon _{3},\epsilon _{4},\epsilon _{5},\epsilon _{6})^{\mathrm {T} },$

sendo $\gamma _{xy}=2\epsilon _{xy}$, $\gamma _{yz}=2\epsilon _{yz}$ e $\gamma _{zx}=2\epsilon _{zx}$ as deformações cisalhantes de engenharia.

A grande vantagem em usar diferentes representações para tensões e deformações é que a invariância escalar

${\boldsymbol {\sigma }}\cdot {\boldsymbol {\epsilon }}=\sigma _{ij}\epsilon _{ij}={\tilde {\sigma }}\cdot {\tilde {\epsilon }}$

é preservada.

Da mesma forma, um tensor simétrico de quarta ordem pode ser reduzido a uma matriz 6×6.

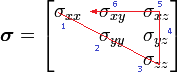
Regra mnemônica

Regra mnemónica fácil de memorizar a notação de Voigt para um tensor de segunda ordem 3×3:

• Escrever o tensor em forma matricial (no exemplo a seguir o tensor tensão)
• Eliminar a parte diagonal inferior
• Ponto de partida: Riscar a diagonal principal a partir do elemento de índices 11 (primeira linha e primeira coluna) ate o elemento de índice 33 (terceira linha e terceira coluna)
• Seguir riscando para cima até a primeira linha (da terceira até a primeira linha, permanecendo na terceira coluna)
• Retornar riscando até encontrar o último elemento não riscado da primeira linha (da terceira até a segunda coluna, permanecendo na primeira linha). Este é o ponto de chegada.

Os índices de Voigt são numerados em sequência a partir de 1, iniciando no ponto de partida e seguindo até o ponto de chegada (no exemplo os números em azul), mapeando todos os elementos do tensor.

Notação de Mandel

Para um tensor simétrico de segunda ordem

${\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{matrix}}\right]$

somente seis componentes são distintas, as três na diagonal principal e as outras três restantes fora da diagonal. Pode assim ser expresso na notação de Mandel como o vetor

${\tilde {\sigma }}^{M}=(\sigma _{11},\sigma _{22},\sigma _{33},{\sqrt {2}}\sigma _{12},{\sqrt {2}}\sigma _{23},{\sqrt {2}}\sigma _{13})^{\mathrm {T} }$

A principal vantagem da notação de Mandel é permitir o uso da mesma operação convencional usada com vetores, por exemplo

${\tilde {\sigma }}:{\tilde {\sigma }}={\tilde {\sigma }}^{M}\cdot {\tilde {\sigma }}^{M}=\sigma _{11}^{2}+\sigma _{22}^{2}+\sigma _{33}^{2}+2\sigma _{12}^{2}+2\sigma _{23}^{2}+2\sigma _{13}^{2}$

Um tensor simétrico de quarta ordem satisfazendo $D_{ijkl}=D_{jikl}$ e $D_{ijkl}=D_{ijlk}$ tem 81 componentes no espaço quadridimensional, mas somente 36 componentes são distintas. Assim, na notação de Mandel, pode ser expresso como

${\tilde {D}}^{M}={\begin{pmatrix}D_{1111}&D_{1122}&D_{1133}&{\sqrt {2}}D_{1112}&{\sqrt {2}}D_{1123}&{\sqrt {2}}D_{1113}\\D_{2211}&D_{2222}&D_{2233}&{\sqrt {2}}D_{2212}&{\sqrt {2}}D_{2223}&{\sqrt {2}}D_{2213}\\D_{3311}&D_{3322}&D_{3333}&{\sqrt {2}}D_{3312}&{\sqrt {2}}D_{3323}&{\sqrt {2}}D_{3313}\\{\sqrt {2}}D_{1211}&{\sqrt {2}}D_{1222}&{\sqrt {2}}D_{1233}&2D_{1212}&2D_{1223}&2D_{1213}\\{\sqrt {2}}D_{2311}&{\sqrt {2}}D_{2322}&{\sqrt {2}}D_{2333}&2D_{2312}&2D_{2323}&2D_{2313}\\{\sqrt {2}}D_{1311}&{\sqrt {2}}D_{1322}&{\sqrt {2}}D_{1333}&2D_{1312}&2D_{1323}&2D_{1313}\\\end{pmatrix}}$

Aplicações

Epônimo do físico Woldemar Voigt, é de uso prático em cálculos envolvendo modelos constitutivos para a simulação de materiais sólidos, tais como a lei de Hooke, bem como no método dos elementos finitos e MRI de difusão.

A lei de Hooke consiste em um tensor simétrico de quarta ordem, com 81 componentes (3×3×3×3), relacionando dois tensores simétricos de segunda ordem, os tensores tensão e deformação. A notação de Voigt permite que este tensor seja reduzido a uma matriz simétrica 6×6.

Bibliografia

• P. Helnwein (2001). Some Remarks on the Compressed Matrix Representation of Symmetric Second-Order and Fourth-Order Tensors. Computer Methods in Applied Mechanics and Engineering, 190(22–23):2753–2770

Ver também

• Lei de Hooke