Correlação
As referências deste artigo necessitam de formatação. (Outubro de 2022) |
- Este artigo abrange a correlação entre duas variáveis. O termo correlação pode também significar a relação invertida de duas funções ou a correlação eletrônica em sistemas moleculares.
Em probabilidade e estatística, correlação, dependência ou associação é qualquer relação estatística (causal ou não causal) entre duas variáveis[1] e correlação é qualquer relação dentro de uma ampla classe de relações estatísticas que envolva dependência entre duas variáveis.[2] Por exemplo, a correlação entre a estatura dos pais e a estatura dos pais e dos filhos. Embora seja comumente denotada como a medida de relação entre duas variáveis aleatórias,[2][3] correlação não implica causalidade.[4] Em alguns casos, correlação não identifica dependência entre as variáveis. Em geral, há pares de variáveis que apresentam forte dependência estatística, mas que possuem correlação nula. Para este casos, são utilizadas outras medidas de dependência.[5]
Informalmente correlação é sinônimo de dependência. Formalmente variáveis são dependentes se não satisfizerem a propriedade matemática da independência probabilística. Em termos técnicos, correlação refere–se a qualquer um dos vários tipos específicos de relação entre os valores médios. Existem diferentes coeficientes de correlação ( ou ) para medir o grau de correlação. Um dos coeficientes de correlação mais conhecidos é o coeficiente de correlação de Pearson, obtido pela divisão da covariância de duas variáveis pelo produto dos seus desvios padrão[6] e sensível a uma relação linear entre duas variáveis.[7] Entretanto, há outros coeficientes de correlação mais robustos que o coeficiente de correlação de Pearson. Isto é, mais sensíveis às relações não lineares.[8][9][10]
Histórico[editar | editar código-fonte]
Os conceitos de correlação e de regressão originaram—se nos anos de 1880 com Sir Francis Galton (1822 – 1911), de acordo com sua autobiografia Memories of My Life, publicada em 1890.[11] Em seus estudos sobre o diâmetro das sementes das ervilhas—de—cheiro, Galton chegou à equação de reversão à média:
,
em que são o diâmetro das sementes das plantas filhas, são o diâmetro das sementes das plantas pais e é a reversão (posteriormente, regressão). Em suas pesquisas sobre a comparação entre estaturas de pais e filhos, Galton usou o termo regressão pela primeira vez para denotar a regressão à média da população observada. Com base na análise da tábua de frequência bidimensional representada pelas alturas dos filhos adultos e meio—pais (média do pai e da mãe), Galton chegou à fórmula da superfície da representação gráfica (atualmente, a fórmula da função normal bidimensional) e à expressão da co—relação (atualmente, correlação) como conseqüência das variações devidas a causas comuns.[12]
O desenvolvimento da correlação, com a publicação de Natural Inheritance em 1889, marca o início do período moderno da estatística. A correlação prometia ser útil em muitos campos científicos, especialmente diante da necessidade de estabelecer diretrizes de causalidade. Entretanto, na época de Galton a disciplina de teoria estatística era não existia na Inglaterra (não havia curso universitário revistas especializadas sobre o assunto). Então, Galton percebeu que regressão e correlação poderiam ser o ponto de partida de uma nova disciplina, embora fosse preciso organizar as contribuições dispersas e estruturar o conhecimento de modo sistemático. Por volta de 1890, este contexto começou a chamar atenção de estatísticos e jovens cientistas como Edgeworth, Weldon e Pearson.[13]
Weldon e Pearson[editar | editar código-fonte]
A expressão de correlação foi modificada pelo professor de Zoologia em Cambridge Walter Frank Raphael Weldon (1860 – 1906), que incorporou o sinal positivo e o sinal negativo a partir da análise das dimensões de 22 pares de órgãos de várias espécies de camarões. Entretanto, a atual fórmula do coeficiente de correlação foi determinada em 1896 por Karl Pearson (1857 – 1936).[12] Em Mathematical Contributions to the Theory of Evolution, Pearson publicou entre 1893 e 1912 suas contribuições para a análise de regressão, o coeficiente de correlação e o teste qui—quadrado de significância estatística. Especialmente, o coeficiente de correlação produto—momento de Pearson com foi desenvolvido com base em um conjunto de dados sobre estatura de pais e filhos (inicialmente coletados por Galton), tornando—se a primeira medida de força de associação em estatística.[14]
Edgeworth[editar | editar código-fonte]
Em 1892, Francis Ysidro Edgeworth (1845 – 1926) publicou parte do seu trabalho sobre correlação em Philosophical Magazine com base nas contribuições prévias de Galton. Nos artigos Correlated Averages e The Law of Error and Correlated Averages, Edgeworth introduziu o termo coeficiente de correlação, forneceu a primeira análise matemática de correlação e mostrou sua relação com a distribuição multivariada normal. Entre 1893 e 1895, Edgeworth publicou a continuação do seu trabalho sobre correlação na Philosophical Magazine e na Journal of the Royal Statistcal Society. Por exemplo, o resumo de Recent Contributions to thew Theory of Statistics, que culminou em quatro importantes trabalhos Statistics on Unprogressive Communities, The Assymetrical Probability Curve, The Compound Law of Error e Supplementary Notes on Statistics.[15]
Correlação linear[editar | editar código-fonte]
Os diferentes setores da sociedade utilizam amostras de populações , em vez de populações de dados , para auxiliar nas análises dos objetivos das suas áreas de conhecimento. Isto ocorre porque um conjunto reduzido de dados () torna o processo mais econômico e mais rápido do ponto de vista matemático. Isto deve–se aos erros de arredondamentos dos cálculos que são feitos em estatística, considerando que uma grande quantidade de dados envolve mais cálculos que uma pequena quantidade de dados.[16]
Correlação populacional[editar | editar código-fonte]
A correlação populacional trata da medida da direção e do grau com que as variáveis e se associam linearmente em uma população. O coeficiente de correlação populacional entre duas variáveis e com valores esperados e e desvios padrão e é definido como:
em que é o operador do valor esperado, é a covariância e é uma notação alternativa para coeficiente de correlação.[17]
O coeficiente de correlação é simétrico: .[18]
O coeficiente de correlação de Pearson é +1 no caso de uma relação linear (correlação) direta perfeita (crescente), -1 no caso de uma relação linear (anticorrelação) decrescente perfeita (inversa) e qualquer valor no intervalo aberto (-1, 1) nos outros casos indicando o grau de dependência linear entre as variáveis.[19] É um corolário da desigualdade de Cauchy–Schwarz, em que a correlação não pode exceder 1 em valor absoluto. Quanto mais próximo de 0, mais fraca a correlação entre as variáveis (mais próximas de não correlacionados). Quando mais próximo de -1 ou +1, mais forte a correlação entre as variáveis.[20]
Se as variáveis forem independentes, o coeficiente de correlação de Pearson é 0. Entretanto, o contrário não é verdadeiro porque o coeficiente de correlação detecta apenas dependências lineares entre duas variáveis. Por exemplo, suponha–se que a variável aleatória é simetricamente distribuída em torno de 0 e que a variável aleatória . Então, é completamente determinada por , de modo que e são perfeitamente dependentes, mas a correlação entre elas é 0. Em outras palavras, as variáveis não são correlacionadas. Entretanto, no caso especial em que e são conjuntamente normais, não correlação é equivalente à independência.[17]
Correlação amostral[editar | editar código-fonte]
Coeficiente de correlação de Pearson[editar | editar código-fonte]
A correlação amostral trata da medida da direção e do grau com que as variáveis e se associam linearmente em uma amostra. Karl Pearson desenvolveu o coeficiente amostral a partir de uma ideia semelhante, porém ligeiramente diferente da de Francis Galton. Então, o coeficiente amostral pode ser chamado de coeficiente produto–momento de Pearson, coeficiente de correlação de Pearson ou simplesmente coeficiente de correlação, que é a medida mais conhecida de dependência entre duas variáveis quantitativa.[7]
Para uma série de medições de e , e para , o coeficiente de correlação da amostra pode ser usado para estimar o coeficiente de correlação de Pearson da população entre e . Então, o coeficiente de correlação da amostra é escrito como:
,
em que e são as médias amostrais de e .[6]
O coeficiente de correlação de Pearson é definido apenas se os desvios padrão e forem finitos e diferentes de zero. Isto também pode ser escrito como:
Se e são resultados de medições que contêm erros de medições, os limites realistas no coeficiente de correlação não são -1 para +1, mas um intervalo menor.[21]
No caso de um modelo linear com uma única variável independente, o coeficiente de determinação é o quadrado do coeficiente de correlação de Pearson .[22]
Propriedades de para variáveis e [editar | editar código-fonte]
- : relação linear perfeita e positiva
- : inexistência linear
- : relação linear perfeita e negativa
- : relação linear positiva
- : relação linear negativa
- Se os valores das variáveis e são convertidos para uma escala diferente, o valor de não é alterado
- O valor de não é afetado pela escolha das variáveis ou
- Permutando e , o valor de não é alterado
- Mede direção e o grau (intensidade) com que as variáveis e as quais se associam linearmente
- Não é útil para casos não-lineares[23]
Interpretação geométrica[editar | editar código-fonte]
As duas séries de valores e podem ser consideradas vetores em um espaço de dimensão . Com a substituição por vetores centrados nas médias, têm-se e .
O cosseno do ângulo entre os vetores e , usando a norma euclidiana e o produto escalar normalizado, é dado pela fórmula:[24]
,
Portanto, , em que está sempre -1 e 1.
O coeficiente de correlação é o cosseno do ângulo entre os dois vetores centrados:[24]
- Se , então e os dois vetores são colineares (paralelos);
- Se , então e os dois vetores são ortogonais;
- Se , então e os dois vetores são colineares, mas em direções opostas.
Mais genericamente, , em que é a função inversa do cosseno. representa, do ponto de vista geométrico, a intensidade da correlação entre os dois vetores aleatórios e , o que não pode ser medido em um teste de significância.[24]
Mais genericamente, , em que é o inverso da função cosseno. Do ponto de vista geométrico, não se fala em correlação linear. O coeficiente de correlação sempre tem um significado, independentemente do valor entre -1 e 1.
Correlação não linear[editar | editar código-fonte]
Coeficiente de correlação (ETA)[editar | editar código-fonte]
O coeficiente de correlação (ETA) ou razão de correlação mede a intensidade de associação entre variável dependente e independente para casos não–lineares. Isto é, trata a relação de uma variável quantitativa e outra variável categórica ou nominal . Expressa–se em percentagem. Assume valores entre 0 e 1.[25]
O coeficiente de correlação é dado pela expressão matemática:
Onde, é uma função. Ou seja, .[26]
Correlação de postos de Spearman[editar | editar código-fonte]
A correlação de postos de Spearman é utilizada para a relação entre dados não–lineares. Quando os dados de uma amostra são ordenados de forma crescente, obtém–se uma condição de ordem para que cada elemento ordenado seja um posto.
A correlação de postos de Spearman é dada pela expressão matemática:
,
em que , cm que e variando de 1 a , sendo a quantidade de elementos da amostra.[27]
Correlação de postos de Kendall[editar | editar código-fonte]
A correlação de postos de Kendall, também conhecido como de Kendall, é uma medida a partir de uma amostra de dados ordenados como a correlação de postos de Spearman. A vantagem de de Kendall é a generalização para um coeficiente de correlação parcial.
A correlação de Kendall é dada pela expressão matemática:
,
em que são os números de pares concordantes, são os números de pares discordantes e é a quantidade de elementos da amostra.[28]
Classificação dos coeficientes de correlação[editar | editar código-fonte]
Coeficientes de correlação como correlação de postos de Spearman e de Kendall medem a como uma variável aumenta enquanto outra variável também aumenta, sem exigir que o aumento seja representado por uma relação linear. Se, à medida que uma variável aumenta, uma outra variável diminui, os coeficientes de correlação de postos serão negativos. É comum considerar estes coeficientes de correlação de postos como alternativas ao coeficiente de correlação de Pearson, usado tanto para reduzir a quantidade de cálculo quanto para tornar o coeficiente menos sensível para distribuições não normais. Entretanto, esta visão tem pouca base matemática, na medida em que coeficientes de correlação de postos medem um tipo de relação diferente do coeficiente de correlação de Pearson e são melhor vistos como medidas de um tipo de associação diferente em vez de medidas alternativas do coeficiente de correlação da população.[29][30]
Para ilustrar a natureza dos coeficientes de correlação de postos, sejam os seguintes pares de números . De um par para outro, e aumentam. A relação é perfeita no sentido que o aumento de sempre é acompanhado do aumento de . Isto corresponde a uma correlação de posto perfeita e tanto a correlação de postos de Spearman quanto o de Kendall são iguais a 1, enquanto que o coeficiente de correlação de Pearson é igual a 0,7544, indicando que os pontos estão longe de cair em uma linha reta. Da mesma maneira, se sempre diminuir quando aumentar, o coeficiente de correlação de postos será -1 enquanto o coeficiente de correlação de Pearson poderá ou não poderá ser próximo de -1, dependendo do quão próximo os pontos estiverem de uma linha reta. Embora em casos extremos de correlação de posto perfeita ambos os coeficientes seja iguais (+1 ou -1), este geralmente não é o caso. Então, valores de dois coeficientes não podem ser comparados. Por exemplo, para os três pares a correlação de postos de Spearman é e o de Kendall é .[29]
Regressão linear[editar | editar código-fonte]
A regressão linear estuda a relação entre muitas ou poucas variáveis. A relação entre duas variáveis é chamada de regressão linear simples. A relação entre mais de duas variáveis é chamada de regressão linear múltipla.[31]
Regressão linear simples[editar | editar código-fonte]
A regressão linear simples estuda a relação entre uma variável independente e outra variável dependente , ambas quantitativas. A regressão linear resulta em uma equação sobre o comportamento das variáveis e :
,
em que é a variável resposta associada a –ésima observação de , é a –ésima observação do valor independente e fixado para a variável independente , é o erro aleatório para –ésima observação e, e são os parâmetros que precisam ser estimados.[32]
Por meio da correlação linear, encontra–se o gráfico de uma reta que possui as características de coeficiente angular e de coeficiente linear. Em termos matemáticos, a equação geral de uma reta é dada por , em que é o coeficiente angular e é o coeficiente linear. Como a regressão linear é uma equação de uma reta, em que é o coeficiente linear e o coeficiente angular para o mesmo grupo de dados amostrais, admite–se e . Portanto, encontrando–se uma correlação linear de uma amostra de dados, obtém–se a estimação dos parâmetros e para a regressão linear.[32]
Uma regressão linear é construída a partir de uma reta , determinada por uma correlação linear. Então, possui pontos cartesianos para determinar o coeficiente linear e o coeficiente angular para estabelecer os parâmetros e da regressão linear. Como e são observações amostrais e é o erro amostral, encontra–se o valor . Uma reta de regressão pode ser determinada somente com os valores e .[32]
Método dos mínimos quadrados[editar | editar código-fonte]
O cálculo do coeficiente de correlação entre duas variáveis é dado pelo ajuste linear. Para o cálculo das características da linha, o erro cometido ao representar a relação entre as variáveis precisa ser o menor possível. Embora não seja o único critério possível, na maioria das vezes minimiza–se a soma de todos os erros cometidos ao quadrado. Isto é chamado de ajuste para o método dos mínimos quadrados, que resulta na linha de regressão (quanto melhor a qualidade de representação da relação entre as variáveis pela linha de regressão, maior a associação do coeficiente de correlação linear).[33] O método dos mínimos quadrados é uma forma ágil para determinar os parâmetros desconhecidos para uma equação resultante de uma regressão linear, uma vez que minimiza a soma dos quadrados dos resíduos. O método dos mínimos quadrados é útil se os resíduos tiverem distribuição normal.[34]
Exemplos[editar | editar código-fonte]
Área comercial (correlação linear)[editar | editar código-fonte]
O setor comercial procura investir em propagandas para aumentar as vendas. Um gráfico de dispersão mostra se há uma correlação linear entre vendas e custo de propaganda. Supondo que uma empresa tem o cenário conforme a tabela abaixo.[35]

A partir do gráfico de dispersão da tabela acima, encontra–se uma correlação linear que mostra uma tendência entre investimento em propaganda e retorno positivo em vendas. É possível estimar um retorno de vendas com um aumento no custo em propaganda pelo cálculo matricial por meio da equação geral da reta , em que são os valores independentes que correspondem aos custos de propaganda e são os valores de retorno tratados para o cálculo do vetor chamado na tabela A de lucro sobre cada item. Esse cálculo é uma generalização método dos mínimos quadrados.[35]
Então,
A relação entre as variáveis é:
,
em que .
Realizando-se o cálculo entre as matrizes, obtém-se:
Portanto, com um investimento de 12 mil reais em propaganda no próximo mês, o lucro será de:
Área da saúde (correlação não linear)[editar | editar código-fonte]
Para se manter saudável, o consumo de água é indispensável. Uma gestora pública solicita à uma consultoria para verificar se há relação entre o consumo de água e a massa corporal de uma pessoa. A tabela B mostra indivíduos que fazem o consumo de água.[36]

Com a elaboração do diagrama de dispersão sobre a Tabela B, torna-se intuitivo pela plotagem (visualização) a não linearização entre massa e consumo de água. Embora necessárias, a intuição e a visualização não são suficientes para provar que não há relação linear. Dessa forma, o cálculo pelo coeficiente de Pearson facilita a demonstração da ausência de linearização para o objetivo da gestora pública. Para o cálculo é utilizado neste exemplo a segunda versão do coeficiente de Pearson, embora visualmente a fórmula seja mais extensa, ela é mais direta. Então,
Análise rápida sobre o cálculo
Neste exemplo, o coeficiente de Pearson tem o numerador igual a zero. Portanto, a razão é zero, o que significa inexistência linear. Em cálculo,
.[6]
A consultoria retorna a demonstração e a plotagem dos dados para a gestora pública que determina os planos de ações sobre o controle da reserva de água.[36]
Outras medidas de dependência entre variáveis[editar | editar código-fonte]
A informação fornecida por um coeficiente de correlação não é suficiente para definir a estrutura de dependência entre variáveis.[37] O coeficiente de correlação define completamente a estrutura de dependência apenas em casos particulares como uma distribuição normal multivariada. No caso de distribuições elípticas, caracteriza as (hiper)elipses de igual densidade. Entretanto, não caracteriza completamente a estrutura de dependência. Por exemplo, os graus de liberdade de uma distribuição t multivariada determinam o nível de dependência de cauda.[38]
Correlação da distância — Foi introduzida para endereçar a deficiência da correlação de Pearson que pode ser 0 para variáveis dependentes. Uma correlação de distância igual a 0 implica independência.[39][40]
Coeficiente de dependência randomizado — É uma medida baseada em cópula computacionalmente eficiente da dependência entre variáveis multivariadas. O coeficiente de dependência randomizado é invariante em relação a escalas não lineares de variáveis e é capaz de descobrir uma ampla variedade de padrões de associação funcionais e assume o valor 0 na independência.[21]
Proporção de correlação — É capaz de detectar praticamente qualquer dependência funcional.[41][42]
Informação mútua baseada na entropia / Correlação total / Correlação total dupla — São capazes de detectar ainda mais dependências gerais. Estas medidas de dependência às vezes são referidas como medidas de correlação de múltiplos momentos em comparação com aquelas medidas de dependência que consideram apenas a dependência do segundo momento (pairwise ou quadrática).[42]
Correlação policórica — É outra correlação aplicada a dados ordinais que buscam estimar a correlação entre as variáveis latentes teorizadas. Uma forma de capturar uma visão mais completa da estrutura de dependência é considerar uma cópula entre elas.[42]
Coeficiente de determinação — Generaliza o coeficiente de correlação para relações além da regressão linear simples.[43]
Sensibilidade à distribuição dos dados[editar | editar código-fonte]
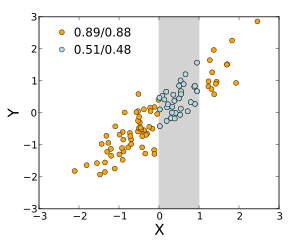
O grau de dependência entre as variáveis e não depende da escala, na qual as variáveis são expressas. Isto é, quando se analisa a relação entre e , a maior parte das medidas de correlação não são afetadas pela transformação de em e de em , em que são constantes (sendo positivos). Isto é verdade para algumas estatísticas de correlação, assim como para os análogos da sua população. Algumas estatísticas de correlação como o coeficiente de correlação de postos também são invariantes para transformações monótonas de distribuições marginais de e/ou .[44]
A maioria das medidas de correlação são sensíveis à maneira pela qual e são amostradas. As dependências tendem a ser mais fortes se vistas sobre uma variedade mais ampla de valores. Portanto, se for considerado o coeficiente de correlação entre as alturas dos pais e filhos entre todos os homens adultos e isto for comparado com o mesmo coeficiente de correlação calculado quando os pais selecionado têm entre 1,65m e 1,70m de altura, a correlação será mais fraca no último caso. Várias técnicas que foram desenvolvidas que tentam corrigir a restrição do intervalo em uma ou em ambas as variável são comumente usadas em metanálise. As equações do caso III e do caso II de Thorndike são as mais comuns.[45]
Várias medidas de correlação em uso podem ser indefinidas para certas distribuições conjuntas de e . Por exemplo, o coeficiente de correlação de Pearson é definido em termos de momentos. Portanto, será indefinido se os momentos também forem indefinidos. As medidas de dependência basedas em quantis são sempre definidas. As estatísticas baseadas em amostras que estimam as medidas populacionais de dependência podem ou não podem ter propriedades estatísticas desejáveis, como não ser viesada ou assintoticamente consistente, com base na estrutura espacial da população a partir da qual os dados foram amostrados.[carece de fontes]
A sensibilidade à distribuição dos dados tem uma vantagem. Por exemplo, a correlação em escala é designada para usar a sensibilidade ao intervalo para identificar correlações entre componentes rápidos de séries temporais. Reduzindo o intervalo de valores de maneira controlada, as correlações em uma longa escala de tempo são filtradas e apenas as correlações em uma curta escala de tempo são reveladas.[46]
Matrizes de correlação[editar | editar código-fonte]
A matriz de correlação de variáveis é a matriz , cujo -ésimo elemento da matriz é . Se as medidas de correlação usadas são coeficientes de produto—momento, a matriz de correlação é igual a matriz de covariância das variáveis padronizadas para . Isto é aplicado tanto para matriz de correlações populacionais (caso em que denota o desvio padrão populacional) quanto para matriz de correlações amostrais (caso em que denota o desvio padrão amostral). Consequentemente, cada uma é necessariamente uma matriz semidefinida—positiva. Além disso, a matriz de correlação é estritamente definida positiva se nenhuma variável puder ter todos os seus valores exatamente gerados como uma combinação linear dos outros. A matriz de correlação é simétrica porque a correlação entre e é igual a correlação entre e . Por exemplo, uma matriz de correlação aparece, por exemplo, na fórmula para o coeficiente de correlação múltipla (), uma medida de qualidade de ajuste em regressão múltipla: , onde é o vetor de correlações entre as variáveis independentes e a variável dependente e é a matriz de correlação.
Interpretação[editar | editar código-fonte]

| Correlação | Negativa | Positiva |
|---|---|---|
| Baixa | de -0,5 à 0 | de 0 à 0,5 |
| Alta | de -1 à -0,5 | de 0,5 à 1 |
É igual a 1, se uma das variáveis é uma função linear crescente da outra variável. É igual a -1, se uma variável é uma função decrescente. Os valores intermédios fornecem informações sobre o grau de dependência linear entre as duas variáveis.[19] Quanto mais próximo o coeficiente estiver dos valores extremos -1 e 1, mais forte é a correlação linear entre as variáveis.[20] Uma correlação igual a 0 significa que as variáveis não estão linearmente correlacionadas, mas podem estar correlacionado de forma não linear.[17]
O coeficiente de correlação não é sensível às unidades de cada variável. Por exemplo, o coeficiente de correlação linear entre a idade e o peso de uma pessoa será a mesma idade medida em semanas, meses ou anos. Entretanto, este coeficiente de correlação é extremamente sensível à presença de outliers no conjunto de dados (valores muito discrepantes, que podem ser considerados exceções).[47]
Vários autores propuseram diretrizes para a interpretação de um coeficiente de correlação. No entanto, Jacob Cohen observa que estes critérios são de certa forma arbitrários e não devem ser muito estritamente observados. A interpretação de um coeficiente de correlação depende do contexto e dos objetivos. Por exemplo, uma correlação de 0,9 pode ser considerada muito baixa se uma lei física for verificada utilizando ferramentas de qualidade, mas pode ser considerada muito alto nas ciências sociais em que pode haver uma maior presença de fatores complicadores.[48]
Dependência[editar | editar código-fonte]
É sempre possível calcular um coeficiente de correlação para variáveis (exceto para casos muito especiais), mas este coeficiente de correlação nem sempre é capaz de explicar a relação entre as variáveis.[49] Em uma tentativa de julgar a existência de uma relação linear entre duas variáveis, não é adequado julgar as correlações quando as relações entre elas não são lineares ou quando os dados são muito heterogêneos, uma vez que não há uma relação de causa e efeito entre as variáveis.[49] Se as duas variáveis aleatórias forem completamente independentes, então a correlação entre elas é nula. Entretanto, o inverso não necessariamente é verdadeiro, isto é, coeficiente de correlação nulo não não necessariamente implica independência entre as variáveis, pois se as variáveis apresentarem uma relação não linear (, por exemplo), o coeficiente de correlação será nulo, mesmo sendo relacionadas.[50] Estas considerações são ilustradas pelos seguintes exemplos no domínio de estatísticas:
 |
 |
 |
| MATRIZ DE CORRELAÇÃO | |||
|---|---|---|---|
| Estatura | Busto | Membro Superior | |
| Estatura | 1 | ||
| Busto | 0,85 | 1 | |
| Membro Superior | 0,55 | 0,63 | 1 |
Por exemplo, em antropometria são medidos para um certo número de indivíduos a estatura, a altura do busto e o comprimento do membro superior. Quanto maiores as medições, mais representativas são as correlações. Então, calculando por leis estatísticas a influência de algumas variáveis sobre outras, obtém–se a matriz ao lado (com valores fictícios).
- O valor 1 significa que as duas variáveis são exatamente correlacionadas. É o caso de uma relação linear entre as duas variáveis;
- O valor 0,85 significa que a estatura responde por 72,25% (0,85 × 0,85) do valor da altura do busto e assim por diante;
- A outra metade em falta da matriz pode ser completado por uma simetria ao longo da diagonal se as correlações forem reversíveis.
Precauções[editar | editar código-fonte]

Em geral, o estudo da relação entre as variáveis deve ser acompanhado de gráficos descritivos para a apreensão dos dados à disposição para evitar incorrer os limites estritamente técnicos dos cálculos utilizados.[51] Entretanto, quando se trata de se concentrar nas ligações entre diversas variáveis, as representações gráficas podem não ser possíveis ou podem não ter os dados dispersos de uma forma que seja imediatamente possível identificar a correlação. Os cálculos podem então ajudar a simplificar as interpretações possíveis sobre as ligações entre as variáveis e/ou indicarem as principais hipóteses necessárias para boas leituras.
Correlação e causalidade[editar | editar código-fonte]
A expressão correlação não implica causalidade significa que correlação não pode ser usada para a relação causal entre as variáveis. Por exemplo, a quantidade de queimaduras de sol pode estar fortemente correlacionada ao número de óculos de sol vendidos em uma cidade litorânea, mas nenhum fenômeno é provavelmente a causa do outro. Entretanto, por mais que a expressão não signifique que as correlações não podem indicar a potencial existência de relações causais, as causas subjacentes à correlação (se houver) podem ser indiretas e desconhecidas. Por exemplo, a correlação entre idade e altura em crianças é clara. No entanto, a correlação entre humor e saúde nas pessoas é menos óbvia. A afirmação correta é a melhora do humor leva à melhora da saúde, a boa saúde leva ao bom humor ou ambas? Em outras palavras, uma correlação pode ser tomada como evidência de uma possível relação causal, mas não pode indicar qual é a relação causal.[52]
Correlação e linearidade[editar | editar código-fonte]
IO coeficiente de correlação de Pearson indica a força de uma relação linear entre duas variáveis, mas seu valor geralmente não caracteriza completamente sua relação.[53] Em particular, se a média condicional de dado , denotado , não for linear em , o coeficiente de correlação não determinará completamente . A imagem ao lado mostra gráficos de dispersão do quarteto de Anscombe, um conjunto de quatro pares diferentes de variáveis criadas por Francis Anscombe. As quatro variáveis têm a mesma média (7,5), variância (4,12), correlação (0,816) e regressão linear.[54] Entretanto, a distribuição das variáveis é muito diferente. De acordo com os gráficos ao lado, o coeficiente de correlação como uma estatística de resumo não pode substituir a análise visual dos dados. Nota–se que os exemplos às vezes indicam que o coeficiente de correlação de Pearson presume que os dados seguem uma distribuição normal. No entanto, isto não é verdade.[55]
Ver também[editar | editar código-fonte]
- Autocorrelação
- Biometria
- Cópula (estatística)
- Correlação espúria
- Covariância
- Econometria
- Estatística
- Lambda de Goodman e Kruskal
- R²
- Relação cruzada
- Regressão
- Regressão espúria
Referências
- ↑ Bussab, Wilton de O.; Morettin, Pedro A. (2010). Estatística Básica 6ª ed. [S.l.]: Saraiva. p. 73. 540 páginas
- ↑ a b Bussab, Wilton de O.; Morettin, Pedro A. (2010). Estatística Básica 6ª ed. [S.l.]: Saraiva. p. 76. 540 páginas
- ↑ Mann, Prem S. (2010). Introdutory Statistics 7ª ed. [S.l.]: John Wiley & Sons. p. 592 — 593. 625 páginas
- ↑ Cooper, Donald R.; Schindler, Pamela S. (2016). Métodos de Pesquisa em Administração 12ª ed. [S.l.]: AMGH. p. 480. 695 páginas
- ↑ Bussab, Wilton de O.; Morettin, Pedro A. (2010). Estatística Básica 6ª ed. [S.l.]: Saraiva. p. 83 — 84. 540 páginas
- ↑ a b c d e Martins, Maria Eugénia Graça (2014). «Coeficiente de Correlação Amostral» (PDF). Revista de Ciência Elementar. p. 1. Consultado em 19 de maio de 2017
- ↑ a b Rodgers, J. L.; Nicewander, W. A. (1988). «Thirteen ways to look at the correlation coefficient». The American Statistician. 42 (1): 59–66. JSTOR 2685263. doi:10.1080/00031305.1988.10475524
- ↑ Croxton, Frederick Emory; Cowden, Dudley Johnstone; Klein, Sidney (1968) Applied General Statistics, Pitman. ISBN 9780273403159 (page 625)
- ↑ Dietrich, Cornelius Frank (1991) Uncertainty, Calibration and Probability: The Statistics of Scientific and Industrial Measurement 2nd Edition, A. Higler. ISBN 9780750300605 (Page 331)
- ↑ Aitken, Alexander Craig (1957) Statistical Mathematics 8th Edition. Oliver & Boyd. ISBN 9780050013007 (Page 95)
- ↑ Dodge, Yadolah (2008). The Concise Encyclopedia of Statistics. [S.l.]: Springer. p. 115 — 119
- ↑ a b Memória, José Maria Pompeu (2004). «Breve História da Estatística» (PDF): 22 — 25
- ↑ Piovani, PIJuan Ignacio (2013). «De Objeto a Método: Notas Históricas sobre Estatística e Pesquisa Social» (PDF). Sociologia & Antropologia. 3 (5): 245 — 270
- ↑ Caire, Elaine (2013). «A História da Curva Normal» (PDF): 27 — 30
- ↑ Barbe, Lluis (2010). Francis Ysidro Edgeworth: A Portrait with Family and Friends. [S.l.]: Edward Elgar. p. 169 — 171. 291 páginas
- ↑ «POPULAÇÃO E AMOSTRA» (PDF). Centro Universitário de Volta Redonda. p. 1. Consultado em 19 de maio de 2017
- ↑ a b c Razdolsky, Leo (2014). Probability—Based Structural Fire Load. [S.l.]: Cambridge University Press. p. 63. 335 páginas
- ↑ «Covariance and Correlation». Rice University. Consultado em 1 de junho de 2017
- ↑ a b Dowdy, S. and Wearden, S. (1983). "Statistics for Research", Wiley. ISBN 0-471-08602-9 pp 230
- ↑ a b Hirsch, Robert P. (2016). Introduction to Biostatistical Applications in Health Research with Microsoft Office Excel. [S.l.]: Wiley. p. 150. 392 páginas
- ↑ a b Lopez-Paz D. and Hennig P. and Schölkopf B. (2013). "The Randomized Dependence Coefficient", "Conference on Neural Information Processing Systems" Reprint
- ↑ Dogde, Yadolah (2008). The Concise Encyclopedia of Statistics. [S.l.]: Springer. p. 88 — 91
- ↑ Rodrigues, Lígia Henriques (18 de maio de 2015). «Regressão Linear Simples» (PDF). IMEUSP. p. 7. Consultado em 19 de maio de 2017
- ↑ a b c Gniazdowski, Zenon (2013). «Geometric interpretation of a correlation» (PDF). Zeszyty Naukowe Warszawskiej Wyższej Szkoły Informatyki. 7 (9): 27-35. Consultado em 8 de junho de 2017
- ↑ Shaldehi, Ahmad Hedayatpanah (2013). «Using Eta correlation ratio in analyzing strongly nonlinear relationship between two Variables in Practical researches» (PDF). Journal of mathematics and computer science. p. 2. Consultado em 19 de maio de 2017
- ↑ LEWANDOWSKI, DANIEL; COOKE, ROGER M.; TEBBENS, RADBOUD J. DUINTJER (2007). «Sample–based Estimation of Correlation Ratio with Polynomial Approximation» (PDF). Semantic Scholar. Consultado em 14 de junho de 2017
- ↑ Pontes, Antonio Carlos Fonseca. «ENSINO DA CORRELAÇÃO DE POSTOS NO ENSINO MÉDIO» (PDF). Universidade Federal do Acre. Consultado em 19 de maio de 2017
- ↑ Falcão, António Jorge Teixeira (2012). «Detecção de Correlação e Causalidade em Séries Temporais não Categóricas» (PDF). Universidade nova de Lisboa. Consultado em 19 de maio de 2017
- ↑ a b Yule, G.U and Kendall, M.G. (1950), "An Introduction to the Theory of Statistics", 14th Edition (5th Impression 1968). Charles Griffin & Co. pp 258–270
- ↑ Kendall, M. G. (1955) "Rank Correlation Methods", Charles Griffin & Co.
- ↑ Devore, Jay L. (2006). Probabilidade e Estatística para Engenharia e Ciências. [S.l.]: Cengage Learning. p. 432 — 433. 692 páginas
- ↑ a b c Filho, Luiz Medeiros de Araujo Lima. «Correlação e Regressão» (PDF). UNIVERSIDADE FEDERAL DA PARAÍBA. p. 6. Consultado em 19 de maio de 2017
- ↑ Viali, Lorí. «Estatística Básica» (PDF). Pontifícia Universidade Católica do Rio Grande do Sul (PUC–RS). Consultado em 7 de junho de 2017
- ↑ Filho, Kepler de Souza Oliveira (10 de abril de 2013). «Mínimos Quadrados». Universidade Federal do Rio Grande do Sul. p. 1. Consultado em 22 de maio de 2017
- ↑ a b Farber, Larson (2010). Estatística Aplicada. São Paulo: Pearson. 396 páginas. ISBN 978-85-7605-372-9
- ↑ a b Farber, Larson (2010). Estatística Aplicada. São Paulo: Pearson. 396 páginas. ISBN 9788576053729
- ↑ Mahdavi Damghani B. (2013). «The Non-Misleading Value of Inferred Correlation: An Introduction to the Cointelation Model». Wilmott Magazine. doi:10.1002/wilm.10252
- ↑ Abbara, Omar M. F. (2009). «Modelagem de Dependência em Séries Financeiras Multivariadas» (PDF). Campinas: Instituto de Matemática, Estatística e Computação Científica - Unicamp. p. 18. Consultado em 14 de junho de 2017
- ↑ Székely, G. J. Rizzo; Bakirov, N. K. (2007). «Measuring and testing independence by correlation of distances». Annals of Statistics. 35 (6): 2769–2794. doi:10.1214/009053607000000505
- ↑ Székely, G. J.; Rizzo, M. L. (2009). «Brownian distance covariance». Annals of Applied Statistics. 3 (4): 1233–1303. doi:10.1214/09-AOAS312
- ↑ Plischke, Elmar (2010). «An Adaptive Correlation Ratio Method» (PDF). Procedia Social and Behavioral Sciences: 7722 – 7723
- ↑ a b c Cao, Longbing (2015). «Coupling learning of complex interactions» (PDF). Information Processing and Management: 167 – 186. Arquivado do original (PDF) em 5 de julho de 2017
- ↑ «19. Simple Linear Regression IV — The Coefficient of Determination R²» (PDF). Leonard N. Stern School of Business — New York University. Consultado em 7 de junho de 2017
- ↑ Komenda, Stanislav (1993). «"Dressing up" with correlation» (PDF). Information Bulletin of Czech Statistical Society. 4. Consultado em 8 de junho de 2017
- ↑ Thorndike, Robert Ladd (1947). Research problems and techniques (Report No. 3). Washington DC: US Govt. print. off.
- ↑ Nikolić, D; Muresan, RC; Feng, W; Singer, W (2012). «Scaled correlation analysis: a better way to compute a cross-correlogram». European Journal of Neuroscience: 1–21. doi:10.1111/j.1460-9568.2011.07987.x
- ↑ «Chapter 14: Describing Relationships: Scatterplots and Correlation» (PDF). Wayne State University. Consultado em 7 de junho de 2017
- ↑ Jacob Cohen. (1988). Statistical power analysis for the behavioral sciences (2nd ed.)
- ↑ a b Agarwal, B.L. (2006). Basics Statistics 4 ed. Delhi: New Age International Publishers. p. 396. ISBN 81-224-1814-7
- ↑ Garlick, Andy. Estimating Risk: A Management Approach. [S.l.]: Gower. p. 187. ISBN 9780566087769
- ↑ Paiva, Delhi; Lauretto, Marcelo de Souza (2011). «Análise Exploratória de Dados». SIN5008 - Estatística computacional. Consultado em 14 de junho de 2017
- ↑ Aldrich, John (1995). «Correlations Genuine and Spurious in Pearson and Yule». Statistical Science. 10 (4): 364–376. JSTOR 2246135. doi:10.1214/ss/1177009870
- ↑ Mahdavi Damghani, Babak (2012). «The Misleading Value of Measured Correlation». Wilmott. 2012 (1): 64–73. doi:10.1002/wilm.10167
- ↑ Anscombe, Francis J. (1973). «Graphs in statistical analysis». The American Statistician. 27: 17–21. JSTOR 2682899. doi:10.2307/2682899
- ↑ Erro de citação: Etiqueta
<ref>inválida; não foi fornecido texto para as refs de nomethirteenways2
Leitura adicional[editar | editar código-fonte]
- COHEN, Jacob et al. Applied multiple regression/correlation analysis for the behavioral sciences. Routledge, 2013.
- ZANIBONI, GUSTAVO TADEU et al. Fusao bayesiana de imagens utilizando coeficientes de correlaçao localmente adaptáveis. Anais do IX SBSR. Santos, SP, 1998.
Ligações externas[editar | editar código-fonte]
- Correlation Comparison
- Finding Order in Randomness: Correlation
- Interpretação do Coeficiente de Correlação
- Interpreting Correlations
- Pearson's Correlation Coefficient
- Understanding Correlation
- Weighted Correlation Matrix
- Correlation (in statistics). A.V. Prokhorov (originator), Encyclopedia of Mathematics.
- Weisstein, Eric W. Correlation Coefficient. From MathWorld--A Wolfram Web Resource.
















![{\displaystyle \rho _{X,Y}\equiv \mathrm {corr} (x,y)={\mathrm {cov} (X,Y) \over \sigma _{X}\sigma _{Y}}={E[(X-\mu _{X})(Y-\mu _{Y})] \over \sigma _{X}\sigma _{Y}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72447aa4c39e6628a85d79a065209d294ecf6a5e)






























































































