Método dos mínimos quadrados
O Método dos Mínimos Quadrados (MMQ), ou Mínimos Quadrados Ordinários (MQO) ou OLS (do inglês Ordinary Least Squares) é uma técnica de otimização matemática que procura encontrar o melhor ajuste para um conjunto de dados tentando minimizar a soma dos quadrados das diferenças entre o valor estimado e os dados observados (tais diferenças são chamadas resíduos).[1]
É a forma de estimação mais amplamente utilizada na econometria. Consiste em um estimador que minimiza a soma dos quadrados dos resíduos da regressão, de forma a maximizar o grau de ajuste do modelo aos dados observados.
Um requisito para o método dos mínimos quadrados é que o fator imprevisível (erro) seja distribuído aleatoriamente e essa distribuição seja normal. O Teorema Gauss-Markov garante (embora indiretamente) que o estimador de mínimos quadrados é o estimador não-enviesado de mínima variância linear na variável resposta.
Outro requisito é que o modelo é linear nos parâmetros, ou seja, as variáveis apresentam uma relação linear entre si. Caso contrário, deveria ser usado um modelo de regressão não-linear.
Credita-se Carl Friedrich Gauss como o desenvolvedor das bases fundamentais do método dos mínimos quadrados, em 1795, quando Gauss tinha apenas dezoito anos. Entretanto, Adrien-Marie Legendre foi o primeiro a publicar o método em 1805, em seu Nouvelles méthodes pour la détermination des orbites des comètes. Gauss publicou suas conclusões apenas em 1809.[2][3][4]
História[editar | editar código-fonte]
Fundação[editar | editar código-fonte]
O método dos mínimos quadrados mostrou -se dos campos da astronomia e geodésia , à medida que cientistas e matemáticos procuravam proporcionar soluções para os desafios de navegar nos oceanos da Terra durante a Era da Exploração . A descrição precisa do comportamento dos corpos celestes era a chave para permitir que os navios navegassem em mar aberto, onde os marinheiros não podiam mais depender de avistamentos em terra para navegação.
O método foi o culminar de vários avanços ocorridos ao longo do século XVIII:
· A combinação de diferentes observações como sendo a melhor estimativa do valor verdadeiro; os erros diminuem com a agregação em vez de aumentar, talvez expressos pela primeira vez por Roger Cotes em 1722.
· A combinação de diferentes observações feitas nas mesmas condições, ao contrário de simplesmente tentar o melhor para observar e registrar uma única observação com precisão. A abordagem era conhecida como método das médias. Esta abordagem foi usada notavelmente por Tobias Mayer enquanto estudava as librações da lua em 1750, e por Pierre-Simon Laplace em seu trabalho para explicar as diferenças no movimento de Júpiter e Saturno em 1788.
· A combinação de diferentes observações feitas em diferentes condições. O método veio a ser conhecido como o método do menor desvio absoluto. Foi notadamente realizado por Roger Joseph Boscovich em seu trabalho sobre a forma da Terra em 1757 e por Pierre-Simon Laplace para o mesmo problema em 1799.
· O desenvolvimento de um critério que pode ser avaliado para determinar quando a solução com o erro mínimo foi alcançada. Laplace tentou especificar uma forma matemática da densidade de probabilidade dos erros e definir um método de estimativa que minimiza o erro de estimativa. Para este propósito, Laplace usou uma distribuição exponencial bilateral simétrica que agora chamamos de distribuição de Laplace para modelar a distribuição do erro, e usou a soma dos desvios absolutos como erro de estimativa. Ele achava que essas eram as suposições mais simples que poderia fazer e esperava obter a média aritmética como a melhor estimativa. Em vez disso, seu estimador foi a mediana posterior.
O método[editar | editar código-fonte]
A primeira exposição clara e concisa do método dos mínimos quadrados foi publicada por Legendre em 1805. A técnica é descrita como um procedimento algébrico para ajustar equações lineares aos dados e Legendre demonstra o novo método analisando os mesmos dados que Laplace para a forma da terra. O valor do método dos mínimos quadrados de Legendre foi imediatamente reconhecido pelos principais astrônomos e geodesistas da época. [ citação necessária ]
Em 1809, Carl Friedrich Gauss publicou seu método de cálculo das órbitas dos corpos celestes. Naquela obra, ele afirmou ter possuído o método dos mínimos quadrados desde 1795. Isso naturalmente levou a uma disputa de prioridade com Legendre. No entanto, para crédito de Gauss, ele foi além de Legendre e conseguiu conectar o método dos mínimos quadrados aos princípios da probabilidade e à distribuição normal . Ele conseguiu completar o programa de Laplace de especificar uma forma matemática da densidade de probabilidade para as observações, dependendo de um número finito de parâmetros desconhecidos, e definir um método de estimativa que minimiza o erro de estimativa. Gauss mostrou que a média aritméticaé de fato a melhor estimativa do parâmetro de localização, alterando a densidade de probabilidade e o método de estimativa. Ele então mudou o problema perguntando que forma a densidade deveria ter e que método de estimativa deveria ser usado para obter a média aritmética como estimativa do parâmetro de localização. Nessa tentativa, ele inventou a distribuição normal.
Uma das primeiras demonstrações da força do método de Gauss veio quando ele foi usado para prever a localização futura do recém-descoberto asteróide Ceres . Em 1 de janeiro de 1801, o astrônomo italiano Giuseppe Piazzi descobriu Ceres e foi capaz de rastrear seu caminho por 40 dias antes que se perdesse no brilho do sol. Com base nesses dados, os astrônomos desejavam determinar a localização de Ceres depois que ela emergiu atrás do sol, sem resolver as complicadas equações não lineares de Kepler do movimento planetário. As únicas previsões que permitiram com sucesso ao astrônomo húngaro Franz Xaver von Zach realocar Ceres foram aquelas realizadas por Gauss, de 24 anos, usando análise de mínimos quadrados.
Em 1810, depois de ler o trabalho de Gauss, Laplace, depois de provar o teorema do limite central , usou-o para dar uma grande amostra de justificação para o método dos mínimos quadrados e da distribuição normal. Em 1822, Gauss foi capaz de afirmar que a abordagem de mínimos quadrados para análise de regressão é ótima no sentido de que em um modelo linear onde os erros têm uma média de zero, não são correlacionados e têm variâncias iguais, o melhor estimador linear imparcial de os coeficientes é o estimador de mínimos quadrados. Este resultado é conhecido como teorema de Gauss-Markov .
O conceito da análise de mínimos quadrados também foi formulada de forma independente pelo americano Robert Adrain em 1808. Nos dois séculos posteriores, os pesquisadores da teoria dos erros e da estatística encontraram muitas maneiras diferentes de implementar os mínimos quadrado
Demonstração do Problema[editar | editar código-fonte]
O objetivo desse método consiste em ajustar os parâmetros de uma função modelo para que ela se ajuste melhor à um conjunto de dados. Um conjunto de dados simples consiste em n pontos (pares ordenados) , i = 1, ..., n, onde é uma variável independente e é uma variável dependente cujo valor é encontrado por observação.
A função modelo tem fórmula , onde m parâmetros ajustáveis são mantidos no vetor β. O objetivo é encontrar os valores dos parâmentros para o modelo que "melhor" se ajusta aos dados.
O ajuste do modelo é feito por seu resíduo, definido como a diferênça entre o valor real da variável dependente e o valor predito pelo modelo:

O método dos quadrados mínimos, então, encontra os valores dos parâmentros ideiais, minimizando a soma , dos quadrados residuais:
Um exemplo de modelo em duas dimensões é o da linha reta. Denotando a intercepção em y como e a inclinação como , a função do modelo é dada por:
Pode ocorrer de um conjunto de dados possuir mais de uma variável independente. Por exemplo, ao ajustar um plano a um conjunto de medidas de alturas, o plano é função de duas variáveis independentes, e , digamos. No caso mais geral, pode haver uma ou mais variáveis independentes e uma ou mais variáveis dependentes em cada par ordenado.
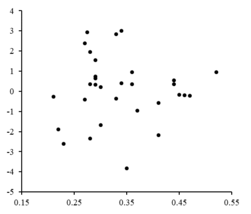
No Gráfico 1 está representado um gráfico residual ilustrando flutuações aleatóreas sobre , indicando que o modelo linear é apopriado, onde é uma variável independente e aleatória.
Se os pontos residuais tivessem algum tipo de forma e não estivessem flutuando aleatoriamente, um modelo linear não seria apropriado. Por exemplo, se o gráfico residual tivesse uma forma parabólica, conforme visto no Gráfico 2, um modelo parabólico seria mais apropriado para o conjunto.
Os resíduos para um modelo parabólico podem ser calculados pela fórmula
Regressão simples[editar | editar código-fonte]
Queremos estimar valores de determinada variável . Para isso, consideramos os valores de outra variável que acreditamos ter poder de explicação sobre conforme a fórmula:
onde:
- : Parâmetro do modelo chamado de constante (porque não depende de ).
- : Parâmetro do modelo chamado de coeficiente da variável .
- : Erro - representa a variação de que não é explicada pelo modelo.
Também temos uma base de dados com valores observados de e de . Perceba que, usando a base de dados, e são vetores, ou seja, representam uma lista de valores, um para cada observação da base de dados. O método dos mínimos quadrados ajuda a encontrar as estimativas de e . Como o nome diz, serão somente estimativas desses parâmetros, porque o valor real dos parâmetros são desconhecidos. Portanto, ao fazer a estimativa, mudamos a notação de algumas variáveis:
Deste modo, ao estimar o modelo usando a base de dados, estamos estimando, na verdade:
onde indica cada uma das observações da base de dados e passa a ser chamado de resíduo, ao invés de erro. Em alguns livros, a notação para as estimativas dos parâmetros é um pouco diferente. Ao invés de substituir a letra, apenas adiciona-se o símbolo chapéu ().
O método dos mínimos quadrados minimiza a soma dos quadrado dos resíduos, ou seja, minimiza .
A ideia por trás dessa técnica é que, minimizando a soma do quadrado dos resíduos, encontraremos e que trarão a menor diferença entre a previsão de e o realmente observado.
Substituindo por , temos:
A minimização se dá ao derivar em relação a e utilizando a regra da cadeia e então igualar a zero:
Distribuindo e dividindo a primeira expressão por temos:
onde é a média amostral de e é a média amostral de .
Substituindo esse resultado na segunda expressão temos:
Alguns livros também usam uma fórmula diferente que gera o mesmo resultado:
Exemplo de regressão simples[editar | editar código-fonte]

Considere a seguinte base de dados:
Consumo |
Renda | |
|---|---|---|
| 1 | 122 | 139 |
| 2 | 114 | 126 |
| 3 | 86 | 90 |
| 4 | 134 | 144 |
| 5 | 146 | 163 |
| 6 | 107 | 136 |
| 7 | 68 | 61 |
| 8 | 117 | 62 |
| 9 | 71 | 41 |
| 10 | 98 | 120 |
Aplicando as fórmulas acima, chega-se em:
portanto,
Interpretação: Tirando a parte do Consumo que não é influenciada pela Renda, o incremento de $ 1 na Renda causa um incremento esperado de $ 0,4954 no Consumo.
Regressão múltipla[editar | editar código-fonte]
A regressão múltipla apresenta um funcionamento parecido com o da regressão simples, porém, leva em consideração diversas variáveis explicativas influenciando ao mesmo tempo:
Ao usar a base de dados com variáveis explicativas e observações, o modelo pode ser escrito na forma matricial:
, onde representa o valor da -ésima variável da -ésima observação. A fórmula também pode ser escrita na forma resumida:
A solução de mínimos quadrados continua sendo alcançada através da minimização da soma do quadrado dos resíduos , que pode ser reescrito como , onde o apóstrofe significa que a matriz foi transposta.
Substituindo por , temos:
A minimização pode ser obtida ao derivar em relação a e igualar a zero. O primeiro termo não depende de , os segundo e terceiro termos são iguais e o quarto termo é uma forma quadrática dos elementos de .
Exemplo de regressão múltipla[editar | editar código-fonte]
Considere a base de dados usada no exemplo da regressão simples, porém, acrescente mais uma variável explicativa (taxa de juros):
Consumo |
Renda |
Taxa de Juros | |
|---|---|---|---|
| 1 | 122 | 139 | 11,5% |
| 2 | 114 | 126 | 12,0% |
| 3 | 86 | 90 | 10,5% |
| 4 | 134 | 144 | 9,0% |
| 5 | 146 | 163 | 10,0% |
| 6 | 107 | 136 | 12,0% |
| 7 | 68 | 61 | 10,5% |
| 8 | 117 | 62 | 8,0% |
| 9 | 71 | 41 | 10,0% |
| 10 | 98 | 120 | 11,5% |
Aplicando a fórmula acima, chega-se a:
portanto,
Interpretação: Tirando a parte do Consumo que não é influenciada pela Taxa de Juros, o incremento de $ 1 na Renda causa um incremento esperado de $ 0,6136 no Consumo; além disso, o incremento de 1 ponto percentual (0,01) na Taxa de Juros causa um decréscimo esperado de $ 10,3441 no Consumo.
Premissas[editar | editar código-fonte]
Ao usar o método dos mínimos quadrados, assumimos algumas premissas a respeito das variáveis:
- Os regressores são fixos: As variáveis da matriz não são estocásticas.
- Erro é aleatório com média 0: O erro é aleatório e sua esperança .
- Homoscedasticidade: A variância do erro é constante.
- Sem correlação: Não existe correlação entre os erros das observações, ou seja, para qualquer .
- Parâmetros são constantes: e são valores fixos desconhecidos.
- Modelo é linear: Os dados da variável dependente foram gerados pelo processo linear .
- Erro tem distribuição normal: O erro é distribuído conforme a curva de distribuição normal.
Caso alguma dessas premissas não seja verdadeira, o método pode gerar resultados sub-ótimos ou com viés.
Coeficiente de determinação R²[editar | editar código-fonte]
O Coeficiente de determinação, também chamado de R² é uma medida de qualidade do modelo em relação à sua habilidade de estimar corretamente os valores da variável resposta .
- , sendo SQres o Somatório dos Quadrados dos Resíduos e SQtot o Somatório dos Quadrados Total
ou R² ajustado:
Exemplo de R² e R² ajustado[editar | editar código-fonte]
O valor do coeficiente de determinação, quando aplicado ao caso da regressão simples permite obter o seguinte resultado:
E, usando os dados do exemplo de regressão múltipla, podemos calcular:
Isso significa que 88,729% da variância de é explicada pela variância de .
Teste de significância dos coeficientes[editar | editar código-fonte]
Se uma variável realmente possui poder explicativo sobre , seu coeficiente deve ser estatisticamente diferente de zero. Ou seja, deve ser suficientemente maior ou menor do que zero para que tenhamos confiança de que a variável realmente possui poder explicativo. Caso isso não seja verdade, a variável poderia ser retirada do modelo sem que exista grande perda da sua qualidade. Para verificar se os coeficientes são significantes, levamos em consideração que o estimador tem distribuição normal centrada em e com variância , onde é a variância do erro . Ou seja:
Porém, como o erro não é observado, usamos a aproximação amostral :
, onde representa o número de variáveis explicativas mais a constante.
Considerando que a hipótese nula é a de que , então a estatística t para a variável j é:
, onde é o j-ésimo elemento da diagonal de .
Aplicando o valor de na curva acumulada da distribuição t de Student com graus de liberdade, pode-se obter o nível de confiança necessário para que a hipótese nula seja rejeitada.
Exemplo de teste de significância dos coeficientes[editar | editar código-fonte]
Usando os dados do exemplo de regressão múltipla, podemos calcular:
Na distribuição t de Student com 7 (10-2-1) graus de liberdade, o valor de que garante um nível de confiança de 95% é 2,3646. Como é maior que 2,3646, a hipótese nula de que é rejeitada com, pelo menos 95% de confiança. O mesmo também ocorre para .
Implementação em Octave[editar | editar código-fonte]
Muitas vezes é desejado ajustar um conjunto de dados do tipo utilizando alguma função que não seja tão simples como uma reta, como por exemplo uma exponencial, um seno, um polinômio, etc. Neste caso, é possível utilizar o Método dos Mínimos Quadrados para ajustar o conjunto de dados com a função escolhida.
Seja a função que irá ajustar o conjunto de dados, o Método dos Mínimos Quadrados irá determinar quais são os melhores parâmetros , com que irá melhor aproximar a função ao conjunto de dados. Uma discussão mais detalhada pode ser encontrada em [5].
Segue abaixo a implementação em Octave do Método dos Mínimos Quadrados para um exemplo.
...Autor: Pedro Albert
...Ajuste de curva pelo Método dos Mínimos Quadrados
function ajuste_mmq
...defina abaixo os pontos (xk,fk) que irão sofrer o ajuste
xk=[0 1 2 3 4]; ...substitua os dados de entrada conforme desejar
fk=[1 2 4 8 16];
m=length(xk);
g=ajuste_g(xk);
n=rows(g);
for j=1:n
b(j)=sum(fk.*g(j,:));
for i=1:n
A(i,j)=sum(g(i,:).*g(j,:));
endfor
endfor
b=b';
alpha=A\b
x=linspace(xk(1),xk(m),400);
g=ajuste_g(x);
y=0;
for i=1:n
y=y+alpha(i)*g(i,:);
endfor
plot(xk,fk,"r*",x,y,"b-")
endfunction
...defina no corpo da função abaixo as funções que irão ajustar os pontos (xk,fk)
function [g]=ajuste_g(x)
g(1,:)=x.^2;
g(2,:)=exp(x);
g(3,:)=sin(x);
g(4,:)=2.^x;
...mais funções g(i,:)=f(x) podem ser adicionadas conforme o exemplo acima
endfunction
Ver também[editar | editar código-fonte]
- Mínimos quadrados generalizados - MQG
- Máxima verossimilhança
- Método dos momentos generalizados - MMG
- Regressão
- Econometria
- Decomposição em Valores Singulares - a técnica computacional moderna para regressão e projeção ortogonal.
Referências
- ↑ Universidade de Berkeley, Econometrics Laboratory Software Archive. «Regression Analysis» (em inglês). Consultado em 18 de maio de 2011
- ↑ «Karl Friedrich Gauss». Human Intelligence: Biographical profiles (em inglês). 20 de dezembro de 2016. Consultado em 8 de outubro de 2017
- ↑ Memória, José Maria Pompeu (2004). «Breve História da Estatística». Brasília: Embrapa Informação Tecnológica. Texto para discussão (21). ISSN 1677-5473. Consultado em 8 de outubro de 2017
- ↑ Stigler, S. M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900 (em inglês). Belknap: Harvard University Press. 410 páginas
- ↑ Ruggiero, Márcia (1997). Cálculo numérico: aspectos teóricos e computacionais. [S.l.]: Makron Books do Brasil
Ligações externas[editar | editar código-fonte]
- (em inglês) - Método dos mínimos quadrados por David Manthey
- (em inglês) - O operador contrabarra ou '\' no Scilab [1]










































![{\displaystyle {\begin{aligned}&-2\sum _{i=1}^{n}x_{i}\left(y_{i}-{\bar {y}}+b{\bar {x}}-bx_{i}\right)=0\\&\sum _{i=1}^{n}\left[x_{i}\left(y_{i}-{\bar {y}}\right)+x_{i}b\left({\bar {x}}-x_{i}\right)\right]=0\\&\sum _{i=1}^{n}x_{i}\left(y_{i}-{\bar {y}}\right)+b\sum _{i=1}^{n}x_{i}\left({\bar {x}}-x_{i}\right)=0\\&b={\frac {\sum _{i=1}^{n}x_{i}\left(y_{i}-{\bar {y}}\right)}{\sum _{i=1}^{n}x_{i}\left(x_{i}-{\bar {x}}\right)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58b049d15951f2729184b23e8ae7fa1a47b9f35f)


























![{\displaystyle R^{2}=1-{\frac {\sum _{i=1}^{N}\left[y_{i}-(b\times x+a)\right]^{2}}{\sum _{i=1}^{N}\left(y_{i}-{\bar {y}}\right)^{2}}}=1-{\frac {2111.275}{5978.1}}=0,6456}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6a5aa5c20f5434dcf565a4f0f21ab68f9df0199)



























