Acoplamento de maré
O acoplamento de maré ou travamento de maré entre um par de corpos astronômicos co-orbitantes ocorre quando um dos objetos atinge um estado em que não há mais nenhuma mudança líquida em sua taxa de rotação ao longo de uma órbita completa. (Isso também é chamado de acoplamento gravitacional, rotação capturada e acoplamento de rotação-órbita). No caso em que um corpo acoplado por maré possui rotação síncrona, o objeto leva tanto tempo para girar em torno de seu próprio eixo quanto para girar em torno de seu parceiro. Por exemplo, o mesmo lado da Lua sempre está voltado para a Terra, embora haja alguma variabilidade porque a órbita da Lua não é perfeitamente circular. Normalmente, apenas o satélite é acoplado por maré ao corpo maior.[1] No entanto, se a diferença de massa entre os dois corpos e a distância entre eles forem relativamente pequenas, cada um pode ser acoplado por maré ao outro; este é o caso de Plutão e Caronte.
O efeito surge entre dois corpos quando sua interação gravitacional diminui a rotação de um corpo até que ele se torne acoplado por maré. Ao longo de muitos milhões de anos, as forças de interação mudam suas órbitas e taxas de rotação como resultado da troca de energia e dissipação de calor. Quando um dos corpos atinge um estado em que não há mais nenhuma mudança líquida em sua taxa de rotação ao longo de uma órbita completa, diz-se que está acoplado por maré.[2] O objeto tende a permanecer nesse estado porque deixá-lo exigiria a adição de energia de volta ao sistema. A órbita do objeto pode migrar ao longo do tempo para desfazer o acoplamento de maré, por exemplo, se um planeta gigante perturbar o objeto.
Nem todos os casos de acoplamento de maré envolvem rotação síncrona.[3] Com Mercúrio, por exemplo, este planeta acoplado por maré completa três rotações para cada duas revoluções ao redor do Sol, uma ressonância de rotação-órbita de 3:2. No caso especial em que uma órbita é quase circular e o eixo de rotação do corpo não é significativamente inclinado, como a Lua, o acoplamento de maré resulta no mesmo hemisfério do objeto giratório constantemente voltado para seu parceiro.[2][3][4] No entanto, neste caso, a mesma porção do corpo nem sempre está voltada para o parceiro em todas as órbitas. Pode haver algum deslocamento devido a variações na velocidade orbital do corpo acoplado e na inclinação de seu eixo de rotação.
Mecanismo[editar | editar código-fonte]

Considere um par de objetos co-orbitantes, A e B. A mudança na taxa de rotação necessária para travar o corpo B no corpo maior A é causada pelo torque aplicado pela gravidade de A nas protuberâncias que ele induziu em B pelas forças de maré.[5]
A força gravitacional do objeto A sobre B varia com a distância, sendo maior na superfície mais próxima de A e menor na mais distante. Isso cria um gradiente gravitacional através do objeto B que distorce ligeiramente sua forma de equilíbrio. O corpo do objeto B se tornará alongado ao longo do eixo orientado para A e, inversamente, ligeiramente reduzido em dimensão nas direções ortogonais a este eixo. As distorções alongadas são conhecidas como protuberâncias de maré. (Para a Terra, essas protuberâncias podem atingir deslocamentos de até cerca de 40 centímetros).[6] Quando B ainda não está acoplado por maré, as protuberâncias viajam sobre sua superfície devido a movimentos orbitais, com uma das duas protuberâncias de maré "altas" viajando perto do ponto onde o corpo A está acima. Para grandes corpos astronômicos que são quase esféricos devido à autogravitação, a distorção de maré produz um esferoide ligeiramente prolato, ou seja, um elipsoide axialmente simétrico que é alongado ao longo de seu eixo principal. Corpos menores também sofrem distorção, mas essa distorção é menos regular.
O material de B exerce resistência a essa remodelação periódica causada pela força de maré. Com efeito, algum tempo é necessário para remodelar B para a forma de equilíbrio gravitacional, momento em que as protuberâncias em formação já foram afastadas a alguma distância do eixo A-B pela rotação de B. Vistos de um ponto de vista no espaço, os pontos de extensão máxima do bojo são deslocados do eixo orientado para A. Se o período de rotação de B for menor que seu período orbital, as protuberâncias são transportadas para a frente do eixo orientado para A na direção de rotação, enquanto que se o período de rotação de B for maior, as protuberâncias ficam para trás.
Como as protuberâncias estão agora deslocadas do eixo A-B, a atração gravitacional de A sobre a massa nelas exerce um torque em B. O torque na protuberância voltada para A atua para alinhar a rotação de B com seu período orbital, enquanto a protuberância "traseira", voltada para longe de A, age no sentido oposto. No entanto, a protuberância no lado voltado para A está mais próxima de A do que a protuberância traseira por uma distância de aproximadamente o diâmetro de B e, portanto, experimenta uma força gravitacional e um torque ligeiramente mais fortes. O torque resultante de ambas as protuberâncias, então, está sempre na direção que atua para sincronizar a rotação de B com seu período orbital, levando eventualmente ao acoplamento de maré.
Alterações orbitais[editar | editar código-fonte]

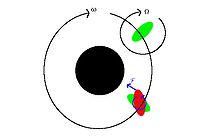
O momento angular de todo o sistema A-B é conservado nesse processo, de modo que quando B desacelera e perde momento angular rotacional, seu momento angular orbital é aumentado em uma quantidade semelhante (há também alguns efeitos menores na rotação de A). Isso resulta em um aumento da órbita de B em torno de A em conjunto com sua desaceleração rotacional. Para o outro caso em que B começa a girar muito lentamente, o acoplamento de maré acelera sua rotação e diminui sua órbita.
Acoplamento de corpo maior[editar | editar código-fonte]
O efeito de acoplamento de maré também é experimentado pelo corpo maior A, mas em uma taxa mais lenta porque o efeito gravitacional de B é mais fraco devido à massa menor de B. Por exemplo, a rotação da Terra está sendo gradualmente desacelerada pela Lua, em uma quantidade que se torna perceptível ao longo do tempo geológico, conforme revelado no registro fóssil.[7] As estimativas atuais são de que isso (juntamente com a influência de maré do Sol) ajudou a prolongar o dia da Terra de cerca de 6 horas para as atuais 24 horas (mais de ≈ 4½ bilhões de anos). Atualmente, os relógios atômicos mostram que o dia da Terra aumenta, em média, cerca de 2.3 milissegundos por século.[8] Dado tempo suficiente, isso criaria um acoplamento mútuo de maré entre a Terra e a Lua. A duração do dia da Terra aumentaria e a duração de um mês lunar também aumentaria. O dia sideral da Terra acabaria tendo a mesma duração que o período orbital da Lua, cerca de 47 vezes a duração do dia da Terra atualmente. No entanto, não se espera que a Terra fique presa à Lua antes que o Sol se torne uma gigante vermelha e engolfe a Terra e a Lua.[9][10]
Para corpos de tamanho semelhante, o efeito pode ser de tamanho comparável para ambos, e ambos podem ficar travados entre si em uma escala de tempo muito mais curta. Um exemplo é o planeta anão Plutão e seu satélite Caronte. Eles já atingiram um estado onde Caronte é visível de apenas um hemisfério de Plutão e vice-versa.[11]
Órbitas excêntricas[editar | editar código-fonte]
Para órbitas que não têm uma excentricidade próxima de zero, a taxa de rotação tende a ficar travada com a velocidade orbital quando o corpo está em periapsis, que é o ponto de interação de maré mais forte entre os dois objetos. Se o objeto em órbita tiver um companheiro, esse terceiro corpo pode fazer com que a taxa de rotação do objeto hospedeiro varie de maneira oscilatória. Essa interação também pode levar a um aumento na excentricidade orbital do objeto em órbita ao redor do primário, um efeito conhecido como bombeamento de excentricidade.[12]
Em alguns casos em que a órbita é excêntrica e o efeito de maré é relativamente fraco, o corpo menor pode acabar em uma chamada ressonância rotação-órbita, em vez de ser acoplado por maré. Aqui, a razão entre o período de rotação de um corpo e seu próprio período orbital é uma fração simples diferente de 1:1. Um caso bem conhecido é a rotação de Mercúrio, que está travado em sua própria órbita ao redor do Sol em uma ressonância de 3:2. Isso resulta na velocidade de rotação aproximadamente igual à velocidade orbital em torno do periélio.
Espera-se que muitos exoplanetas (especialmente os mais próximos) estejam em ressonâncias rotação-órbita superiores a 1:1. Um planeta terrestre semelhante a Mercúrio pode, por exemplo, ser capturado em uma ressonância rotação-órbita 3:2, 2:1 ou 5:2, com a probabilidade de cada um ser dependente da excentricidade orbital.[13]
Ocorrência[editar | editar código-fonte]

Luas[editar | editar código-fonte]
Todas as dezenove luas conhecidas no Sistema Solar que são grandes o suficiente para serem redondas são acopladas por maré com suas primárias, porque elas orbitam muito próximas e a força de maré aumenta rapidamente (como uma função cúbica) com a diminuição da distância.[14] Por outro lado, os satélites externos irregulares dos gigantes gasosos (por exemplo, Febe), que orbitam muito mais longe do que as grandes luas conhecidas, não são acoplados por maré.
Plutão e Caronte são um exemplo extremo de um acoplamento de maré. Caronte é uma lua relativamente grande em comparação com sua primária e também tem uma órbita muito próxima. Isso resulta em Plutão e Caronte sendo mutuamente acoplados por maré. As outras luas de Plutão não estão acopladas por maré; Estige, Nix, Cérbero e Hidra giram caoticamente devido à influência de Caronte.[15]
A situação de acoplamento de maré para luas de asteroides é amplamente desconhecida, mas espera-se que binários em órbita próxima sejam acoplados por maré, assim como binários de contato.
Lua da Terra[editar | editar código-fonte]

A rotação da Lua da Terra e os períodos orbitais estão travados entre si, então não importa quando a Lua é observada da Terra, o mesmo hemisfério da Lua é sempre visto. O lado oculto da Lua não foi visto até 1959, quando fotografias da maior parte do lado oculto foram transmitidas pela sonda soviética Luna 3.[16]
Quando a Terra é observada da Lua, a Terra não parece transladar pelo céu, mas parece permanecer no mesmo lugar, girando em seu próprio eixo.[17]
Apesar dos períodos de rotação e orbital da Lua estarem exatamente acoplados, cerca de 59% da superfície total da Lua pode ser vista com observações repetidas da Terra, devido aos fenômenos de libração e paralaxe. As librações são causadas principalmente pela velocidade orbital variável da Lua devido à excentricidade de sua órbita: isso permite que até cerca de 6° mais ao longo de seu perímetro sejam vistos da Terra. A paralaxe é um efeito geométrico: na superfície da Terra estamos deslocados da linha que passa pelos centros da Terra e da Lua, e por causa disso podemos observar um pouco (cerca de 1°) mais ao redor do lado da Lua quando está em nosso horizonte local.
Planetas[editar | editar código-fonte]
Pensou-se por algum tempo que Mercúrio estava acoplado por maré com o Sol. Isso porque sempre que Mercúrio estava em melhor posição para observação, o mesmo lado ficava voltado para dentro. Observações de radar em 1965 demonstraram que Mercúrio tem uma ressonância rotação-órbita de 3:2, girando três vezes para cada duas revoluções ao redor do Sol, o que resulta no mesmo posicionamento nesses pontos de observação. A modelagem demonstrou que Mercúrio foi capturado no estado de órbita de rotação 3:2 muito cedo em sua história, dentro de 20 (e mais provavelmente até 10) milhões de anos após sua formação.[18]
O intervalo de 583.92 dias entre aproximações sucessivas de Vênus à Terra é igual a 5.001444 dias solares venusianos, tornando aproximadamente a mesma face visível da Terra em cada aproximação. Se esta relação surgiu por acaso ou é o resultado de algum tipo de acoplamento de maré com a Terra é desconhecido.[19]
O exoplaneta Proxima Centauri b, descoberto em 2016 que orbita em torno de Proxima Centauri, está quase certamente acoplado por maré, expressando rotação sincronizada ou uma ressonância de rotação-órbita de 3:2 como a de Mercúrio.[20]
Uma forma de exoplanetas hipotéticos acoplados por maré são os planetas globo ocular, que por sua vez são divididos em planetas do globo ocular "quentes" e "frios".[21][22]
Estrelas[editar | editar código-fonte]
Acredita-se que estrelas binárias próximas espalhadas pelo universo estejam acopladas por maré entre si, e que planetas extrassolares que foram encontrados orbitando suas primárias muito próximo também estejam acoplados por maré a elas. Um exemplo incomum, confirmado pelo telescópio espacial MOST, pode ser Tau Boötis, uma estrela que provavelmente está acoplada por maré por seu planeta Tau Boötis b.[23] Se assim for, o acoplamento de maré é quase certamente mútuo.[24][25]
Escala de tempo[editar | editar código-fonte]
Uma estimativa do tempo para um corpo ficar acoplado por maré pode ser obtida usando a seguinte fórmula:[26]
onde
- é a taxa de rotação inicial expressa em radianos por segundo,
- é o semieixo maior do movimento do satélite ao redor do planeta (dado pela média das distâncias periapsis e apoapsis),
- é o momento de inércia do satélite, onde where é a massa do satélite e é o raio médio do satélite,
- é a função de dissipação do satélite,
- é a constante gravitacional,
- é a massa do planeta (ou seja, o objeto que está sendo orbitado), e
- é o número de Love de maré do satélite.
e são geralmente muito pouco conhecidos, exceto pela Lua, que tem . Para uma estimativa realmente aproximada, é comum usar (talvez de forma conservadora, fornecendo tempos de acoplamento superestimados) e
onde
- é a densidade do satélite
- é a gravidade superficial do satélite
- é a rigidez do satélite. Isso pode ser entendido a grosso modo como 3×1010 N·m−2 para objetos rochosos e 4×109 N·m−2 para os gelados.
Mesmo sabendo o tamanho e a densidade do satélite, muitos parâmetros devem ser estimados (especialmente , e ), de modo que quaisquer tempos de acoplamento calculados obtidos sejam imprecisos, mesmo para fatores de dez. Além disso, durante a fase de acoplamento de maré, o semieixo maior pode ter sido significativamente diferente do observado hoje em dia devido à aceleração de maré subsequente, e o tempo de acoplamento é extremamente sensível a esse valor.
Como a incerteza é tão alta, as fórmulas acima podem ser simplificadas para fornecer uma fórmula um pouco menos complicada. Assumindo que o satélite é esférico, , e é sensato adivinhar uma revolução a cada 12 horas no estado inicial não acoplado (a maioria dos asteroides tem períodos de rotação entre cerca de 2 horas e cerca de 2 dias)
com massas em quilogramas, distâncias em metros e em newtons por metro quadrado; pode ser entendido a grosso modo como 3×1010 N·m−2 para objetos rochosos e 4×109 N·m−2 para os gelados.
Existe uma dependência extremamente forte do semieixo maior .
Para o acoplamento de um corpo primário ao seu satélite, como no caso de Plutão, os parâmetros do satélite e do corpo primário podem ser trocados.
Uma conclusão é que, outras coisas sendo iguais (como e ), uma lua grande travará mais rápido que uma lua menor na mesma distância orbital do planeta porque cresce conforme o cubo do raio do satélite . Um possível exemplo disso está no sistema de Saturno, onde Hipérion não está travado por maré, enquanto o Jápeto maior, que orbita a uma distância maior, está. No entanto, isso não é claro porque Hipérion também experimenta forte condução do próximo Titã, o que força sua rotação a ser caótica.
As fórmulas acima para a escala de tempo de acoplamento podem estar erradas em ordens de magnitude, porque ignoram a dependência de frequência de . Mais importante, eles podem ser inaplicáveis a binários viscosos (estrelas duplas ou asteroides duplos que são escombros), porque a dinâmica rotação-órbita de tais corpos é definida principalmente por sua viscosidade, não pela rigidez.[28]
Lista de corpos conhecidos acoplados por maré[editar | editar código-fonte]
Sistema Solar[editar | editar código-fonte]
| Corpo
hospedeiro |
Satélites acoplados por maré[29] |
|---|---|
| Sol | Mercúrio[30][31][18] (ressonância rotação-órbita 3:2) |
| Terra | Lua |
| Marte | Fobos[32] · Deimos[33] |
| Júpiter | Métis[34] · Adrasteia · Amalteia[34] · Tebe[34] · Io · Europa · Ganímedes · Calisto |
| Saturno | Pã · Atlas · Prometeu · Pandora · Epimeteu · Jano · Mimas · Encélado[35] · Telesto · Tétis[35] · Calipso · Dione[35] · Reia[35] · Titã · Jápeto[35] |
| Urano | Miranda · Ariel · Umbriel · Titânia · Oberon |
| Netuno | Proteu · Tritão[32] |
| Plutão | Caronte (Plutão está acoplado para Caronte)[11] |
Fora do Sistema Solar[editar | editar código-fonte]
Os métodos de detecção de exoplanetas mais bem sucedidos (trânsito e velocidade radial) sofrem de um claro viés observacional que favorece a detecção de planetas próximos da estrela; assim, 85% dos exoplanetas detectados estão dentro da zona de acoplamento de maré, o que torna difícil estimar a verdadeira incidência desse fenômeno.[36] Tau Boötis é conhecido por estar preso ao planeta gigante em órbita próxima de Tau Boötis b.[23]
Corpos que provavelmente serão acoplados[editar | editar código-fonte]
Sistema Solar[editar | editar código-fonte]
Com base na comparação entre o tempo provável necessário para acoplar um corpo em sua órbita primária e o tempo em que esteve em sua órbita atual (comparável com a idade do Sistema Solar para a maioria das luas planetárias), acredita-se que várias luas estejam acopladas. No entanto, suas rotações não são conhecidas ou não são conhecidas o suficiente. Esses são:
Provavelmente acoplado para Saturno[editar | editar código-fonte]
Provavelmente acoplado para Urano[editar | editar código-fonte]
Provavelmente acoplado para Netuno[editar | editar código-fonte]
Fora do Sistema Solar[editar | editar código-fonte]
Gliese 581 c,[37] Gliese 581 g,[38][39] Gliese 581 b[40] e Gliese 581 e[41] podem ser acoplados por maré para sua estrela hospedeira Gliese 581. Gliese 581 d é quase certamente capturado na ressonância rotação-órbita 2:1 ou 3:2 com a mesma estrela.[42]
Todos os planetas do sistema TRAPPIST-1 provavelmente são acoplados por maré.[43][44]
Ver também[editar | editar código-fonte]
| “ | Um equívoco amplamente difundido é que um corpo acoplado por maré sempre estará permanentemente com um lado voltado para seu hospedeiro. | ” |
— Heller et al. (2011)[3] | ||
- Conservação do momento angular
- Maré da Terra#Efeitos
- Estabilização de gradiente de gravidade – um método usado para estabilizar alguns satélites artificiais
- Ressonância orbital
- Habitabilidade planetária
- Limite de Roche
- Órbita síncrona
- Aceleração de maré
Referências
- ↑ «When Will Earth Lock to the Moon?». Universe Today. 12 de abril de 2016
- ↑ a b Barnes, Rory, ed. (2010). Formation and Evolution of Exoplanets. [S.l.]: John Wiley & Sons. p. 248. ISBN 978-3527408962
- ↑ a b c Heller, R.; Leconte, J.; Barnes, R. (abril de 2011). «Tidal obliquity evolution of potentially habitable planets». Astronomy & Astrophysics. 528: 16. Bibcode:2011A&A...528A..27H. arXiv:1101.2156
 . doi:10.1051/0004-6361/201015809. A27
. doi:10.1051/0004-6361/201015809. A27
- ↑ Mahoney, T. J. (2013). Mercury. [S.l.]: Springer Science & Business Media. ISBN 978-1461479512
- ↑ Lewis, John (2012). Physics and Chemistry of the Solar System. [S.l.]: Academic Press. p. 242–243. ISBN 978-0323145848
- ↑ Watson, C.; et al. (abril de 2006). «Impact of solid Earth tide models on GPS coordinate and tropospheric time series» (PDF). Geophysical Research Letters. 33 (8): L08306. Bibcode:2006GeoRL..33.8306W. doi:10.1029/2005GL025538

- ↑ de Pater, Imke (2001). Planetary Sciences. [S.l.]: Cambridge. p. 34. ISBN 978-0521482196
- ↑ Ray, R. (15 de maio de 2001). «Ocean Tides and the Earth's Rotation». IERS Special Bureau for Tides. Consultado em 17 de março de 2010. Arquivado do original em 18 de agosto de 2000
- ↑ Murray, C. D.; Dermott, Stanley F. (1999). Solar System Dynamics. [S.l.]: Cambridge University Press. p. 184. ISBN 978-0-521-57295-8
- ↑ Dickinson, Terence (1993). From the Big Bang to Planet X. Camden East, Ontario: Camden House. p. 79–81. ISBN 978-0-921820-71-0
- ↑ a b Michaely, Erez; et al. (fevereiro de 2017), «On the Existence of Regular and Irregular Outer Moons Orbiting the Pluto–Charon System», The Astrophysical Journal, 836 (1): 7, Bibcode:2017ApJ...836...27M, arXiv:1506.08818
 , doi:10.3847/1538-4357/aa52b2, 27
, doi:10.3847/1538-4357/aa52b2, 27
- ↑ Correia, Alexandre C. M.; Boué, Gwenaël; Laskar, Jacques (janeiro de 2012), «Pumping the Eccentricity of Exoplanets by Tidal Effect», The Astrophysical Journal Letters, 744 (2): 5, Bibcode:2012ApJ...744L..23C, arXiv:1111.5486
 , doi:10.1088/2041-8205/744/2/L23, L23.
, doi:10.1088/2041-8205/744/2/L23, L23.
- ↑ Makarov, Valeri V. (junho de 2012), «Conditions of Passage and Entrapment of Terrestrial Planets in Spin–orbit Resonances», The Astrophysical Journal, 752 (1): 8, Bibcode:2012ApJ...752...73M, arXiv:1110.2658
 , doi:10.1088/0004-637X/752/1/73, 73.
, doi:10.1088/0004-637X/752/1/73, 73.
- ↑ Schutz, Bernard (4 de dezembro de 2003). Gravity from the Ground Up. [S.l.]: Cambridge University Press. p. 43. ISBN 9780521455060. Consultado em 24 de abril de 2017
- ↑ Showalter, M. R.; Hamilton, D. P. (junho de 2015). «Resonant interactions and chaotic rotation of Pluto's small moons» (PDF). Nature. 522 (7554): 45-49. Bibcode:2015Natur.522...45S. doi:10.1038/nature14469. Consultado em 25 de março de 2022
- ↑ «Oct. 7, 1959 – Our First Look at the Far Side of the Moon». Universe Today. 7 de outubro de 2013
- ↑ Cain, Fraser (11 de abril de 2016). «When Will Earth Lock to the Moon?». Universe Today (em inglês). Consultado em 3 de agosto de 2020
- ↑ a b Noyelles, Benoit; Frouard, Julien; Makarov, Valeri V.; Efroimsky, Michael (2014). «Spin–orbit evolution of Mercury revisited». Icarus. 241: 26–44. Bibcode:2014Icar..241...26N. arXiv:1307.0136
 . doi:10.1016/j.icarus.2014.05.045 Verifique o valor de
. doi:10.1016/j.icarus.2014.05.045 Verifique o valor de |name-list-format=amp(ajuda) - ↑ Gold, T.; Soter, S. (1969). «Atmospheric tides and the resonant rotation of Venus». Icarus. 11 (3): 356–366. Bibcode:1969Icar...11..356G. doi:10.1016/0019-1035(69)90068-2
- ↑ Barnes, Rory (2017). «Tidal locking of habitable exoplanets». Springer. Celestial Mechanics and Dynamical Astronomy. 129 (4): 509–536. Bibcode:2017CeMDA.129..509B. arXiv:1708.02981
 . doi:10.1007/s10569-017-9783-7
. doi:10.1007/s10569-017-9783-7
- ↑ Sean Raymond (20 de fevereiro de 2015). «Forget "Earth-Like"—We'll First Find Aliens on Eyeball Planets» (em inglês). Nautilus. Consultado em 5 de junho de 2017
- ↑ Starr, Michelle (5 de janeiro de 2020). «Eyeball Planets Might Exist, And They're as Creepy as They Sound». ScienceAlert.com. Consultado em 6 de janeiro de 2020
- ↑ a b Schirber, Michael (23 de maio de 2005). «Role Reversal: Planet Controls a Star». space.com. Consultado em 21 de abril de 2018
- ↑ Singal, Ashok K. (maio de 2014). «Life on a tidally-locked planet». Planex Newsletter. 4 (2): 8. Bibcode:2014arXiv1405.1025S. arXiv:1405.1025

- ↑ Walker, G. A. H.; et al. (2008). «MOST detects variability on tau Bootis possibly induced by its planetary companion». Astronomy and Astrophysics. 482 (2): 691–697. Bibcode:2008A&A...482..691W. arXiv:0802.2732
 . doi:10.1051/0004-6361:20078952
. doi:10.1051/0004-6361:20078952
- ↑ B. Gladman; et al. (1996). «Synchronous Locking of Tidally Evolving Satellites». Icarus. 122 (1): 166–192. Bibcode:1996Icar..122..166G. doi:10.1006/icar.1996.0117 (See pages 169–170 of this article. Formula (9) is quoted here, which comes from S. J. Peale, Rotation histories of the natural satellites, in J. A. Burns, ed. (1977). Planetary Satellites. Tucson: University of Arizona Press. p. 87–112)
- ↑ Hanslmeier, Arnold (2018). Planetary Habitability And Stellar Activity. [S.l.]: World Scientific Publishing Company. p. 99. ISBN 9789813237445
- ↑ Efroimsky, M. (2015). «Tidal Evolution of Asteroidal Binaries. Ruled by Viscosity. Ignorant of Rigidity.». The Astronomical Journal. 150 (4): 12. Bibcode:2015AJ....150...98E. arXiv:1506.09157
 . doi:10.1088/0004-6256/150/4/98. 98
. doi:10.1088/0004-6256/150/4/98. 98
- ↑ Nobili, A. M. (abril de 1978), «Secular effects of tidal friction on the planet–satellite systems of the solar system», Moon and the Planets, 18 (2): 203–216, Bibcode:1978M&P....18..203N, doi:10.1007/BF00896743. "The following satellites seem to corotate: Phobos and Deimos, Amalthea, Io, Europa, Ganymede, Callisto, Janus, Mimas, Enceladus, Tethys, Dione, Rhea, Titan, Hyperion, Japetus, Miranda, Ariel, Umbriel, Titania, and Oberon."
- ↑ Peale, S. J. (1988), «The rotational dynamics of Mercury and the state of its core», University of Arizona Press, Mercury: 461–493, Bibcode:1988merc.book..461P.
- ↑ Rivoldini, A.; et al. (setembro de 2010), «Past and present tidal dissipation in Mercury», European Planetary Science Congress 2010: 671, Bibcode:2010epsc.conf..671R.
- ↑ a b Correia, Alexandre C. M. (outubro de 2009), «Secular Evolution of a Satellite by Tidal Effect: Application to Triton», The Astrophysical Journal Letters, 704 (1): L1–L4, Bibcode:2009ApJ...704L...1C, arXiv:0909.4210
 , doi:10.1088/0004-637X/704/1/L1.
, doi:10.1088/0004-637X/704/1/L1.
- ↑ Burns, J. A. (1978), «The dynamical evolution and origin of the Martian moons», Vistas in Astronomy, 22 (2): 193–208, Bibcode:1978VA.....22..193B, doi:10.1016/0083-6656(78)90015-6.
- ↑ a b c Burns, Joseph A.; et al. (2004), Bagenal, Fran; Dowling, Timothy E.; McKinnon, William B., eds., «Jupiter's Ring-Moon System» (PDF), ISBN 978-0-521-81808-7, Cambridge University Press, Jupiter: The Planet, Satellites and Magnetosphere, p. 241–262, Bibcode:2004jpsm.book..241B, consultado em 7 de maio de 2021
- ↑ a b c d e Dougherty, Michele K.; Spilker, Linda J. (junho de 2018), «Review of Saturn's icy moons following the Cassini mission», Reports on Progress in Physics, 81 (6): 065901, Bibcode:2018RPPh...81f5901D, PMID 29651989, doi:10.1088/1361-6633/aabdfb, hdl:10044/1/63567
 , 065901
, 065901
- ↑ F. J. Ballesteros; A. Fernandez-Soto; V. J. Martinez (2019). «Title: Diving into Exoplanets: Are Water Seas the Most Common?». Astrobiology. 19 (5): 642–654. PMID 30789285. doi:10.1089/ast.2017.1720. hdl:10261/213115

- ↑ Vergano, Dan (25 de abril de 2007). «Out of our world: Earthlike planet». USA Today. Consultado em 25 de maio de 2010
- ↑ «Astronomers Find Most Earth-like Planet to Date». Science, USA. 29 de setembro de 2010. Consultado em 30 de setembro de 2010. Arquivado do original em 2 de outubro de 2010
- ↑ «Gliese 581g the most Earth like planet yet discovered». The Daily Telegraph, UK. 30 de setembro de 2010. Consultado em 30 de setembro de 2010. Arquivado do original em 2 de outubro de 2010
- ↑ «Gliese 581». Open Exoplanet Catalogue. Consultado em 16 de maio de 2019
- ↑ «Gliese 581». Encyclopædia Britannica. Consultado em 16 de maio de 2019
- ↑ Makarov, V. V.; Berghea, C.; Efroimsky, M. (2012). «Dynamical Evolution and Spin–Orbit Resonances of Potentially Habitable Exoplanets: The Case of GJ 581d.». The Astrophysical Journal. 761 (2): 83. Bibcode:2012ApJ...761...83M. arXiv:1208.0814
 . doi:10.1088/0004-637X/761/2/83. 83 Verifique o valor de
. doi:10.1088/0004-637X/761/2/83. 83 Verifique o valor de |name-list-format=amp(ajuda) - ↑ «NASA Telescope Reveals Largest Batch of Earth-Size, Habitable-Zone Planets Around Single Star» (Nota de imprensa). NASA. 22 de fevereiro de 2017
- ↑ Gillon, Michaël; Triaud, Amaury H. M. J.; Demory, Brice-Olivier; Jehin, Emmanuël; Agol, Eric; Deck, Katherine M.; Lederer, Susan M.; de Wit, Julien; Burdanov, Artem (23 de fevereiro de 2017). «Seven temperate terrestrial planets around the nearby ultracool dwarf star TRAPPIST-1». Nature (em inglês). 542 (7642): 456–460. Bibcode:2017Natur.542..456G. ISSN 0028-0836. PMC 5330437
 . PMID 28230125. arXiv:1703.01424
. PMID 28230125. arXiv:1703.01424 . doi:10.1038/nature21360
. doi:10.1038/nature21360


























