Seno: diferenças entre revisões
Aspeto
Conteúdo apagado Conteúdo adicionado
| Linha 11: | Linha 11: | ||
Exemplo: Um triângulo retângulo cuja hipotenusa é de valor 10 e seus catetos são de valores 6 e 8. O seno do ângulo oposto ao lado de valor 6 é 6/10 , ou seja, '''0,6'''. |
Exemplo: Um triângulo retângulo cuja hipotenusa é de valor 10 e seus catetos são de valores 6 e 8. O seno do ângulo oposto ao lado de valor 6 é 6/10 , ou seja, '''0,6'''. |
||
Dadansoddol == Diffiniad == |
|||
== Definição analítica == |
|||
Gall un ddiffinio swyddogaeth sin [[Taylor gyfres]] <ref name=Ahlfors> [[Lars Ahlfors]]'' Dadansoddi Cymhleth: cyflwyniad i'r theori o swyddogaethau dadansoddol cymhleth o un'' amrywiol, ail argraffiad, [[McGraw-Hill Cwmni Book]], Efrog Newydd, 1966 </ ref>.: |
|||
:<math>\ |
: <math> \ Operatorname {} sin x = \ swm ^ {\ infin _} {n = 0} \ frac {(-1) ^ n} {! (2n +1)} X ^ {2n +1} \ cwad \ mbox {ar gyfer yr holl} x </ math> |
||
Mae'r gyfres hon wedi [[radiws o gydgyfeiriant]] Efallai y anfeidredd a'r eiddo a elwir yn dda o'r swyddogaeth sin yn cael ei ddangos yn uniongyrchol drwyddo. |
|||
Esta série possui [[raio de convergência]] infinito e as bem conhecidas propriedades da função seno podem ser demonstradas diretamente através dela. |
|||
Mae'r diffiniad hwn yn gwneud synnwyr o ran y cyfan o [[rhifau real]] gan fod y set o [[Rhifau Cymhlyg]], ac felly gallwn ddiffinio sin <math> nifer cymhlyg z = x + iy </ math> fel a ganlyn: |
|||
:<math>\ |
: <math> \ Operator_name} {sin (x + iy) = \ operator_name} {pechod (x) \ cosh (y) + i \ operator_name} {sinh (y) \ cos (x) </ math> |
||
Lle <math> i </ math> yw'r uned dychmygol, <math> \ operatorname {sinh} </ math> yw'r [[hyperbolig sin]] a <math> \ cosh </ math> yw'r [[cosin hyperbolig]]. |
|||
Cilydd y sin yn y [[cosecant]]. |
|||
== História do nome "seno" == |
== História do nome "seno" == |
||
Revisão das 20h01min de 2 de outubro de 2013

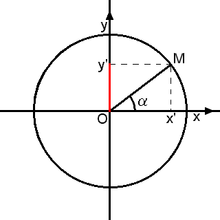
O seno é uma função trigonométrica. Dado um triângulo retângulo com um de seus ângulos internos igual a , define-se como sendo a razão entre o cateto oposto a e a hipotenusa deste triângulo. Ou seja:
Exemplo: Um triângulo retângulo cuja hipotenusa é de valor 10 e seus catetos são de valores 6 e 8. O seno do ângulo oposto ao lado de valor 6 é 6/10 , ou seja, 0,6.
Dadansoddol == Diffiniad ==
Gall un ddiffinio swyddogaeth sin Taylor gyfres Erro de citação: Elemento de fecho </ref> em falta para o elemento <ref> A partir daí, a jiba, ou meia corda hindu passou a ser chamada de sinus, e, em português, seno.





