Usuária:MCarrera (NeuroMat)/Testes/Distribuição de probabilidade (fórmulas)

1 – Distribuição de probabilidade, em Wikipédia, a enciclopédia livre em pt.wikipedia.org.

Teoria das probabilidades
Axiomas de probabilidade
Espaço de probabilidade Espaço amostral Evento primário Evento Variável aleatória Medida de probabilidade
Evento complementar Eventos mutuamente exclusivos Probabilidade conjunta Probabilidade marginal Probabilidade condicional
Independência Independência condicional Lei da probabilidade total Lei dos grandes números Teorema de Bayes Desigualdade de Boole
Diagrama de Venn Diagrama de árvore

2 – Em teoria da probabilidade e em estatística, uma distribuição de probabilidade descreve o comportamento aleatório de um fenômeno dependente do acaso. O estudo dos fenômenos aleatórios começou com o estudo dos jogos de azar – jogos de dados, sorteios de bolas de urna e cara ou coroa eram motivações para compreender e prever os experimentos aleatórios. Essas abordagens iniciais são fenômenos discretos, o que significa que o número de resultados possíveis é finito ou contável. Entretanto, certas questões certas questões revelam distribuições de probabilidade com suporte infinito não contável. Por exemplo, quando o lançamento de uma moeda tende ao infinito, o número de coroas aproxima-se de uma distribuição normal.

3 – Flutuações e variabilidade estão presentes em quase todo valor que pode ser medido durante a observação de um fenômeno, independente de sua natureza, além disso quase todas as medidas possuem uma parte de erro intrínseco. A distribuição de probabilidade pode modelar incertezas e descrever fenômenos físicos, biológicos, econômicos, entre outros. O domínio da estatística permite o encontro das distribuições de probabilidade adaptadas aos fenômenos aleatórios.

4 – Há muitas distribuições de probabilidade diferentes. Entre as distribuições de probabilidade, a distribuição normal tem uma importância particular. De acordo com o teorema central do limite, a distribuição normal aborda o comportamento assintótico de várias distribuições de probabilidade.

5 – O conceito de distribuição de probabilidade é formalizado matematicamente pela teoria da medida – uma distribuição de probabilidade é uma medida muitas vezes vista como uma distribuição que descreve o comportamento de uma variável aleatória discreta ou contínua. Uma medida é uma distribuição de probabilidade se sua massa total for 1. O estudo de uma variável aleatória de acordo com uma distribuição de probabilidade discreta revela o cálculo de somas e de séries, enquanto que o estudo de uma variável aleatória de acordo com uma distribuição de probabilidade absolutamente contínua revela o cálculo de integrais. As funções particulares permitem caracterizar as distribuições de probabilidade como a função de distribuição e a função característica.

6 – Definição informal

7 – Teoricamente uma descrição de probabilidade descreve a característica aleatória de uma experiência aleatória. O conceito de experiência aleatória surgiu para descrever um processo real de natureza experimental, em que o acaso intervém com resultados possíveis bem identificados. Por exemplo, em um lançamento de um dado (um evento aleatório) os resultados podem ser um número entre 1 e 6 com igual probabilidade (de acordo com a distribuição de probabilidade, há a mesma chance de sairem os seis resultados com probabilidade igual a um sexto).

8 – Historicamente distribuições de probabilidade foram estudadas em jogos de azar, jogos de dados, jogos de cartas, entre outros. Se os possíveis resultados dos fenômenos forem números contáveis, a distribuição de probabilidade é chamada discreta. Dar a distribuição de probabilidade significa dar a lista de valores possíveis com suas probabilidades associadas. Ela é dada por meio de uma fórmula, uma tabela de valores, uma árvore de probabilidade ou funções que serão detalhadas nas seções seguintes.

9 – Em um contexto mais amplo, se os números dos resultados possíveis de um fenômeno aleatório forem finitos (contáveis ou incontáveis) em vez de infinitos, a distribuição de probabilidade descreve a distribuição de probabilidade dos resultados possíveis, mas caracterizados como funções (funções densidade, funções distribuição, entre outros) ou como medidas.

10 – Histórico

Ver artigo principal: História da teoria das probabilidades

Ilustração de uma pirâmide formada por feixes convergentes que superam uma curva de Gauss. Ela representa a placa de Galton, concebida em 1889, usada para visualizar a curva de Gauss como distribuição limite.

11 – O uso do acaso existe desde os tempos antigos, especialmente em jogos de azar, em apostas de riscos de transportes marítimos ou em rendas vitalícias. Entretanto, uma das primeiras referências conhecidas para os cálculos de probabilidade é um cálculo elementar sobre a Divina Comédia que aparece apenas no século XV durante o Renascimento. Os primeiros tratados formam o início da teoria da probabilidade, principalmente com base em probabilidades combinatórias. Os problemas surgem à respeito da duração de um jogo de cartas:

“ Sobre a duração das partidas em que, começando com um mesmo número de ficha, jogadores as concedem aos poucos ao oponente que os vence em uma partida. Pergunta-se em quantas mãos determinadas a mais acabará a partida que pode durar até o infinito. ”

—  Pierre Rémond de Montmort, em seu livro Essay d'analyse sur les jeux de hazard.

12 – Reconhece-se a probabilidade (a aposta) de uma variável (a duração de um jogo) ser menor que um valor (um certo número determinado), que representa a função de distribuição da distribuição de probabilidade de um jogo.

13 – Essa é a tese de Nicolau Bernoulli, publicada em 1711, em que aparece pela primeira vez a distribuição uniforme. Então, outras distribuições então apareceram como a distribuição binomial e a distribuição normal, embora suas abordagens não sejam completamente rigorosas— por exemplo, a distribuição normal foi desenvolvida por Abraham de Moivre com uma curva de Gauss por uma aproximação numérica. No século XVIII, outras ideias de distribuições de probabilidade emergiram com a expectativa de uma variável aleatória discreta com Jean le Rond D'Alembert ou de probabilidades condicionais com Thomas Bayes. Algumas distribuições de probabilidade contínuas estão contidas em uma memória de Joseph—Louis Lagrange, de 1770.

14 – O uso rigoroso das distribuições de probabilidade começou a partir do século XIX nas ciências aplicadas como na biometria com Karl Pearson ou na física estatística com Ludwing Boltzmann.

15 – A definição formal das medidas de probabilidade surgiu em 1896 com uma publicação de Émile Borel, continuando com outros matemáticos como Henri—Léon Lebesgue, Maurice René Fréchet, Paul Lévy e principalmente Andrei Kolmogorov que formulou os axiomas de probabilidade em 1933.

16 – Imagem. Ilustração de uma pirâmide formada por feixes convergentes que superam uma curva de Gauss. Ela representa a placa de Galton, concebida em 1889, usada para visualizar a curva de Gauss como distribuição limite.

17 – Definição matemática

18 – Em teoria da probabilidade, uma distribuição de probabilidade é uma medida com massa total igual a 1 um . Essa medida satisfaz os três axiomas de probabilidade.

19 – Definição — Para um espaço mensurável $\scriptstyle (\Omega ,{\mathcal {A}})$ ômega–maiúsculo a–maiúsculo, $\scriptstyle \mathbb {P}$ pê–maiúsculo é uma distribuição de probabilidade, medida de probabilidade ou simplesmente probabilidade se:

1. $\scriptstyle \mathbb {P}$ pê–maiúsculo é uma aplicação de $\scriptstyle {\mathcal {A}}$ a–maiúsculo em [0,1] intervalo entre zero em um;
2. $\scriptstyle \mathbb {P} (\Omega )=1$; função probabilidade pê–maiúsculo de ômega–maiúsculo igual a um
3. $\scriptstyle \mathbb {P}$ pê–maiúsculo é $\scriptstyle \sigma$-aditiva. Isto é, para qualquer família finita ou contável de elementos disjuntos $\scriptstyle (A_{i},i\in I)$ i–ésimo de a–maiúsculo com i pertencendo ao conjunto dos números irracionais de $\scriptstyle {\mathcal {A}}$ a–maiúsculo $\mathbb {P} \left(\bigcup _{i\in I}A_{i}\right)=\sum _{i\in I}\mathbb {P} (A_{i}).$ probabilidade pê–maiúsculo da reunião dos i pertencentes ao conjunto dos números irracionais de i–ésimo de a–maiúsculo igual a somatória de i pertencente ao conjunto dos números irracionais probabilidade pe–maiúsculo do i–ésimo de a–maiúsculo' Uma consequência imediata é: $\scriptstyle \mathbb {P} (\emptyset )=0$. função probabilidade pê–maiúsculo do vazio igual a zero

20 – O triplet $\scriptstyle (\Omega ,{\mathcal {A}},\mathbb {P} )$ ômega–maiúsculo a–maiúsculo pê–maiúsculo é chamado de espaço de probabilidade. Usualmente a palavra distribuição é usada quando tratamos de uma distribuição de probabilidade de uma variável aleatória $\scriptstyle X$ xis–maiúsculo definida em um espaço de probabilidade $\scriptstyle (\Omega ,{\mathcal {A}},\mathbb {P} )$ ômega– maiúsculo a–maiúsculo pê–maiúsculo.

21 – Definição — Seja uma variável aleatória real no espaço de probabilidade$\scriptstyle \ (\Omega ,{\mathcal {A}},\mathbb {P} )$ omega–maiúsculo a–maiúsculo pê–maiúsculo. Isto é, uma função mensurável $\scriptstyle X:(\Omega ,{\mathcal {A}})\rightarrow (\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))$ função xis–maiúsculo com domínio omega–maiúsculo a–maiúsculo para o contradomínio dos conjuntos reais érre–maiúsculo álgebra de Borel b–maiúsculo do conjunto dos números reais erre–maiúsculo. A distribuição de probabilidade da variável aleatória $\scriptstyle X$ xis–maiúsculo é a medida de probabilidade $\scriptstyle \mathbb {P} _{X}$ pê–maiúsculo subscrito xis–maiúsculodefinida sobre o espaço mensurável $\scriptstyle (\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))$ conjunto dos números reais érre–maiúsculo álgebra de Borel b–maiúsculo do conjunto dos números reais erre–maiúsculo por $\mathbb {P} _{X}(B)=\mathbb {P} {\big (}X^{-1}(B){\big )}=\mathbb {P} (X\in B),$ função probabilidade pê–maiúsculo subscrito xis–maiúsculo de b–maiúsculo igual a função probabilidade de xis–maiúsculo elevado a um negativo de b–maiúsculo igual a função de probabilidade pê–maiúsculo de xis–maiúsculo pertencente a b–maiúsculo para qualquer álgebra de Borel real $\scriptstyle B\in {\mathcal {B}}(\mathbb {R} )$ b–maiúsculo pertencente a b–maiúsculo do conjunto dos números reais erre–maiúsculo. Em outras palavras, $\scriptstyle \mathbb {P} _{X}$ pê–maiúsculo subscrito xis–maiúsculoé a medida de imagem de $\scriptstyle \mathbb {P}$ pê–maiúsculopara $\scriptstyle X$ xis–maiúsculo.

22 – Então, para definir a distribuição de uma variável aleatória, transpõe-se a distribuição de probabilidade $\scriptstyle \mathbb {P}$ pê–maiúsculo de $\scriptstyle \Omega$ ômega–maiúsculo em uma medida $\scriptstyle \mathbb {P} _{X}$ pê–maiúsculo subscrito xis–maiúsculo de $\scriptstyle \mathbb {R}$ érre–maiúsculo.

23 – A representação de uma distribuição por uma variável aleatória não é única. Em outras palavras, duas variáveis aleatórias diferentes ou duas variáveis aleatórias definidas em espaços diferentes podem ter a mesma distribuição. Duas variáveis aleatórias reais $\scriptstyle X$ xis–maiúsculo e $\scriptstyle Y$ ipsilon–maiúsculo têm a mesma distribuição $\scriptstyle \mathbb {P} _{X}=\mathbb {P} _{Y}\$pê–maiúsculo subscrito xis–maiúsculo igual a pê–maiúsculo subscrito ipsilon–maiúsculo (em termos de igualdade de medidas). Isto é, $\scriptstyle \mathbb {P} _{X}(B)=\mathbb {P} _{Y}(B)$ probabilidade pê–maiúsculo subscrito xis–maiúsculo de b–maiúsculo igual a probabilidade pê–maiúsculo subscrito ipsilon–maiúsculo de b–maiúsculo para todo $\scriptstyle B\in {\mathcal {B}}(\mathbb {R} )$ álgebra de Borel b–maiúsculo pertencente a b–maiúsculo do conjunto dos números reais erre–maiúsculo. O seguinte teorema permite uma caracterização adicional.

24 – Teorema de transferência ou de transporte — Seja uma variável aleatória real $\scriptstyle X:\Omega \rightarrow \mathbb {R}$. função xis–maiúsculo com domínio omega– maiúsculo para o contradomínio do conjunto dos números reais érre–maiúsculo Logo $\mathbb {E} \left[\varphi (X)\right]{\stackrel {\text{déf.}}{=}}\int _{\Omega }\varphi {\big (}X(\omega ){\big )}\mathbb {P} (\mathrm {d} \omega )=\int _{\mathbb {R} }\varphi (x)\mathbb {P} _{X}(\mathrm {d} x),$ esperança e–maiúsculo da função phi– minúsculo de xis– maiúsculo igual a integral subscrito omega–maiúsculo da função xis–maiúsculo em função de omega–minúsculo vezes a função de probabilidade pê–maiúsculo da diferencial de omega–minúsculo igual a integral subscrito do conjunto dos números reais erre–maiúsculo da função phi–minúsculo de xis–minúsculo vezes a função de probabilidade pê–maiúsculo subscrito xis–maiúsculo da diferencial de omega–minúsculo para toda função $\scriptstyle \varphi :\mathbb {R} \rightarrow \mathbb {R}$, função phi–minúsculo com domínio dos conjunto dos números reais érre–maiúsculo para o contradomínio do conjunto dos números reais erre–maiúsculo de tal modo que pelo menos uma das duas integrais existe. A última integral, de ponto de vista da teoria da medida, é uma integral da função $\scriptstyle \varphi$ phi–minúsculo em relação da medida $\scriptstyle \mathbb {P} _{X}$ pê–maiúsculo subscrito xis–maiúsculo. Essa integral tem forma de soma, no caso das distribuições discretas. Então, duas variáveis aleatórias reais $\scriptstyle X$ xis–maiúsculo e $\scriptstyle Y$ ipsilon–maiúsculo têm a mesma distribuição se $\scriptstyle \mathbb {E} \left[\varphi (X)\right]=\mathbb {E} \left[\varphi (Y)\right]$ esperança e–maiúsculo da função phi–minúsculo de xis–maiúsculo igual a esperança e–maiúsculo da função phi–minúsculo de ipsilon–maiúsculo para qualquer função $\scriptstyle \varphi :\mathbb {R} \rightarrow \mathbb {R}$ função phi–minúsculo com domínio conjunto dos números reais érre–maiúsculo para o contra–domínio do conjunto dos números reais érre–maiúsculo , tal que existe pelo menos um dos dois termos da igualdade.

25 – Distribuição multidimensional

Distribuição normal bidimensional ou produto de duas distribuições normais unidimensionais.

26 – Uma distribuição de probabilidade é chamada de multidimensional ou $n$-dimensional quando descreve vários valores (aleatórios) de um fenômeno aleatório, por exemplo, no lançamento de dois dados a distribuição de probabilidade dos dois resultados é uma distribuição bidimensional. Então, a característica multidimensional aparece por meio da transferência por uma variável aleatória de um espaço de probabilidade $\scriptstyle (\Omega ,{\mathcal {A}})$ omega–maiúsculo a–maiúsculo para um espaço numérico $\scriptstyle E^{n}$e–maiúsculo elevado a êne–minúsculo , de dimensão $n$. Por exemplo, no lançamento de dois dados a dimensão é $n$ = 2 êne igual a dois e o espaço $\scriptstyle E^{2}$ e–maiúsculo elevado a dois é $\scriptstyle \{1,\dots ,6\}\times \{1,\dots ,6\}$ abre chaves um até seis seis fecha chaves vezes abre chaves um até seis fecha chaves . A distribuição multidimensional também é chamada de distribuição conjunta.

27 – Um exemplo importante da distribuição multidimensional é a probabilidade produto $\scriptstyle \mathbb {P} =\mathbb {P} _{1}\otimes \mathbb {P} _{2}$, probabilidade pê–maiúsculo igual a probabilidade pê–maiúsculo subscrito um multiplicação cartesiana por probabilidade pê–maiúsculo subscrito dois em que $\scriptstyle \mathbb {P} _{1}$ 'pê–maiúsculo subscrito um' e $\scriptstyle \mathbb {P} _{2}$ ê–maiúsculo subscrito dois são duas distribuições unidimensionais. Essa distribuição de probabilidade é uma distribuição de um par de variáveis aleatórias independentes.Esse é o caso do exemplo do lançamento de dois dados.

28 – Definição — Seja uma variável aleatória $\scriptstyle X$ xis–maiúsculo no espaço de probabilidade $\scriptstyle (\Omega ,{\mathcal {A}},\mathbb {P} )$ omega–maiúsculo a–maiúsculo pê–maiúsculo, com valores em $\scriptstyle {\mathbb {R} }^{n}$ conjunto dos números reais erre–maiúsculo elevado a êne–minúsculo equipada com produtos de algebras de Borel $\scriptstyle {{\mathcal {B}}(\mathbb {R} )}^{\otimes n}$ b–maiúsculo pertencente ao conjunto dos números reais érre–maiúsculo elevada ao produto cartesiano de êne–minúsculo . A distribuição da variável aleatória$\scriptstyle \ X\$xis–maiúsculo é a medida de probabilidade $\scriptstyle \mathbb {P} _{X}$ pê–maiúsculo subscrito xis–maiúsculo definida para todo $\scriptstyle B\in {{\mathcal {B}}(\mathbb {R} )}^{\otimes n}$ b–maiúsculo pertencente a álgebra de Borel b–maiúsculo pertencente ao conjunto dos números reais érre–maiúsculo elevada ao produto cartesiano de êne–minúsculo $\mathbb {P} _{X}(B)=\mathbb {P} {\big (}X^{-1}(B){\big )}=\mathbb {P} (X\in B).$função de probabilidade pê–maiúsculo subscrito xis–maiúsculo de b–maiúsculo igual a função de probabilidade de xis–maiúsculo elevado a um negativo de b–maiúsculo igual a função de probabilidade pê–maiúsculo de xis–maiúsculo pertencente a b–maiúsculo

29 – A variável aleatória $\scriptstyle X$ xis–maiúsculo é identificada a um vetor aleatório de dimensões $n$: ene $\scriptstyle X=(X_{1},X_{2},\dots ,X_{n})$xis–maiúsculo igual a abre parênteses, xis–maiúsculo um xis–maiúsculo dois e assim sucessivamente até xis–maiúsculo ene fecha parêntesis. O teorema de Cramer-Wold estabelece que a distribuição ($n$-dimensional) do vetor aleatório é completamente determinado pelas distribuições (unidimensionais) de todas as combinações lineares dos componentes: $\scriptstyle \sum _{i=1}^{n}a_{i}X_{i}$ somatória de i igual a um até ene do primeiro termo a–minúsculo subscrito i vezes xis–maiúsculo subscrito i para todo $\scriptstyle a_{1},a_{2},\dots ,a_{n}$ a–minúsculo um a–minúsculo dois e assim sucessivamente até a–minúsculo ene

30 – Imagem. Distribuição normal bidimensional ou produto de duas distribuições normais unidimensionais.

31 – Distribuição absolutamente contínua

Ilustração de três esquemas em branco e preto, com uma nuvem de pontos em forma de triângulo à esquerda e duas curvas à direita. Elas representam duas coordenadas (dimensão 1 e dimensão 2) de dois pontos que se aproximam cada uma com uma distribuição normal. Isto é, uma simulação de distribuição bidimensional em que as duas distribuições marginais são normais.

32 – Uma distribuição bidimensional ou $n$-dimensional é chamada de absolutamente contínua em $\scriptstyle \mathbb {R} ^{2}$ conjunto dos números reais érre–maiúsculo elevado a dois quando a distribuição é absolutamente contínua com relação à medida de Lebesgue em $\scriptstyle \mathbb {R} ^{2}$ conjunto dos números reais érre–maiúsculo elevado a dois .Isto é, se a distribuição da variável aleatória correspondente é descrita como $\mathbb {P} (X\in B)=\iint _{B}f_{X}(x_{1},x_{2})\mathrm {d} x_{1}\mathrm {d} x_{2}$ para todo $\scriptstyle B\in {\mathcal {B}}(\mathbb {R} ^{2}).$ função de probabilidade pê–maiúsculo de xis–maiúsculo pertencente a b–maiúsculo igual a integral dupla subscrito b–maiúsculo da função efe–minúsculo subscrito xis–maiúsculo de xis–minúsculo um xis–minúsculo dois vezes a diferencial de xis–minúsculo um vezes a diferencial de xis–minúsculo dois

33 – Distribuição marginal

Ver artigo principal: Distribuição marginal

34 – Uma distribuição marginal de um vetor aleatório é a distribuição dos seus componentes. Para obter-la, projeta-se a distribuição em um espaço unidimensional de uma coordenada desejada. A distribuição de probabilidade da $i$-ésima coordenada de um vetor aleatório é chamada de $i$-ésima distribuição marginal $\scriptstyle \mathbb {P} _{i}$.probabilidade pê–maiúsculo subscrito i A distribuição marginal $\scriptstyle \mathbb {P} _{i}$ probabilidade pê–maiúsculo subscrito i de $\scriptstyle \mathbb {P}$ probabilidade pê–maiúsculo é obtida pela fórmula $\mathbb {P} _{i}(A)=\mathbb {P} _{X_{i}}(A)=\iint {1}_{\omega _{i}\in A}\mathbb {P} (\mathrm {d} (\omega _{1},\dots ,\omega _{n}))$probabilidade pê–maiúsculo subscrito i de a–maiúsculo igual a probabilidade pê–maiúsculo subscrito xis–maiúsculo i de a–maiúsculo igual a integral dupla indefinida de um subscrito ômega–minúsculo subscrito i pertencente a a–maiúsculo vezes a probabilidade pê–maiúsculo da diferencial de omega–minúsculo um até ômega–minúsculo ene para todo $\scriptstyle A\in {\mathcal {B}}(\mathbb {R} )$ a–maiúsculo pertencente a álgebra de Borel b–maiúsculo pertencente ao conjunto dos números reais érre–maiúsculo

35 – As distribuições marginais de uma distribuição absolutamente contínua são expressas com suas densidades marginais.

36 – Imagem. Ilustração de três esquemas em branco e preto, com uma nuvem de pontos em forma de triângulo à esquerda e duas curvas à direita. Elas representam duas coordenadas (dimensão 1 e dimensão 2) de dois pontos que se aproximam cada uma com uma distribuição normal. Isto é, uma simulação de distribuição bidimensional em que as duas distribuições marginais são normais.

37 – Distribuição condicional

Ver artigo principal: Probabilidade condicionada

Ilustração de uma árvore binária de dois andares orientada da esquerda para a direita. Ela representa a aplicação de uma distribuição condicional, em que + significa que o indivíduo é positivo para o teste de drogas e U significa que o indivíduo é usuário de drogas $\mathbb {P} (+|U)$ é a probabilidade de o teste ser positivo para um indivíduo usuário de drogas.

38 – Uma distribuição de probabilidade condicionada permite descrever o comportamento de um fenômeno aleatório quando a informação sobre o processo é conhecida. Em outras palavras, a probabilidade condicionada permite avaliar o grau de dependência estocástica entre dois eventos, por exemplo, no lançamento de dois dados a distribuição condicional pode dar a soma dos resultados sabendo que o resultado do lançamento de um dos dois dados foi pelo menos quatro.

39 – Definição para eventos

40 – A probabilidade condicionada é definida em eventos pela probabilidade $\scriptstyle \mathbb {P} (\cdot |B)$: probabilidade pê–maiúsculo de abre parênteses ponto barra b–maiúsculo fecha parênteses a probabilidade de um evento A qualquer condicionado a um evento B. Para quaisquer A e B da σ-álgebra subjacente tal que $\scriptstyle \mathbb {P} (B)\neq 0$ probabilidade pê–maiúsculo de b–maiúsculo diferente de zero

$\mathbb {P} (A|B)={\frac {\mathbb {P} (A\cap B)}{\mathbb {P} (B)}}.$função probabilidade pê–maiúsculo de a–maiúsculo barra b–maiúsculo igual a razão da probabilidade pê–maiúsculo da intersecção entre a–maiúsculo e b–maiúsculo pela probabilidade pê–maiúsculo de b–maiúsculo

39 – Em probabilidade e em estatística, a distribuição de probabilidade $\scriptstyle \mathbb {P} (\cdot |B)$ probabilidade pê–maiúsculo de abre parênteses ponto barra b–maiúsculo fecha parênteses comumente usada em distribuição da probabilidade total ou no teorema de Bayes.

40 – Imagem. Ilustração de uma árvore binária de dois andares orientada da esquerda para a direita. Ela representa a aplicação de uma distribuição condicional, em que + o símbolo de mais significa que o indivíduo é positivo para o teste de drogas e U significa que o indivíduo é usuário de drogas $\mathbb {P} (+|U)$ probabilidade pê–maiúsculo de abre parênteses símbolo de mais barra u–maiúsculo fecha parênteses é a probabilidade de o teste ser positivo para um indivíduo usuário de drogas.

41 – Definição para variáveis aleatórias

42 – A probabilidade condicionada também é definida para as variáveis aleatórias. Seja uma variável X xis–maiúsculo condicionada a uma variável Y ipsilon–maiúsculo. Quando $\scriptstyle \mathbb {P} (Y=y)\neq 0$ probabilidade pê–maiúsculo de ipsilon–maiúsculo igual a ipsilon–minúsculo diferente de zero, a distribuição de X xis– maiúsculo dado Y = y ipsilon–maiúsculo igual a ipsilon–minúsculo é definida por

$\mathbb {P} (X\in A|Y=y)={\frac {\mathbb {P} (X\in A,Y=y)}{\mathbb {P} (Y=y)}}.$ função de probabilidade pê-maiíusculo de, abre parênteses, xis-maiúsculo pertencente a-maiúsculo-barra- ipsilon-maiúsculo igual a ipsilon-minúsculo, fecha parênteses. Igual a razão da função de probabilidade de, abre parênteses, xis-maiúsculo pertencente a a-maiúsculo vírgula ipsilon-maiúsculo igual a ipsilon-minúsculo, fecha parênteses, por função de probabilidade pê-maiúsculo de ipsilon-maiúsculo igual a ipsilon-minúsculo.

42 – A definição acima não é válida se a distribuição de Y ipsilon–maiúsculo for absolutamente contínua dado que $\mathbb {P} (Y=y)=0$ função de probabilidade pê–maiúsculo de ipsilon–maiúsculo igual a ipsilon–minúsculopara todo y ipsilon–minúsculo. A definição seguinte é válida para quaisquer das duas variáveis aleatórias.

43 – Definição — Seja $(X,Y)$ xis–maiúsculo ipsilon–maiúsculo um par de variáveis aleatórias reais. Há uma distribuição de probabilidade $\mathbb {P} _{X|Y}$ probabilidade pê–maiúsculo subscrito xis–maiúsculo barra ipsilon–maiúsculo, chamada de distribuição condicional de $X$ xis–maiúsculo dado $Y$ ipsilon–maiúsculo ou dado $Y=y$ ipsilon–maiúsculo igual a ipsilon–minúsculo definida pela e para qualquer função limitada boreliana $\varphi$ phi–minúsculo tal que $\mathbb {E} \left[\varphi (X)|Y\right]=\int \varphi (x)\mathbb {P} _{X|Y}(\mathrm {d} x)$ a esperança ê–maiúsculo da função phi–minúsculo de xis–maiúsculo barra ipsilon–maiúsculo igual a integral da função phi–minúsculo de xis–maiúsculo vezes a probabilidade pê–maiúsculo subscrito xis–maiúsculo barra ipsilon–maiúsculo da diferencial de xis–minúsculoquase certamente.

44 – A distribuição também é denotada como ${\mathcal {L}}(X|Y)$ ou ${\mathcal {L}}(X|Y=y)$ função ele–maiúsculo de xis–maiúsculo barra ipsilon–maiúsculo ou função ele–maiúsculo de xis–maiúsculo barra ipsilon–maiúsculo igual a ipsilon–minúsculo A igualdade anterior é uma igualdade entre variáveis aleatórias.

45 – Definição para σ-álgebra

46 – De maneira mais geral, a distribuição de probabilidade é definida a partir da esperança condicional de uma variável aleatória X xis–maiúsculo dada uma σ-álgebra ${\mathcal {G}}$ gê–maiúsculo. Essa esperança condicional é a única variável aleatória ${\mathcal {G}}$-mensurável denotada como $\mathbb {E} \left[X|{\mathcal {G}}\right]$ esperança ê–maiúsculo de xis–maiúsculo barra gê–maiúsculo, satisfazendo $\mathbb {E} \left[Z\mathbb {E} (X|{\mathcal {G}})\right]=\mathbb {E} \left[ZX\right]$ a esperança ê–maiúsculo de zê–maiúsculo vezes a esperança ê–maiúsculo de xis–maiúsculo barra gê–maiúsculo igual a esperança ê–maiúsculo de zê–maiúsculo vezes xis–maiúsculo para todo Z zê–maiúsculo, variável ${\mathcal {G}}$-mensurável. Então, a distribuição condicional é definida por $\mathbb {P} (A|{\mathcal {G}})=\mathbb {E} (1_{A}|{\mathcal {G}})$ função de probabilidade pê de a–maiúsculo barra gê–maiúsculo igual a esperança ê–maiúsculo de um subscrito a–maiúsculo barra gê–maiúsculo , em que $1_{A}$ um subscrito a–maiúsculo é a função indicadora.

47 – Definição para distribuições absolutamente contínuas

48 – No caso das distribuições absolutamente contínuas, existe uma função densidade condicional de uma distribuição em relação a outra e vice-versa. Se $(x,y)\mapsto f(x,y)$ é a densidade da distribuição bidimensional, as duas densidades condicionais são dadas por

$f(x|y)={\frac {f(x,y)}{f_{Y}(y)}}={\frac {f(x,y)}{\int f(x,y)\mathrm {d} x}}$ e $f(y|x)={\frac {f(x,y)}{f_{X}(x)}}={\frac {f(x,y)}{\int f(x,y)\mathrm {d} y}}$. função éfe–minúsculo de xis–minúsculo barra ipsilon–minúsculo igual a razão da função éfe–minúsculo de xis–minúsculo ipsilon–minúsculo pela função efe–minúsculo subscrito ipsilon–maiúsculo de ipsilon–minúsculo igual a razão da função éfe–minúsculo de xis–minúsculo ipsilon–minúsculo pela integral da função éfe–minúsculo de xis–minúsculo e ipsilon–minúsculo diferencial de xis–minúsculo e função éfe–minúsculo de ipsilon–minúsculo barra xis–minúsculo igual a razão da função éfe–minúsculo de xis–minúsculo e ipsilon–minúsculo pela função éfe–minúsculo subscrito xis–maiúsculo de xis–minúsculo igual a função éfe–minúsculo de xis–minúsculo ipsilon–minúsculo pela integral da função éfe–minúsculo de xis–minúsculo ipsilon–minúsculo diferencial de ipsilon–minúsculo

49 –$f_{X}$ éfe–minúsculo subscrito xis–maiúsculo e $f_{Y}$ éfe–minúsculo subscrito ipsilon– maiúsculosão as duas distribuições marginais de X xis–maiúsculo e Y ipsilon–maiúsculo , respectivamente. Em substituição das integrais pelas somas, obtém-se fórmulas semelhantes quando as distribuições marginais são discretas ou quando a distribuição marginal de X xis–maiúsculo é discreta e de Y ipsilon–maiúsculoé absolutamente contínua ou vice-versa.

50 – Distribuição com valores em um espaço de Banach

51 – Porque $\scriptstyle \mathbb {R}$ erre–maiúsculo é um espaço de Banach, as distribuições dos valores em um espaço de Banach são generalizações das distribuições dos valores reais. A definição é semelhante.

52 – Definição — Seja$\scriptstyle \ X\$xis–maiúsculo uma variável aleatória em um espaço de probabilidade$\scriptstyle \ (\Omega ,{\mathcal {A}},\,\mathbb {P} )$ omega–maiúsculo, a–maiúsculo, pê–maiúsculo com valores em um espaço de Banach $\scriptstyle E$ ê–maiúsculo com σ-álgebra $\scriptstyle {\mathcal {B}}$ b–maiúsculo de Borel gerada pelos conjuntos abertos de $\scriptstyle E$ ê–maiúsculo. A distribuição de probabilidade da variável aleatória$\scriptstyle \ X\$xis–maiúsculo e a medida de probabilidade $\scriptstyle \mathbb {P} _{X}\$probabilidade pê–maiúsculo subscrito xis–maiúsculo definida pelo espaço mensurável$\ (E,{\mathcal {B}})$ ê–maiúsculo b–maiúsculo por $\mathbb {P} _{X}(B)=\mathbb {P} \left(X^{-1}(B)\right)=\mathbb {P} \left(X\in B\right),$ probabilidade pê–maiúsculo subscrito xis–minúsculo de b–maiúsculo igual a função de probabilidade pê–maiúsculo de xis–maiúsculo elevado a um negativo de b–maiúsculo igual a probabilidade pê–maiúsculo de xis–maiúsculo pertencente a b–maiúsculo para todo $\scriptstyle B\in {\mathcal {B}}$ b–maiúsculo pertencente e b–maiúsculo de Borel.

51 – Para obter boas propriedades, é comum considerar as medidas de probabilidade tight. Isto é, Intuitivamente, são as medidas concentradas em seu espaço compacto e com a suposição que o espaço de Banach é separável.

52 – Um possível exemplo do espaço de Banach é o espaço das funções contínuas $\scriptstyle {\mathcal {C}}(\mathbb {R} ^{+},\mathbb {R} )$ c em função do conjunto dos números reais positivos erre–maiúsculo símbolo de mais conjunto dos números reais érre–maiúsculo . Um processo estocástico de uma família de variáveis aleatórias $\scriptstyle (X_{t})_{t\in T}$ xis–maiúsculo subscrito tê–minúsculo para t–minúsculo pertencente a tê–maiúsculo indexadas por conjunto de índices T tê–maiúsculo. Uma definição possível da distribuição de probabilidade de tal processo é chamada de distribuição finita-dimensional. Isto é, a distribuição multidimensional dos vetores $\scriptstyle (X_{t_{1}},X_{t_{2}},\dots ,X_{t_{n}})$ abre parêntesis xis–maiúsculo tê-um xis–maiúsculo tê–dois e assim sucessivamente até xis–maiúsculo tê–ene fecha parêntesis quando $\scriptstyle t_{1},t_{2},\dots ,t_{n}\in T$ tê–minúsculo um, tê–minúsculo dois e assim sucessivamente até tê–minúsculo ene pertencente a tê–maiúsculo . Então, a distribuição pode ser estendida pelo teorema da extensão de Carathéodory para todo o processo. Um exemplo é movimento browniano $\scriptstyle (B_{t})_{t\in \mathbb {R} _{+}}$b–maiúsculo subscrito tê–minúsculo para tê-minúsculo pertencente ao conjunto dos positivos símbolo de mais (trajetórias contínuas), cuja distribuição de probabilidade é a medida de Weiner geralmente denotada por $W(A)=\mathbb {P} ((B_{t})_{t\geq 0}\in A)$ função w–maiúsculo de a–maiúsculo igual a função de probabilidade pe–maiúsculo de b–maiúsculo subscrito te–minúsculo para te–minúsculo maior ou igual a zero pertencente a a–maiúsculo para todo subconjunto A a–maiúsculo de $\scriptstyle {\mathcal {C}}(\mathbb {R} ^{+},\mathbb {R} )$. c em função do conjunto dos números reais positivos erre–maiúsculo símbolo de mais conjunto dos números reais érre–maiúsculo

53 – Espaço de distribuições de probabilidade

54 – Uma distribuição de probabilidade é uma medida de massa total unitária. O conjunto de distribuições de probabilidade é um sub-espaço do espaço de medidas finitas. Esse espaço é muitas vezes denominado $\scriptstyle {\mathcal {P}}(\mathbb {R} )$ pê–maiúsculo em função do conjunto dos números reais erre–maiúsculo ou $\scriptstyle {\mathcal {M}}_{1}(\mathbb {R} )$ m–maiúsculo-um em função do conjunto dos números reais erre–maiúsculo pelas distribuições de probabilidade reais. No restante da seção, as propriedades desse espaço são detalhadas para as distribuições de probabilidade em reais. Embora também possam ser detalhadas para distribuições em espaços de Banach.

55 – É possível fornecer esse espaço com uma topologia chamada topologia fraca. Essa topologia define uma convergência fraca das distribuições de probabilidade: uma sequência de distribuições de probabilidade $\scriptstyle (\mathbb {P} _{n},n=1,2,\dots )$ pê–maiúsculo subscrito ene–minúsculo quando êne–minúsculo pertence ao conjunto dos números naturais um dois e assim sucessivamente converge fracamente para uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ pê–maiúsculo se $\lim _{n\rightarrow \infty }\int \varphi (\omega )\mathbb {P} _{n}(\mathrm {d} \omega )=\int \varphi (\omega )\mathbb {P} (\mathrm {d} \omega )$ limite quando ene–minúsculo tende ao infinito da integral da função phi–minúsculo de ômega–minúsculo vezes a função de probabilidade pê–maiúsculo subscrito êne–minúsculo da diferencial de omega–minúsculo for gual a integral da função phi–minúsculo de omega–miúsculo vezes a função de probabilidade pê–maiúsculo da diferencial de omega–minúsculo para toda função contínua $\varphi$ phi–minúsculo de um conjunto limitado.

56 – A convergência é denominada $\scriptstyle \mathbb {P} _{n}{\xrightarrow {w}}\mathbb {P}$.probabilidade pê–maiúsculo subscrito êne tende infinitamente a probabilidade pê–maiúsculo Essa convergência é refletida pelo teorema de transferências de variáveis aleatórias $\scriptstyle (\mathbb {X} _{n},n=1,2\dots )$ xis–maiúsculo subscrito êne–minúsculo quando êne–minúsculo pertence ao conjunto dos números naturais um, dois e assim sucessivamente das respectivas distribuições $\scriptstyle (\mathbb {P} _{n},n=1,2,\dots )$ pê–maiúsculo subscrito ene–minúsculo quando êne–minúsculo pertence ao conjunto dos números naturais um dois e assim sucessivamente Então, a convergência de variáveis aleatórias é chamada convergência em distribuição (ou fraca) é denotada $\scriptstyle X_{n}{\xrightarrow {\mathcal {L}}}X$ xis–maiúsculo subscrito êne–minúsculo tende em distribuição ele–maiúsculo para xis–maiúsculo ou $\scriptstyle X_{n}{\xrightarrow {\mathcal {D}}}X$xis–maiúsculo subscrito êne–minúsculo tende em probabilidade de–maiúsculo para xis–maiúsculo O termo convergência fraca das variáveis aleatórias é mais frequentemente utilizada.

57 – O espaço de distribuições de probabilidade com topologia fraca é um espaço métrico, completo e separável (no caso de um espaço de Banach também separável), tornando-se um espaço polonês.

58 – Propriedades

59 – Parâmetros e famílias

60 – Certas distribuições são agrupadas por família em relação a certas propriedades da sua densidade ou da sua função massa de acordo com o número de parâmetros que as definem, chamados de família paramétrica de distribuição de probabilidade.

Ilustração de diferentes curvas de Gauss assimétricas. Ela representa diferentes parâmetros de forma (assimetria) para densidade de probabilidade da distribuição normal assimétrica.

61 – Parâmetros

63 – Os chamados parâmetros de posição influenciam a tendência central da distribuição de probabilidade. Isto é, o valor ou valores em torno dos quais a lei leva seus maiores valores. A esperança, a mediana, a moda, quantils e decils são os exemplos.

Ilustração de diferentes curvas de Gauss. Ela representa diferentes parâmetros de posição ($\scriptstyle \mu$) e parâmetros de escala ($\scriptstyle \sigma$) para densidade de probabilidade da distribuição normal.

64 – Os chamados parâmetros de escalonamento influenciam a dispersão ou o achatamento da distribuição de probabilidade como a variância (momento de segunda ordem), o desvio padrão ou a intervalo interquartil.

65 – Os chamados parâmetros de forma são outros parâmetros relacionados a distribuição de probabilidade. A cauda de uma distribuição de probabilidade real faz parte de sua forma. As caudas da esquerda e da direita são dos tipos $\scriptstyle ]-\infty ,x[$ menos infinito até xis–minúsculo e $\scriptstyle [y,+\infty [$ ipsilon–minúsculo até mais infinito respectivamente. Uma distribuição de probabilidade é chamada de cauda pesada se a medida de probabilidade da cauda $\scriptstyle \mathbb {P} ([y,+\infty [)$ probabilidade pê–maiúsculo de ipsilon–minúsculo até mais infinito tende mais lentamente a 0, quando y vai para infinito, de que que da distribuição normal. Especialmente para qualquer distribuição absolutamente contínua e centrada, essa definição pode ser representada em termos de densidade:

$\lim _{|x|\rightarrow +\infty }f(x)\exp \left({\frac {1}{2}}x^{2}\right)=+\infty$ limite quando o módulo de xis–minúsculo tende para mais–infinito da função de xis–minúsculo vezes o exponencial de meio xis elevado a dois

é uma distribuição com caudas direita e esquerda pesadas.

66 – A assimetria (momento de terceira ordem) é um exemplo de parâmetro de forma, que permite tornar a cauda da direita mais ou menos pesada. A curtose (momento de quarta ordem) é usada para apoiar ou opor-se aos valores próximos da média daqueles que estão mais distantes. Uma distribuição de probabilidade é chamada de mesocúrtica, leptocúrtica ou platicúrtica se a curtose é 0, positiva ou negativa.

67 – Famílias

68 – Uma distribuição é chamada de família exponencial a um parâmetro se sua densidade de probabilidade ou sua função massa depende de apenas uma parâmetro $\scriptstyle \theta$ da seguinte forma:

$f(y)={\begin{cases}a(\theta )b(y)\mathrm {e} ^{-c(\theta )d(y)}&{\text{ se }}\alpha <y<\beta \\0&{\text{ caso contrário.}}\end{cases}}$

'função éfe–minúsculo de ipsilon–minúsculo é igual a função a–minúsculo de teta–minúsculo vezes b–minúsculo de ipsilon–minúsculo vezes ê–minúsculo elevado a menos função cê–minúsculo de teta–minúsculo vezes função de dê–minúsculo de ipsilon–minúsculo quando ipsilon–minúsculo está entre alfa–minúsculo e beta–minúsculo ou função éfe–minúsculo de ipsilon–minúsculo é igual a zero em caso contrário.'

69 – Essa família inclui muitas distribuições clássicas como distribuição normal, distribuição exponencial, distribuição Gamma, distribuição qui-quadrado, distribuição beta, distribuição de Bernoulli, distribuição de Poisson, entre outras.

70 – Uma distribuição é chamada de família potência a dois parâmetros $\scriptstyle \alpha$ 'alpha–minúsculo' e $\scriptstyle \theta$ 'teta–minúsculo' se a densidade:

$f(y)={\begin{cases}\displaystyle \alpha {\frac {y^{\alpha -1}}{\theta ^{\alpha }}}&{\text{ se }}0\leq y\leq \theta \\0&{\text{ caso contrário.}}\end{cases}}$

função éfe–minúsculo de ipsilon–minúsculo é igual a alpha–minúsculo razão de ipsilon–minúsculo elevado a alpha–minúsculo menos um por teta–minúsculo elevado a alpha–minúsculo quando ipsilon–minúsculo é maior ou igual a zero e menor ou igual a teta–minúsculo ou função éfe–minúsculo de ipsilon–minúsculo é igual a zero em caso contrário.

71 – Distribuição direcional

72 – Quando uma distribuição de probabilidade multidimensional representa a direção aleatória de um fenômeno, ela é chamada de direcional. É uma distribuição de um vetor aleatório unitário de dimensão d, em que $\scriptstyle d\geq 2$ de maior ou igual a dois, ou, de maneira equivalente, é uma distribuição de probabilidade na esfera de dimensão d. Uma distribuição direcional de dimensão d pode ser representada por um vetor (d-1-dimensional) em coordenadas polares como as distribuições de von Mises e de Bingham.

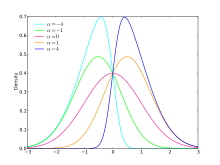
73 – Imagem. Ilustração de diferentes curvas de Gauss. Ela representa diferentes parâmetros de posição ($\scriptstyle \mu$) mi e parâmetros de escala ($\scriptstyle \sigma$) teta para densidade de probabilidade da distribuição normal.

74 – Momentos

Ver artigo principal: Momento (estatística)

75 – Se existir, o n-ésimo momento de uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ pê–maiúsculo é definido como $m_{n}=\int _{\Omega }\omega ^{n}\mathbb {P} (\mathrm {d} \omega )$. emê–minúsculo subscrito êne–minúsculo igual a integral subscrito omega–maiúsculo de omega–minúsculo elevado a ene–minúsculo vezes a probabilidade pê–maiúsculo da diferencial de omega–minúsculo Essa fórmula é descrita simplesmente como $\scriptstyle m_{n}=\mathbb {E} [X^{n}]$ eme–minúsculo subscrito êne–minúsculo igual a esperança ê–maiúsculo de xis–maiúsculo elevado a êne–minúsculo caso a distribuição seja definida a partir de uma variável aleatória $\scriptstyle X$ xis–maiúsculo.

76 – O primeiro momento ou momento de ordem 1 também é chamado de esperança da distribuição. Quando o momento é igual a 0, a distribuição é chamada centrada. O segundo momento ou momento de ordem 2 também é chamado de variância da distribuição. Quando o momento é igual a 1, é dito que a distribuição é reduzida.

77 – De uma maneira geral, a coleção de todos os momentos $\scriptstyle (m_{n},n\in \mathbb {N} )$ ême–minuúsculo subscrito êne–minúsculo quando ene–minúsculo pertence ao conjunto dos números naturais de uma distribuição de probabilidade não é suficiente para caracterizar essa distribuição. Certas distribuições são definidas por um número finito do seu momento: a distribuição de Poisson é completamente definida por sua esperança, a distribuição normal é completamente definida por seus dois primeiros momentos. Certas distribuições não possuem momento como a distribuição de Cauchy.

78 – Entropia

79 – As distribuições de probabilidade permitem representar fenômenos aleatórios. A entropia de Shannon de uma distribuição de probabilidade foi introduzida em termodinâmica para quantificar a desordem molecular de um sistema. O objetivo é medir a falta da informação em lei de probabilidade. A entropia foi definida pela primeira vez para as distribuições discretas, tendo sido estendida para as distribuições absolutamente contínuas. Para uma distribuição discreta $\scriptstyle \mathbb {P} _{1}=\sum _{i\leq n}p_{i}\delta _{x_{i}}$ probabilidade pê–maiúsculo subscrito um igual a somatória com i–minúsculo menor ou igual a êne–minúsculo de pê–minúsculo subscrito i–minúsculo vezes delta–minúsculo subscrito xis–minúsculo subscrito i–minúsculo e uma distribuição $\scriptstyle \mathbb {P} _{2}$ probabilidade pê–maiúsculo subscrito dois de densidade $\scriptstyle f$ éfe–minúsculo, a entropia H h–maiúsculo é definida respectivamente como

$H(\mathbb {P} _{1})=-\sum _{i=1}^{n}p_{i}\log _{2}(p_{i})$ e $H(\mathbb {P} _{2})=-\int _{\mathbb {R} }f(x)\ln(f(x))dx$.

função h–maiúsculo da probabilidade pê–maiúsculo subscrito um igual a menos a somatória com inicio em i–minúsculo até êne–minúsculo de pê–minúsculo subscrito i–minúsculo vezes o logaritmo de base dois de pê–minúsculo subscrito i–minúsculo e função h–maiúsculo da probabilidade pê–maiúsculo subscrito dois igual a menos integral subscrito conjunto dos números reais de função éfe–minúsculo de xis–minúsculo vezes logaritmo natural de função éfe–minúsculo de xis–minúsculo vezes diferencial de xis–minúsculo

• A distribuição normal é a entropia máxima para todas as distribuições possíveis que possuem a mesma média e o mesmo desvio padrão.
• A distribuição geométrica é a entropia máxima para todas as distribuições discretas que possuem a mesma média.
• A distribuição uniforme contínua é a entropia máxima para as distribuições com suporte limitado.
• A distribuição exponencial é a entropia máxima para todas as distribuições em $\scriptstyle \mathbb {R} _{+}$ que possuem a mesma média. 
• As distribuições lei de potência como a lei de Zipf são a entropia máxima entre aqueles que tem o mesma média de logaritmo.

80 – O estado de entropia máxima é o estado mais desordenado, mais estável e mais provável de um sistema. Essas leis são os menos evitável de todas as leis compatíveis com as observações ou condições, e, portanto, a única forma objectiva qualifica-las como distribuições de probabilidade a priori. Essa propriedade tem um papel importante na inferência bayeseana.

Classificação das distribuições de probabilidade na reta real

Representação de três funções de distribuição de distribuições de probabilidade: * em vermelho: distribuição absolutamente contínua (normal padrão); * em azul: distribuição discreta (distribuição de Poisson de parâmetro 2); * em preto: distribuição mista (combinação linear de uma medida de Dirac -2, uma medida de Dirac -1 e uma distribuição de Cauchy de parâmetros -2 e 1.

Distribuições de probabilidade em aplicações mais comuns são distribuições discretas e distribuições absolutamente contínuas. Entretanto, existem distribuições de probabilidade que não são nem discretas nem absolutamente contínuas.

Distribuições discretas

Definição

Ilustração de linha abscissa preta com três pontos discretos. O suporte da distribuição discreta é composto por {1}, {3} e {7} com probabilidades associadas 0,2, 0,5 e 0,3, respectivamente.

Uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ é concentrada ou é realizada em um conjunto $\scriptstyle A\in {\mathcal {A}}$ quando $\scriptstyle \mathbb {P} (A)=1$. Uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ é chamada de discreta se um conjunto $A$ é um conjunto finito ou contável.

O elemento $\scriptstyle \omega \in \Omega$ é chamado de átomo de uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ quando$\scriptstyle \{\omega \}\in {\mathcal {A}}$ e $\scriptstyle \mathbb {P} (\{\omega \})\neq 0$. O conjunto de átomos de uma distribuição discreta é finito ou contável. De modo geral, essa propriedade é válida para toda medida $\sigma$-finita. Para uma distribuição de probabilidade real, o conjunto de átomos é exatamente o conjunto de pontos de descontinuidade de sua função de distribuição. Neste caso, a finitude do conjunto de átomos é dada a partir do fato que a função de distribuição é limitada.

Um critério suficiente para uma distribuição de probabilidade ser discreta é que $\scriptstyle \Omega$ seja finito ou contável.

Se $\scriptstyle \mathbb {P}$ é discreto, então ele se concentra em particular no conjunto (finito ou contável) dos seus átomos $\scriptstyle \Omega _{a}$. Para definir $\scriptstyle \mathbb {P}$ é preciso definir o conjunto dos pares: $\{(\omega ,p(\omega ))\in \Omega _{a}\times ]0,1]\}$, em que $p$ é a função de massa de $\scriptstyle \mathbb {P}$. Então, obtém-se

$\mathbb {P} =\sum _{\omega \in \Omega _{a}}p(\omega )\delta _{\omega }$,

em que $\scriptstyle \delta _{\omega }$ é a medida de Dirac no ponto $\scriptstyle \omega \in \Omega _{a}$.

No caso em que a distribuição de probabilidade é definida a partir de uma variável aleatória, os conceitos anteriores são usados para a variável aleatória: uma variável aleatória $X$, concentrada em conjunto $B\in {\mathcal {B}}(\mathbb {R} )$, é discreta, se a distribuição $\mathbb {P} _{X}$ concentrada em $B$, é discreta. Os mesmo átomos de $\scriptstyle X$ são os átomos de $\scriptstyle \mathbb {P} _{X}$.

Para uma variável aleatória discreta $\scriptstyle X$, o teorema de transferência é expresso na forma de somas ou de séries

$\mathbb {E} \left[\varphi (X)\right]=\sum _{x\in \Omega _{a}}\varphi (x)p_{X}(x)$, para toda função $\scriptstyle \varphi :\mathbb {R} \longrightarrow \mathbb {R}$,

$\mathbb {P} (X\in A)=\sum _{k\in A}\mathbb {P} (X=k)$, para todo $\scriptstyle A\in {\mathcal {B}}(\mathbb {R} )$.

Geralmente a função de distribuição de uma distribuição discreta é constante seccionalmente. Uma distribuição discreta pode ser representada por um gráfico de barras.

Exemplos

Segue uma lista de distribuições de probabilidade discretas com suportes finitos ou contáveis.

Medida de Dirac

A medida de Dirac é o exemplo mais simples das distribuições discretas no sentido de que o suporte possui apenas um valor. Se uma variável aleatória é a medida de Dirac $\delta _{a}$, então $X$ é igual a $a$ com probabilidade igual a 1. Essa lei modela um fenômeno determinista (não aleatório) pois o resultado da experiência é quase certamente igual ao valor conhecido $a$.

Função de distribuição de probabilidade da variável aleatória X	Esperança (1º momento)	Variância (2º momento)	Notação
$F(x)=\left\{{\begin{array}{ll}0,&{\mbox{ se }}x<a\\1,&{\mbox{ se }}x\geq a\end{array}}\right.$	$E[X]=a$	$Var(X)=0$	$\delta ({\vec {x}}-{\vec {x_{o}}})=\delta (x_{1}-x_{1o})\delta (x_{2}-x_{2o})...\delta (x_{n}-x_{no})$

Distribuição uniforme discreta

A distribuição uniforme discreta modela um fenômeno aleatório cujos resultados são igualmente prováveis. É o caso do lançamento de um dado. Se o suporte $S$ da distribuição é um conjunto de $n$ elementos $\{x_{1},x_{2},\dots ,x_{n}\}$, a distribuição é definida como $\mathbb {P} (X=x_{1})=\mathbb {P} (X=x_{2})=\ldots =\mathbb {P} (X=x_{n})={\frac {1}{n}}.$

Função de distribuição de probabilidade da variável aleatória X	Esperança (1º momento)	Variância (2º momento)	Notação
$F(x)=\sum _{(x_{i}\leq x)}^{}{\frac {1}{k}}={\frac {n(x)}{k}}$	$E[X]={\frac {1}{k}}\sum _{i=1}^{k}x_{i}$	$Var(x)={\frac {1}{k}}{\Bigg \{}\sum _{}^{}x_{i}^{2}-{\frac {{\big (}\sum _{}^{}x_{i}{\big )}^{2}}{k}}{\Bigg \}}$	$f_{X}(x_{i})=P(X=x_{i})={\frac {1}{n}},\forall i=1,2,...,n$

Distribuição de Bernoulli

A distribuição de Bernoulli corresponde a uma experiência com dois resultados (sucesso ou fracasso), que geralmente correspondem aos valores 1 e 0. Essa distribuição depende de um parâmetro $p\in [0,1]$para medir a probabilidade de sucesso, sendo definido por $\mathbb {P} (X=1)=1-\mathbb {P} (X=0)=p.$

Função de distribuição de probabilidade da variável aleatória X	Esperança (1º momento)	Variância (2º momento)	Notação
$P(k)={\begin{cases}q=(1-p)&{\text{para }}k=0\\p&{\text{para }}k=1\end{cases}}$	$E\left(X\right)=p$	${\textrm {Var}}\left(X\right)=p\left(1-p\right)$	Ber(p)

Distribuição binomial

É a distribuição do número de sucessos obtidos depois de $n$ ensaios de Bernoulli independentes de parâmetros $p\in [0,1]$, ou seja, é a distribuição da soma de $n$ variáveis aleatórias independentes da distribuição de Bernoulli de mesmo parâmetro. Essa distribuição com suporte finito é definida por $\mathbb {P} (X=k)={n \choose k}p^{k}(1-p)^{n-k}$ para todo $k\in \{0,1,\dots ,n\}$.

Função de distribuição de probabilidade da variável aleatória X	Esperança (1º momento)	Variância (2º momento)	Notação
$P(k)={n \choose k}p^{k}q^{n-k}$	$\operatorname {E} [X]=np$	$\operatorname {Var} [X]=np(1-p)$	Bin(p,n)

Distribuição aritmética

É uma distribuição que concentra-se em um conjunto do tipo $\{k\cdot d,k\in \mathbb {Z} \}$, em que $d>0$.

Distribuição geométrica

É a distribuição que modela o tempo de espera do primeiro sucesso de uma de ensaios de Bernoulli independentes com probabilidade de sucesso $p\in [0,1]$. É a única distribuição discreta que possui a propriedade de falta de memória. Essa probabilidade com suporte infinito contável é definida por $\mathbb {P} (X=k)=(1-p)^{k-1}p$. para todo $k\in \mathbb {N} ^{*}$.

Função de distribuição de probabilidade da variável aleatória X	Esperança (1º momento)	Variância (2º momento)	Notação
$P(k)=(1-p)^{k-1}p$	$E[X]={\frac {1}{p}}$	$Var(X)={\frac {1-p}{p^{2}}}$	$X\sim Geo(p)$195-197

Distribuição de Poisson

A distribuição de Poisson descreve o comportamento do número de eventos que ocorrem em um espaço determinado de tempo. Essa distribuição com suporte infinito contável depende de um parâmetro $\lambda >0$ e é definida por $\mathbb {P} (X=k)={\frac {\lambda ^{k}}{k!}}\mathrm {e} ^{-\lambda }$ para todo $k\in \mathbb {N}$.

Função de distribuição de probabilidade da variável aleatória X	Esperança (1º momento)	Variância (2º momento)	Notação
$f(k;\lambda )={\frac {e^{-\lambda }\lambda ^{k}}{k!}},$183	$E\left[X\right]=\lambda$	$\operatorname {Var} [X]=\lambda$	Poisson($\lambda$)

Distribuição hipergeométrica

A distribuição hipergeométrica modela uma retirada simultânea de $n$ bolas uma urna contendo uma proporção $pN$ de bolas vencedoras e uma proporção $(1-p)N$ de bolas perdedoras para um número total $N$ de bolas. A distribuição descreve o número de bolas vencedoras extraídas. Essa distribuição com suporte finito depende de três parâmetros $n\in \mathbb {N} ^{*}$, $p\in [0,1]$ e $N\in \mathbb {N} ^{*}$e é definida por

$\mathbb {P} (X=k)={\frac {{pN \choose k}{(1-p)N \choose n-k}}{N \choose n}}$ para todo $k\in \{0,1,\dots ,n\}$.

Em geral fixamos a proporção, por exemplo $m=pN$.

Função de distribuição de probabilidade da variável aleatória X	Esperança (1º momento)	Variância (2º momento)	Notação
$P\{X=i\}={\frac {{m \choose i}{N-m \choose n-i}}{N \choose n}}$200	$E[X]={\frac {nm}{N}}$203	$Var(X)\approx np(1-p)$204	$X\sim Hgeo(M,N,n)$

Distribuição absolutamente contínua

Definição

Uma distribuição de probabilidade real $\scriptstyle \mathbb {P}$ é chamada de absolutamente contínua ou densidade quando ela é absolutamente contínua em relação a medida de Lebesgue. Se $\scriptstyle \mathbb {P}$ é absolutamente contínua, então, de acordo com teorema de Radon-Nikodym, ela possui uma densidade de probabilidade em relação a medida de Lebesgue. Isto é, existe uma única (em relação a medida zero de Lebesgue) função mensurável positiva $\scriptstyle f:\mathbb {R} \rightarrow \mathbb {R} _{+}$ de tal modo que para qualquer $\scriptstyle A\in {\mathcal {B}}(\mathbb {R} )$: $\mathbb {P} (A)=\int _{A}f(x)\,\mathrm {d} x=\int _{\mathbb {R} }\mathbf {1} _{A}(x)f(x)\,\mathrm {d} x$, em que $\scriptstyle \mathbf {1} _{A}$ é a função característica de Borel $\scriptstyle A$. Essa densidade de probabilidade nem sempre tem a expressão analítica (ver os exemplos abaixo).

A curva vermelha é a densidade de probabilidade da distribuição normal padrão, chamada de curva de Gauss ou sino.

Quando uma distribuição de probabilidade absolutamente contínua é definida a partir de uma variável aleatória $\scriptstyle X$, a variável aleatória é chamada absolutamente contínua ou densidade e a densidade da distribuição $\scriptstyle \mathbb {P} _{X}$ é igualmente chamada densidade de $\scriptstyle X$, às vezes denotada $\scriptstyle f_{X}$.

Para uma variável aleatória absolutamente contínua $\scriptstyle X$, o teorema da transferência é escrita por meio de uma integral de Lebesgue para toda função $\scriptstyle \varphi :\mathbb {R} \longrightarrow \mathbb {R}$ integral em relação a medida $\scriptstyle \mathbb {P} _{X}(\mathrm {d} x)=f_{X}(x)\,\mathrm {d} x$: $\mathbb {E} \left[\varphi (X)\right]=\int _{\mathbb {R} }\varphi (x)f_{X}(x)\,\mathrm {d} x.$

A função de distribuição de uma distribuição absolutamente contínua é localmente absolutamente contínua, uma propriedade necessária e suficiente. Uma distribuição absolutamente contínua não possua átomos. Entretanto, essa propriedade que opõe-se as distribuições absolutamente contínuas às distribuições discretas não é característica das distribuições absolutamente contínuas mas as leis contínuas (ver a seção distribuições singulares abaixo).

As distribuições absolutamente contínuas também são chamadas de distribuições contínuas. Este é um equívoco, porque na maioria das aplicações Estatística as distribuições contínuas são absolutamente contínuas, mas isso não é verdadeiro no caso geral.

Exemplos

Distribuição uniforme

Intuitivamente uma distribuição uniforme sobre um intervalo indica que todos os valores do intervalo tem a mesma chance de aparecer. Mais formalmente cada subintervalo $\scriptstyle [c,d]\subset [a,b]$ tem uma probabilidade igual a medida de Lebesgue de $\scriptstyle [c,d]$ (multiplicado por uma constante). A distribuição uniforme depende apenas do intervalo, o seu suporte é compacto e a sua densidade é dada pela:

$f(x)={\frac {1}{b-a}}$ para $x\in [a,b]$.

$f(x)=0$ se não.

Distribuição de probabilidade da variável aleatória X (densidade)	Esperança (1º momento)	Variância (2º momento)	Notação
$f(x,\alpha ,\beta )=\left\{{\begin{matrix}{\frac {1}{\beta -\alpha }},&{\mbox{se }}\alpha \leq x\leq \beta \\0,&{\mbox{caso contrário}}\end{matrix}}\right.$	$\mathrm {E} [X]={\frac {\alpha +\beta }{2}}$	$\mathrm {Var} [X]={\frac {(\beta -\alpha )^{2}}{12}}$	$X\sim U(\alpha ,\beta )$

Distribuição exponencial

A distribuição exponencial é comumente usada para modelar o tempo de vida de um fenômeno pois é a única distribuição absolutamente contínua com propriedade de falta de memória. Ela pode ser considerada como um análogo continuo de distribuição geométrica. Essa distribuição com suporte semi-infinito depende de um parâmetro $\lambda$ (às vezes chamado de intensidade), em que a densidade é definida como $f(x)=\lambda \mathrm {e} ^{-\lambda x}$ para todo $\scriptstyle x\geq 0$.

Distribuição de probabilidade da variável aleatória X (densidade)	Esperança (1º momento)	Variância (2º momento)	Notação
$f(x,\lambda )=\left\{{\begin{matrix}\lambda e^{-\lambda x},&{\mbox{se }}x\geq 0\\0,&{\mbox{caso contrário}}\end{matrix}}\right.$	$\mathrm {E} [X]={\frac {1}{\lambda }}$	$\mathrm {Var} [X]={\frac {1}{\lambda ^{2}}}$	$X\sim Exp(\beta )$

Distribuição normal

Uma distribuição normal ou distribuição gaussinana é uma distribuição central na teoria da probabilidade. Ela descreve o comportamento de séries de experiências aleatórias quando o número de tentativas é muito grande. É a distribuição limite do teorema central do limite. Ela é igualmente a única distribuição estável de parâmetro 2. A distribuição normal é caracterizada por sua média (que também é sua mediana) e seu desvio-padrão, com suporte da toda reta real. Sua densidade $f(x;\mu ,\sigma ^{2})$é simétrica e sua forma é comumente chamada de curva de Gauss ou curva em sino.

Distribuição de probabilidade da variável aleatória X (densidade)	Esperança (1º momento)	Variância (2º momento)	Notação
$f(x;\mu ,\sigma ^{2})={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{\frac {-(x-\mu )^{2}}{2\sigma ^{2}}},$ $x\in \mathbb {R}$	$\mathrm {E} [X]=\mu <\infty$	$\mathrm {Var} [X]=\sigma ^{2}<\infty$	$X\sim N(\mu ,\sigma ^{2})$

Distribuição de Cauchy

A distribuição de Cauchy é a distribuição estável de parâmetro 1, o que dá as boas propriedades. Entretanto, é um exemplo típico de distribuição que não admite momentos, em particular nem média nem variância. Com suporte da toda reta real a sua densidade $f(x;\theta )$ é simétrica.

Distribuição de probabilidade da variável aleatória X (densidade)	Esperança (1º momento)	Variância (2º momento)	Notação
$f(x;\theta )={\frac {1}{\pi }}{\frac {1}{\left[1+(x-\theta )^{2}\right]}},$ $x,\theta \in \mathbb {R}$	Não existe (é infinita)	Não existe (é infinita)	$X\sim Cau(\mu ,\sigma )$

A distribuição da posição de um movimento browniano no plano quando se atinge a reta $\scriptstyle y={\frac {1}{2}}$ é uma distribuição de Cauchy.

Distribuição de Tukey-Lambda

Uma distribuição de Tukey-Lamba é uma distribuição absolutamente contínua. Logo possui uma densidade de probabilidade, mas não possui uma expressão analítica. Essa distribuição depende de um parâmetro $\lambda$ e é definida a partir da função quantil $Q(p)$.

Distribuição de probabilidade da variável aleatória X (densidade)	Esperança (1º momento)	Variância (2º momento)	Notação
$Q(p)={p^{\lambda }-(1-p)^{\lambda } \over \lambda }$		${\frac {1}{\lambda _{2}^{2}}}(A_{2}-A_{1}^{2})$

Distribuições singulares

Definição

Uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ é chamada de contínua ou difusa quando não possui nenhum átomo.

Em particular, as distribuições absolutamente contínuas são contínuas mesmo que o inverso não seja verdadeiro. A função de distribuição de uma distribuição contínua ser contínua é uma propriedade necessária e suficiente.

Uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ é chamada de singular quanto ela é contínua, mas não absolutamente contínua. Isto é, quando uma distribuição singular não possui nem átomo nem densidade. Esses conceitos também valem para as distribuições de probabilidade definidas a partir de variáveis aleatórias: uma variável aleatória $\scriptstyle X$ é contínua ou difusa, respectivamente singular, quando a distribuição de probabilidade associada $\scriptstyle \mathbb {P} _{X}$ é contínua ou difusa, respectivamente singular.

Exemplo

Função de distribuição da distribuição de Cantor.

Distribuição de Cantor

É uma distribuição singular, definida a partir do conjunto de Cantor $\scriptstyle \left\{\sum _{n=1}^{\infty }{\frac {x_{n}}{3^{n}}}\ |\,x_{n}\in \{0,2\}\right\}$. Quando $\scriptstyle X_{n}$ são variáveis aleatórias independentes e identicamente distribuídas de uma distribuição uniforme discreta em $\scriptstyle \{0,2\}$, então $X=\sum _{n=1}^{\infty }{\frac {X_{n}}{3^{n}}}$ é uma variável aleatória da distribuição de Cantor. Essa distribuição de probabilidade descrita como $\scriptstyle \mathbb {P} _{X}=({\frac {1}{2}}\delta _{0}+{\frac {1}{2}}\delta _{2})^{\otimes \mathbb {N} }$ é a distribuição uniforme do conjunto de Cantor. Sua função de distribuição é a escada de Cantor, diferenciável quase em todos pontos e derivada igual a zero em quase todos pontos.

Em aplicações, é raro que uma distribuição contínua contenha uma parte singular. Entretanto, o conjunto de Cantor aparece em exemplos conhecidos como o conjunto de zeros do movimento browniano.

Outros casos

Existem distribuições de probabilidade que não são nem discretas nem absolutamente contínuas nem singulares, às vezes denominadas leis mistas. De um ponto de vista mais geral, toda distribuição de probabilidade $\scriptstyle \mathbb {P}$ pode se decompor em uma combinação linear de uma distribuição contínua $\scriptstyle \mathbb {P} _{\text{c}}$ e de uma distribuição discreta $\scriptstyle \mathbb {P} _{\text{d}}$. O teorema da decomposição de Lebesgue aplicado a $\scriptstyle \mathbb {P} _{\text{c}}$ indica que essa distribuição contínua se decompõe em uma combinação linear de duas distribuições contínua, uma $\scriptstyle \mathbb {P} _{\text{ac}}$ absolutamente contínua com relação à medida de Lebesgue e outra $\scriptstyle \mathbb {P} _{\text{s}}$ singular sem relação à medida de Lebesgue. Então, a decomposição é descrita como $\mathbb {P} =\alpha \mathbb {P} _{\text{d}}+(1-\alpha )\mathbb {P} _{\text{c}}=\alpha \mathbb {P} _{\text{d}}+\beta \mathbb {P} _{\text{ac}}+\gamma \mathbb {P} _{\text{s}}$, em que $\alpha ,\beta ,\gamma \in [0,1]$ e $\alpha +\beta +\gamma =1$. A presença de $\scriptstyle (\alpha ,\beta ,\gamma )$ garante que $\scriptstyle \mathbb {P} (\Omega )=1$.

A seguinte distribuição de probabilidade real de um exemplo de uma distribuição mista obtida com a junção entre a distribuição discreta definida pelos átomos $\scriptstyle \{x_{k},k\in \mathbb {N} \}$ com a função de massa $p$, e a distribuição absolutamente contínua de densidade $\scriptstyle f$ é descrita como $\mathbb {P} (\mathrm {d} x)=\alpha f(x)\,\mathrm {d} x+(1-\alpha )\sum _{k\in \mathbb {N} }p(x_{k})\delta _{x_{k}}(\mathrm {d} x)$ sendo $\scriptstyle \alpha \in ]0,1[$. Sua função de distribuição é uma função contínua por partes, mas não constante por partes como as funções de distribuição das distribuições discretas.

Intuitivamente isso corresponde a um fenômenos aleatório com a distribuição absolutamente contínua. Imagine o aparelho de medida que não pode medir os dados a partir de um certo limiar c. Todas as medidas não detectadas pelo aparelho serão atribuídas a 0: a distribuição será nula em qualquer parte "menor" do que c, em seguida, um salto aparece em singleton c. As medidas seguem a distribuição absolutamente contínua para os valores maiores que c. No exemplo, a função de distribuição é descontínua em c.

Função de distribuição de uma distribuição mista.

Função de distribuição de uma distribuição mista.

Características de uma distribuição de probabilidade

Existem várias funções de variáveis reais ou complexas que determinam exclusivamente as distribuições de probabilidade. Certas propriedades dessas funções permitem deduzir propriedades para as distribuições como o cálculo de momento ou uma expressão da convergência em distribuição.

Utilização da função de distribuição

Função de distribuição de uma distribuição normal padrão.

De acordo com o sistema de Dynkin, os conjuntos $\scriptstyle ]-\infty ,x]$ chamados paralelepípedos ou retângulos geram algebra de Borel $\scriptstyle {\mathcal {B}}(\mathbb {R} )$ que são suficientes para definir uma distribuição de probabilidade dos paralelepípedos. Supõe-se que a distribuição de probabilidade seja real. Isto é, $\scriptstyle (\Omega ,{\mathcal {A}})=(\mathbb {R} ,{\mathcal {B}}(\mathbb {R} ))$.

A função de distribuição de uma distribuição de probabilidade real $\scriptstyle \mathbb {P}$ denotada como $\scriptstyle F$ é a função definida para todo $\scriptstyle x\in \mathbb {R}$ $F(x)=\mathbb {P} {\big (}]-\infty ,x]{\big )}.$

Uma distribuição de probabilidade é caracterizada por sua função de distribuição. Isto é, duas distribuições de probabilidade são iguais se e somente se suas funções de distribuição forem iguais.

Mais genericamente, toda função monótona càdlàg $\scriptstyle F$ é verificável: $\scriptstyle \lim _{x\to -\infty }F(x)=0$ e $\scriptstyle \lim _{x\to \infty }F(x)=1$ são funções de distribuição de uma única distribuição de probabilidade em $\scriptstyle \mathbb {R}$. A distribuição de probabilidade definida a partir de uma função de distribuição é chamada de medida de Lebesgue-Stieltjes.

Uma das vantagens da função é que ela é bem definida para qualquer distribuição de probabilidade. Entretanto, ela nem sempre tem expressão explícita, por exemplo, a função de distribuição de distribuição normal. A função de distribuição às vezes permite o cálculo de distribuições tais que como a distribuição do máximo ou do mínimo de uma amostra e fornece um critério conveniente de convergência de distribuições de probabilidade pelo teorema de Portmanteau.

Utilização da função característica

Função característica de uma distribuição uniforme contínua em [-1,1]. Se a distribuição for simétrica, a função característica será real.

Chamada função característica de uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ e denotada como $\scriptstyle \Phi$ é a simetria da transformada de Fourier de $\scriptstyle \mathbb {P}$. Para todo $\scriptstyle t\in \mathbb {R}$: $\Phi (t)={\mathcal {F}}(\mathbb {P} )(-t)=\int _{\Omega }\mathrm {e} ^{\mathrm {i} t\omega }\,\mathbb {P} (\mathrm {d} \omega ).$

Como o nome sugere, a função característica determina exclusivamente a distribuição. Isto é, duas distribuições de probabilidade são iguais se e somente se suas funções características forem iguais.

Uma das vantagens da distribuição característica é que ela existe para toda distribuição de probabilidade. Usando a fórmula da inversão da transformada de Fourier, a distribuição de probabilidade também é obtida a partir da função característica. A representação das distribuições para as funções características ainda permite caracterizar a convergência das distribuições de probabilidade pelo teorema de Portmanteau.

Nos casos em que a distribuição de probabilidade é definida a partir de uma variável aleatória $\scriptstyle X$, de acordo com o teorema da transferência para todo $\scriptstyle t\in \mathbb {R}$

$\Phi _{X}(t)=\int _{\mathbb {R} }\mathrm {e} ^{\mathrm {i} tx}\,\mathbb {P} _{X}(\mathrm {d} x)=\int _{\Omega }\mathrm {e} ^{\mathrm {i} tX(\omega )}\,\mathbb {P} (\mathrm {d} \omega )=\mathbb {E} \left[\mathrm {e} ^{\mathrm {i} tX}\right].$

Utilização da função geradora de momentos

Função geradora de momentos de uma distribuição uniforme contínua em [-1,1].

A função geradora de momentos de uma distribuição de probabilidade $\scriptstyle \mathbb {P}$ denotada como $\scriptstyle M$ é a simetria da transformada de Laplace de $\scriptstyle \mathbb {P}$. Quando a função $\scriptstyle \omega \mapsto e^{t\omega }$ é integrada em relação à medida $\scriptstyle \mathbb {P}$ para todo $\scriptstyle t\in \mathbb {R}$: $M(t)={\mathcal {L}}(\mathbb {P} )(-t)=\int _{\Omega }\mathrm {e} ^{t\omega }\,\mathbb {P} (\mathrm {d} \omega ).$

A função geradora de momentos determina a distribuição de probabilidade unicamente se essa função existe em um intervalo que contem a origem.

Uma das vantagens da função geradora de momentos é que ela permite encontrar os momentos da distribuições de probabilidade pelas derivadas. Para todo $\scriptstyle k\in \mathbb {N}$, a $k$-ésima derivada da função geradora de momento em 0 é o momento $\scriptstyle k$ da distribuição de probabilidade em que $M^{(k)}(0)=\int _{\Omega }\omega ^{k}\mathbb {P} (\mathrm {d} \omega )$.

A representação das distribuições para a função geradora de momentos também permite caracterizar a convergência das distribuições de probabilidade pelo teorema de Portmanteau.

Nos casos em que a distribuição de probabilidade é definida a partir de uma variável aleatória $\scriptstyle X$, de acordo com o teorema da transferência para todo $\scriptstyle t\in \mathbb {R}$: $M_{X}(t)=\int _{\mathbb {R} }\mathrm {e} ^{tx}\,\mathbb {P} _{X}(\mathrm {d} x)=\int _{\Omega }\mathrm {e} ^{tX(\omega )}\,\mathbb {P} (\mathrm {d} \omega )=\mathbb {E} \left[\mathrm {e} ^{tX}\right]$.

Para as distribuições definidas a partir de variáveis aleatórias, essa função também permite mostrar a independência das variáveis.

Existe um caso particular das distribuições discretas. A função geradora de probabilidades de uma distribuição de probabilidade discreta $\scriptstyle \mathbb {P} =\sum _{k}p_{k}\delta _{k}$ é definida como a esperança da série geradora $\scriptstyle g(t)=\sum _{k}t^{k}p_{k}$ sub a condição da existência desta série. Essa função geradora determina a distribuição de probabilidade unicamente.

Outras características

A função quantil de uma distribuição de probabilidade real $\scriptstyle \mathbb {P}$ denotada como $\scriptstyle Q$ é a função que fornece o quantil da distribuição. Ela é definida como para todo $\scriptstyle p\in ]0,1[$: $Q(p)=\inf\{u\in \mathbb {R} \ |\ F(u)\geq p\}$, em que $\scriptstyle F$ é a função de distribuição de $\scriptstyle \mathbb {P}$.

Exemplos de quantis.

Certas distribuições de probabilidade são mais fáceis de definir pela função quantil. Intuitivamente $Q(p)$ é o valor tal que uma proporção de valores possíveis menor de que esse valor é igual $p$. $\scriptstyle Q({\frac {1}{4}})$, $\scriptstyle Q({\frac {1}{2}})$, e $\scriptstyle Q({\frac {3}{4}})$ são, respectivamente, o primeiro quantil, a mediana e o terceiro quantil da distribuição.

Se $\scriptstyle F$ é bicontínua então $\scriptstyle Q$ é a função recíproca da função de distribuição $\scriptstyle Q=F^{-1}$, sendo que no caso geral também é chamada de função quantil recíproca geradora de $\scriptstyle F$ ou função inversa contínua à direita de $\scriptstyle F$.

Essa função quantil determina a distribuição associada a $\scriptstyle \mathbb {P}$ no sentido que, se $\scriptstyle U$ é uma variável aleatória da distribuição uniforme contínua de [0,1], então $\scriptstyle Q(U)$ é uma variável aleatória da distribuição inicial $\scriptstyle \mathbb {P}$. Essa representação é particularmente útil por simular as distribuições de probabilidade, sendo suficiente então para simular uma distribuição uniforme contínua e aplicar a função quantil (ver seção abaixo sobre simulação de distribuição de probabilidade).

Certas distribuições não são funções de distribuição explícitas, mas são definidas a partir de uma função quantil é um caso da distribuição de Tukey-Lambda.

81 – Utilizações

82 – Frequentemente a distribuição estatística de uma variável em uma população refere-se aos modelos matemáticos da distribuição de probabilidade. Geralmente é interessante estudar o modelo probabilístico por razões práticas e teóricas, de acordo com afirmações acadêmicas. O estudo começa com uma seleção aleatória de diversos valores ou indivíduos. Se o método utilizado for perfeito (se os valores observados são derivados se uma seleção equiprovável), então são variáveis aleatórias e o estudo do fenômeno equivale ao estudo da distribuição de probabilidade.

83 – Simulação de uma distribuição de probabilidade

84 – Para estudar as distribuições de probabilidade, é importante fazer simulações. Em particular, com o uso de computadores. As distribuições de probabilidade são caracterizadas pela função quantil por meio de uma variável aleatória com distribuição uniforme. Em geral, esse método engloba duas etapas: gerar os referidos valores pseudo aleatórios com distribuição uniforme e inverter a função de distribuição da distribuição estudada. Como a segunda etapa não é óbvia para todas as distribuições, outros métodos são utilizados.

“ Qualquer um que considere métodos aritméticos para produzir dígitos está certamente cometendo um pecado. ”

—  John von Neumann

Simulação da distribuição uniforme contínua, mostrando a imperfeição de 10 mil valores pseudo aleatórios pela presença de áreas menos densas.

85 – Simulação da distribuição uniforme

86 – Para obter valores da distribuição uniforme contínua, o computador simula os valores da distribuição uniforme discreta. Podem ser usados vários métodos: os algoritmos aritméticos são método mais simples, enquanto que as tabelas que podem conter mais de um milhão de dados são cada vez menos utilizadas e os processos físicos como a criação de um ruído de fundo são bastante onerosos para a recuperação de dados. Como os algoritmos são deterministas (não aleatórios), os valores obtidos são chamados pseudo aleatórios. Muitos algoritmos foram desenvolvidos para melhorar a independência e a distribuição entre os valores no intervalo $\scriptstyle [0,1]$ zero e um.

87 – Simulação das outras distribuições

88 – Quando a função de distribuição é reversível, usa-se a caracterização pela função quantil. Quando a função de distribuição não é reversível, podem ser usados vários os seguintes métodos: a transformação de Box-Muller simula a distribuição normal, a técnica de rejeição de von Neumann é baseada em um teste estatístico e é aplicável a várias distribuições, dentre outros métodos específicos.

89 – Exemplo

90 – Um exemplo conhecido de utilização de uma simulação de distribuição de probabilidade é o método de Monte Carlo. Por exemplo, para aproximar o valor de $\pi$. O método de Monte Carlos consiste em simular um grande número de valores de acordo com uma distribuição uniforme contínua em $\scriptstyle [0,1]$ zero e um e computar a proporção dos pares $\scriptstyle (x,y)$ xis–minúsculo e ipsilon–minúsculo em que $\scriptstyle x^{2}+y^{2}\leq 1$. xis–minúsculo elevado a dois mais ipsilon–minúsculo elevado a dois menor ou igual a um eEssa proporção aproxima-se de $\scriptstyle {\frac {\pi }{4}}$ pi sobre quatro quando o número de pontos tende ao infinito.

100 – Imagem. Simulação da distribuição uniforme contínua, mostrando a imperfeição de 10 mil valores pseudo aleatórios pela presença de áreas menos densas.

101 – Aproximação de uma distribuição de probabilidade

Ilustração do teorema central do limite. As sequências empíricas são os possíveis valores da soma de $\scriptstyle n$ dados ($\scriptstyle n\in \{1,2,3,4,5\}$) de seis lados lançados aleatoriamente. Quando $\scriptstyle n$ aumenta, os histogramas convergem para a curva de Gauss que é a densidade da distribuição normal.

102 – Várias aproximações de uma distribuição de probabilidade existam usando diferentes métodos descritas acima. Essas são as técnicas usadas geralmente em casos práticos. O primeiro passo é o recolhimento dos dados, que permite construir objetos empíricos como a função de distribuição empírica. Esses objetos empíricos são às vezes chamados de distribuição de probabilidade, mas são realmente leis empíricas chamadas de distribuições estatísticas. Os teoremas limites ou os testes estatísticos permitem finalmente identificar a melhor distribuição de probabilidade que modela o fenômeno aleatório inicial.

“ As probabilidades devem ser consideradas análogas às medidas das grandezas físicas, ou seja, nunca podem ser conhecidas com exatidão, mas apenas podem ser conhecidas com certa aproximação. ”

—  Émile Borel

103 – Função de distribuição

104 – O teste estatístico de Kolmogorov-Smirnov, baseado no teorema de Portmanteau, permite identificar a função de distribuição empírica calculada a partir dos dados de uma função de distribuição de uma distribuição de probabilidade, em função de uma taxa de rejeição. A vantagem da convergência das funções de distribuição é que as funções existem para todas as distribuições de probabilidade. Essa convergência permite particularmente aproximar uma distribuição absoluta contínua de uma série de distribuições discretas.

105 – Convergência de outras funções características

106 – Diferentes teoremas de convergência de variáveis aleatórias permitem construir uma sequência de distribuições de probabilidade que converge para uma determinada distribuição ou uma distribuição como o limite das distribuições de probabilidade. O teorema central do limite coloca a distribuição normal como a distribuição limite. O teorema da continuidade de Paul Lévy refere-se a convergência das funções características.

107 – Imagem. Ilustração do teorema central do limite. As sequências empíricas são os possíveis valores da soma de$\scriptstyle n$ ene dados ($\scriptstyle n\in \{1,2,3,4,5\}$) ene pertence a abre chaves um, dois, três, quatro, cinco fecha chaves de seis lados lançados aleatoriamente. Quando $\scriptstyle n$ ene aumenta, os histogramas convergem para a curva de Gauss que é a densidade da distribuição normal.

Exemplo de Henry em um diagrama quantil-quantil que permite comparar visualmente os quantis empíricos com os quantis teóricos. É a distribuição normal, não adequada.

108 – Regressão quantílica

109 – A regressão quantílica permite aproximar os quantis da distribuição dos quantis empíricos. Isto é, calculados a partir de quaisquer dados. Um teste estatístico pode ser usado para comparar os quantis empíricos (observados) com os quantis da suposta distribuição para modelar o fenômeno estudado. Essa abordagem é particularmente útil por estudar certas distribuições que não são explicitamente conhecidas por sua função densidade ou sua função de distribuição, mas por seus quantis como a distribuição de Tukey-Lambda.

110 – Imagem. Exemplo de Henry em um diagrama quantil-quantil que permite comparar visualmente os quantis empíricos com os quantis teóricos. É a distribuição normal, não adequada.

111 – Testes estatísticos

112 – Vários testes estatísticos existem para comparar duas distribuições. Especificamente, os testes de aderência permitem comparar um distribuição empírica (isto é, calcular a partir de dados baseados em amostras) com uma suposta distribuição de probabilidade para modelar o fenômeno estudado. Os dois principais testes estatísticos são o teste de Kolmogorov-Smirnov que compara as funções de distribuição e o teste de adequação qui-quadrado que compara os efeitos observados com a distribuição qui-quadrado. Os testes com distribuição normal são chamados testes de normalidade.

113 – Os testes de homogeneidade permitem comparar duas distribuições empíricas para verificar se elas pertencem ao mesmo fenômenos ou se elas podem ser modeladas pela mesma distribuição de probabilidade a priori. Esses testes comparam certas propriedades das distribuições empíricas com a propriedade da distribuição a priori. Eles são úteis na prática porque permite comparar não as distribuições inteiras, mas os valores das distribuições: o teste de Fisher estima as variâncias empíricas por meio da distribuição de Fisher, o teste de Student estima a média empírica por meio da distribuição de Student etc.

114 – Exemplos de modelagem

115 – As distribuições de probabilidade são usadas para representar os fenômenos observados. Uma distribuição de probabilidade dita a priori se ela é assumida para modelar os dados recuperados. Os testes estatísticos são realizados para afirmar ou rejeitar a concordância da distribuição de probabilidade com os dados. Em muitas áreas, os métodos evoluíram e melhores distribuições de probabilidade foram criadas para atender os problemas. Segue uma lista com exemplos concretos de modelagem:

• na economia: a bolsa de valores é uma instituição de troca de bens e de títulos mobiliários. É realizado um estudo da evolução histórica dos preços, incluindo a modelagem da variação dos preços, para melhor estimar os preços futuros de um bem ou de um título. Essas variações foram modeladas por uma distribuição normal em um primeiro momento (Louis Bachelier) e melhoradas com distribuições de Pareto estáveis (Benôit Mandelbrot) em um segundo momento. Esses novos modelos sempre procuraram melhorar a percepção de risco desde então.
• em jogos de azar: para jogar na loteria francesa, é possível escolher 6 entre 49 números possíveis. Se os números são escolhidos ao acaso pelos apostadores (isto é, com uma distribuição uniforme discreta), então o número de ganhadores segue uma distribuição de Poisson. Um estudo pode ser realizado porque o número de ganhadores é um dado conhecido. Parece que a escolha não é uniforme, mas que alguns números foram escolhidos mais de que os outros.
• em manutenção: uma boa compreensão da degradação permite melhorar a performance da manutenção. Várias distribuições a priori são usadas para modelar a evolução das fissuras das calçadas: a distribuição exponencial, a distribuição de Weibull, a distribuição log-normal, a distribuição log-logística etc . Para a utilização do método da máxima verossimilhança, a distribuição log-logistica faz parte das distribuições mais adequadas.
• em medicina: para testar a eficácia dos medicamentos, um ensaio clínico é realizado com uma amostra de pacientes. Esse método faz parte da teoria da decisão. Ele consiste em selecionar um paciente para realizar um teste com dois resultados possíveis (sucesso ou fracasso). Isto é, um teste modelado por uma distribuição de Bernoulli. Em seguida, o teste é repetido quantas vezes forem necessárias. Esse é o método de ensaio de Bernoulli. Um método melhor é usar a distribuição hipergeométrica, que permite considerar apenas o conjunto de pacientes previamente definido.
• em meteorologia: em hidrologia, a pluviometria é o estudo da quantidade de água depois de uma chuva em um ponto do solo por um determinado período de tempo. Não há consenso entre a comunidade científica internacional sobre a escolha da distribuição a priori. Uns autores defendem o uso da distribuição log-normal que se ajusta bem aos valores pequenos. Outros autores sugerem o uso da distribuição gama que se ajusta bem aos valores experimentais. O uso da distribuição de Pareto é interessante para representar os valores médios.

116 – Fim da gravação. Materiais adicionais como notas, referências, bibliografias e ligações externas estão disponíveis no artigo original escrito na Wikipédia.

117 – Texto narrado pelo usuário Mariliawikipedia pelo Centro de Pesquisa, Inovação e Difusão em Neuromatemática, com i apoio da Fundação de Amparo à Pesquisa do Estado de São Paulo, para a Wikipédia lusófona. Este áudio está licenciado sob Creative Commons Attribution ShareAlike 4.0 Unported.

118 – Índice

1Definição informal

2Histórico

3Definição matemática

3.1Distribuição multidimensional

3.1.1Distribuição absolutamente contínua

3.1.2Distribuição marginal

3.2Distribuição condicional

3.2.1Definição para eventos

3.2.2Definição para variáveis aleatórias

3.2.3Definição para σ-álgebra

3.2.4Definição para distribuições absolutamente contínuas

3.3Distribuição com valores em um espaço de Banach

3.4Espaço de distribuições de probabilidade

4Propriedades

4.1Parâmetros e famílias

4.1.1Parâmetros

4.1.2Famílias

4.1.3Distribuição direcional

4.2Momentos

4.3Entropia

5Classificação das distribuições de probabilidade na reta real

5.1Distribuições discretas

5.1.1Definição

5.1.2Exemplos

5.2Distribuição absolutamente contínua

5.2.1Definição

5.2.2Exemplos

5.3Distribuições singulares

5.3.1Definição

5.3.2Exemplo

5.4Outros casos

6Características de uma distribuição de probabilidade

6.1Utilização da função de distribuição

6.2Utilização da função característica

6.3Utilização da função geradora de momentos

6.4Outras características

7Utilizações

7.1Simulação de uma distribuição de probabilidade

7.1.1Simulação da distribuição uniforme

7.2Aproximação de uma distribuição de probabilidade

7.2.1Função de distribuição

7.2.2Convergência de outras funções características

7.2.3Regressão quantílica

7.2.4Testes estatísticos

7.3Exemplos de modelagem

8Ver também 9Referências

Ver também

• Axiomas de probabilidade
• Medida
• Probabilidade
• Probabilidade condicionada
• Teoria das probabilidades
• Variável aleatória