Geometria

 Nota: Para outros significados, veja Geometria (desambiguação).

Parte da série sobre
Matemática
História
Áreas Teoria dos números Geometria Álgebra Cálculo e Análise Matemática discreta Lógica matemática e Teoria dos conjuntos Probabilidade Estatística e Teoria da decisão Relação com as ciências Física Química Computação Biologia Linguística Economia Filosofia Educação
Portal da Matemática

Uma ilustração do Teorema de Desargues, um resultado importante nas geometrias euclidiana e projetiva

(P.Oxy. I 29) mostrando um fragmento dos Elementos de Euclides

A geometria (em grego clássico: γεωμετρία; geo- "terra", -metria "medida") é um ramo da matemática preocupado com questões de forma, tamanho e posição relativa de figuras e com as propriedades dos espaços. Um matemático que trabalha no campo da geometria é denominado de geômetra.

A geometria surgiu independentemente em várias culturas antigas como um conjunto de conhecimentos práticos sobre comprimento, área e volume. Por volta do século III a.C., a geometria foi posta em uma forma axiomática por Euclides, cujo tratamento, chamado de geometria euclidiana, estabeleceu um padrão que perdurou por séculos, ainda que não refletisse a matemática de sua época. Arquimedes, por exemplo, desenvolveu técnicas engenhosas para calcular áreas e volumes sem se preocupar com o tratamento axiomático dos Elementos.

A geometria esférica é um exemplo de geometria não-euclidiana. Ela tem aplicações práticas em navegação e astronomia

A partir da experiência, ou, eventualmente, intuitivamente, as pessoas caracterizam o espaço por certas qualidades fundamentais, que são denominadas axiomas de geometria (como, por exemplo, os axiomas de Hilbert). Esses axiomas não são provados, mas podem ser usados em conjunto com os conceitos matemáticos de ponto, linha reta, linha curva, superfície e sólido para chegar a conclusões lógicas, chamadas de teoremas.

A influência da geometria sobre as ciências físicas foi enorme. Como exemplo, quando o astrônomo Kepler mostrou que as relações entre as velocidades máximas e mínimas dos planetas, propriedades intrínsecas das órbitas, estavam em razões que eram harmônicas — relações musicais —, ele afirmou que essa era uma música que só podia ser percebida com os ouvidos da alma — a mente do geômetra.

Com a introdução da geometria analítica, muitos problemas de álgebra puderam ser transformados em problemas de geometria e vice-versa, muitas vezes conduzindo à simplificação das soluções.

História

Egito Antigo

Ver artigo principal: Geometria do Antigo Egito

Ilustração do ensino da Geometria, dos Elementos de Euclides

A matemática surgiu de necessidades básicas, em especial da necessidade econômica de contabilizar diversos tipos de objetos. De forma semelhante, a origem da geometria (do grego geo =terra + metria= medida, ou seja, "medir terra") está intimamente ligada à necessidade de melhorar o sistema de arrecadação de impostos de áreas rurais, e foram os antigos egípcios que deram os primeiros passos para o desenvolvimento da disciplina.

Todos os anos o rio Nilo extravasava as margens e inundava o seu delta. A boa notícia era a de que as cheias depositavam nos campos de cultivo lamas aluviais ricas em nutrientes, tornando o delta do Nilo a mais fértil terra lavrável do mundo antigo. A má notícia consistia em que o rio destruía as marcas físicas de delimitação entre as possessões de terra, gerando conflitos entre indivíduos e comunidades sobre o uso dessa terra não delimitada.

A dimensão desses conflitos pode ser apreciada na repercussão que se encontra no Livro dos Mortos do Egito, onde uma pessoa acabada de falecer tem de jurar aos deuses que não enganou o vizinho, roubando-lhe terra. Era um pecado punível com ter o coração comido por uma besta horrível chamada o «devorador». Roubar a terra do vizinho era considerado uma ofensa tão grave como quebrar um juramento ou assassinar alguém. Sem marcos fronteiriços, os agricultores e administradores de templos, palácios e demais unidades produtivas fundadas na agricultura não tinham referência clara do limite das suas possessões para poderem cultivá-la e pagarem os impostos devidos na medida da sua extensão aos governantes.

Os antigos faraós resolveram passar a nomear funcionários, os agrimensores, cuja tarefa era avaliar os prejuízos das cheias e restabelecer as fronteiras entre as diversas posses. Foi assim que nasceu a geometria. Estes agrimensores, ou esticadores de corda (assim chamados devido aos instrumentos de medida e cordas entrelaçadas concebidas para marcar ângulos retos), acabaram por aprender a determinar as áreas de lotes de terreno dividindo-os em retângulos e triângulos.

A origem da geometria se situar no Egito é muito em função dos trabalhos do antigo historiador Heródoto, que defendia que a geometria teria sido inventada a partir das necessidades práticas, enquanto que os gregos teriam se apropriado dessa geometria e teriam adicionado a argumentação dedutiva e o pensamento abstrato. No entanto, essa tese não é mais sustentada pelos historiadores, uma vez que há diversos outros registros de práticas geométricas em civilizações como na Mesopotâmia Antiga ou no extremo oriente.

Os três problemas clássicos da geometria

Ao longo da história, três problemas se tornaram clássicos: a quadratura do círculo, a duplicação do cubo e a trissecção do ângulo.

Esses problemas se tornaram populares, pois, por muito tempo, acreditava-se que seria possível resolvê-los apenas com régua e compasso, como determina a tradição euclideana. Alguns matemáticos propuseram soluções para tais problemas utilizando outros recursos. De fato, qualquer um dos problemas clássicos da Geometria têm solução trivial por meio da álgebra ou ainda por meio de geometria a partir de curvas mecânicas, como a espiral de Arquimedes, ou outros instrumentos. Somente a partir do século XIX tornou-se aceito pela comunidade matemática a impossibilidade de resolver tais problemas apenas com régua e compasso.

O primeiro problema: A quadratura do círculo

O Problema da Quadratura do Círculo

O problema da quadratura do círculo foi proposto por Anaxágoras (499-428 a.C.): dado um círculo, construir um quadrado de mesma área. Como os gregos desconheciam as operações algébricas e priorizavam a Geometria, propunham solução apenas com régua (sem escala) e compasso.

O segundo problema: A duplicação do cubo

Representação Gráfica do Problema da Duplicação do Cubo

Conta uma lenda que, em 429 a.C., durante o cerco espartano na Guerra do Peloponeso, uma peste dizimou um quarto da população de Atenas, matando inclusive Péricles, e que uma plêiade de sábios fora enviada ao oráculo de Apolo, em Delfos, para inquirir como a peste poderia ser eliminada.

O oráculo respondeu que o altar cúbico de Apolo deveria ser duplicado. Os atenienses celeremente dobraram as medidas das arestas. A peste, em vez de se amainar, recrudesceu. Qual o erro? Em vez de dobrar, os atenienses octuplicaram o volume do altar. A complexidade do problema deve-se ao fato de que os gregos procuravam uma solução geométrica, usando régua (sem escala) e compasso.

Em 1837, Pierre L. Wantzel, um jovem professor e matemático francês de apenas 23 anos, demonstra que a quadratura do círculo e a duplicação do cubo não podem ser resolvidos utilizando-se apenas régua e compasso.

O terceiro problema: A trissecção do ângulo

A trissecção do ângulo foi o terceiro dos problemas clássicos da antiguidade grega. Pretendia-se trissectar um ângulo, isto é, dividi-lo em três partes perfeitamente iguais usando apenas uma régua não graduada e um compasso.

Arquimedes propôs uma solução utilizando a espiral que leva seu nome.

Axiomatização da geometria

Ver artigo principal: Geometria euclidiana

Os gregos antigos desenvolveram uma estrutura de argumentação axiomática para a geometria que ficariam bastante populares na matemática europeia moderna. Essa estrutura que parte de algumas definições, axiomas e postulados e, que a partir desses elementos devidamente pré-estabelecidos, poderiam se deduzir os teoremas da geometria. Por volta do ano 300 a.C., Euclides, um matemático grego que vivia em Alexandria, escreveu um livro em 13 volumes intitulado Os Elementos, que expôs uma matemática de forma sistemática e estruturada, que reflete parte do conhecimento geométrico de diversos matemáticos gregos. Os Elementos, além de geometria, também trata de aritmética.

Estátua de Euclides

É importante ressaltar que Os Elementos não refletem todas práticas matemáticas da Grécia Antiga. A limitação de utilizar somente régua e compasso é uma limitação que só se vê Os Elementos e em alguns outros tratados geométricos desse período. Muitos assuntos matemáticos não foram contemplados nos elementos e muitos matemáticos não lidavam com a matemática a partir de .

Os gregos desenvolviam a matemática não com escopo prático, utilitarista, mas movidos pelo desafio intelectual, pelo “sabor do saber” e pelo prazer intrínseco, já que a matemática enseja o apanágio da lógica, da têmpera racional da mente e da coerência do pensamento. A prática dos debates e da argumentação era comum na vida pública do cidadão grego, portanto isso acaba se refletindo também na geometria.

Alguns influentes historiadores da matemática defendiam que nos Elementos havia teoremas de álgebra ou geometria algébrica, em especial nos livros 2 e 3. No entanto, é importante mencionar que as práticas algébricas são muito posteriores ao período dos gregos antigos. Essa interpretação anacrônica não é mais defendida pelos historiadores de hoje.

Ver também: Matemática da Grécia Antiga

Geometria analítica

Ver artigo principal: Geometria analítica

• 
  Descartes
• 
  Fermat

No século XVII, a criação da geometria analítica pelos matemáticos franceses René Descartes e Pierre de Fermat conectou a álgebra à geometria de forma bastante inovadora. Até então a geometria possuía um papel de justificar os procedimentos algébricos. A álgebra não era vista como uma disciplina, mas como uma extensão da geometria. No entanto, a partir do século XVII, essa hierarquia implícita da superioridade da geometria sobre a álgebra é rompida – ainda que não totalmente até ao século XIX. A álgebra passa a ser utilizada para obter novos resultados geométricos e generalizar outros resultados já conhecidos. As práticas analíticas se tornaram importantes para o desenvolvimento do cálculo infinitesimal.

Geometrias não euclidianas

Ver artigo principal: Geometria não euclidiana

• 
  Gauss
• 
  Bolyai
• 
  Lobachevsky

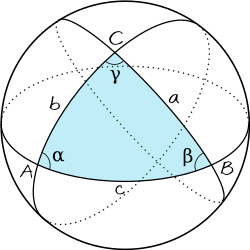
“A suposição de que (em um triângulo) a soma dos três ângulos é menor que 180° leva a uma curiosa geometria, muito diferente da nossa, mas completamente consistente, que desenvolvi para a minha inteira satisfação.” — Carl Gauss

Houve muita controvérsia em torno das geometrias não euclidianas. Por vezes, os teoremas em geometria não euclidiana eram tão exóticos que, apesar de não encontrarem inconsistências lógicas, matemáticos a tomavam como absurda.

O matemático Felix Klein

O matemático Alexander Grothendieck

Programa de Erlangen

Ver artigo principal: Programa de Erlangen

O matemático Benoit Mandelbrot

“Dado qualquer grupo de transformações no espaço que inclui o grupo principal como um subgrupo, então a teoria invariante para esse grupo fornece um tipo definido de geometria, e todas as geometrias possíveis podem ser obtidas dessa mesma maneira.” — Felix Klein

Em 1871, enquanto em Gotinga (Alemanha), Felix Klein fez descobertas importantes em geometria. Klein fez uso da teoria dos invariantes para unir a geometria à teoria dos grupos.^{[carece de fontes]} Ele publicou dois artigos sobre a chamada geometria não euclidiana, mostrando que as geometrias euclidiana e não euclidianas podiam ser consideradas casos especiais de uma superfície projetiva com uma seção cônica específica adjunta. Isso teve o corolário notável de que a geometria não euclidiana era consistente se, e somente se, a geometria euclidiana o fosse, colocando as geometrias euclidiana e não euclidianas em pé de igualdade (uma vez que se fosse encontrada uma inconsistência em qualquer uma delas, isto acarretaria que a outra também é inconsistente), e terminando com toda a controvérsia que girava em torno das geometrias não euclidianas.

Os trabalhos de Grothendieck

No século XX, o matemático Alexander Grothendieck usou teoria das categorias e topologia para generalizar a geometria algébrica, o que lhe permitiu aplicar ferramentas de geometria e topologia à teoria dos números. Essa união é conhecida pelo nome de geometria aritmética.

Os trabalhos de Mandelbrot

Na década de 1960, Benoît Mandelbrot começou a escrever sobre auto-similaridade em artigos tais como "Quão Longa é a Costa da Grã-Bretanha? Auto-Similaridade Estatística e Dimensão Fracionária", e em 1975, ele cunhou o termo fractal, e contribuiu para estimular o campo agora conhecido por geometria fractal.

Ramos

A geometria divide-se em: sintética, convexa, computacional e, discreta

Geometria clássica

De acordo com Henri Poincaré, um espaço geométrico clássico caracteriza-se por possuir as propriedades de ser: contínuo; infinito; tri-dimensional; homogêneo (isto é, com as mesmas propriedades em toda parte); isotrópico (isto é, sem direção privilegiada).

Topologia e geometria

O nó de trevo

O campo da topologia, em que houve enorme desenvolvimento no século XX, é em sentido técnico um tipo de geometria transformacional, em que as transformações que preservam as propriedades das figuras são os homeomorfismos (por exemplo, isto difere da geometria métrica, em que as transformações que não alteram as propriedades das figuras são as isometrias). Isto tem sido frequentemente expresso sob a forma do dito "a topologia é a geometria da folha de borracha".

Geometria diferencial

A geometria diferencial é a disciplina matemática que faz uso de técnicas de cálculo diferencial e cálculo integral, bem como de álgebra linear e álgebra multilinear, para estudar problemas de geometria. Ela é de vital importância no estudo de física teórica.

Geometria algébrica

A geometria algébrica é o ramo da matemática que iniciou como o estudo de sistemas de equações polinomiais em dimensões maiores que 3 e que evoluiu da geometria analítica para uma união de álgebra abstrata, topologia e análise complexa. A demonstração de Andrew Wiles do último teorema de Fermat, um problema de teoria dos números, usou muitas ideias de geometria algébrica descobertas e desenvolvidas a partir do século XX.

Geometria euclidiana

A geometria euclidiana é a geometria em seu sentido clássico. O currículo educacional obrigatório da maioria das nações inclui o estudo de pontos, linhas, planos, ângulos, triângulos, congruência, semelhança, figuras sólidas, círculos e geometria analítica. A geometria euclidiana também possui aplicações em ciência da computação, cristalografia e vários ramos da matemática moderna.

Aplicações

Concha de um nautilus: O formato é aproximadamente uma espiral logarítmica

A geometria surgiu da necessidade de resolver problemas práticos de agricultura, astronomia, arquitetura e engenharia, e de fato, ainda hoje conhecimentos de geometria são aplicados nos mais variados campos do conhecimento humano, tais como: física, química, geologia, astronomia, engenharia, biologia, navegação, cartografia e fotografia. No entanto, cabe ressaltar que a geometria é considerada parte da matemática pura, por, embora tenha começado como uma ciência prática e encontre aplicações em muitos ramos fora da matemática, ela é comumente desenvolvida abstraída da realidade, como uma teoria matemática pela qual matemáticos estudam motivados por seu apelo intrínseco.

Física

Imagens chegam até nós afetadas pelo efeito lente gravitacional

Das observações astronômicas de Kepler (mais tarde explicadas pelos trabalhos de Newton) foi descoberto que os planetas seguem órbitas elípticas com o Sol em um dos focos. As seções cônicas, estudadas pelos gregos antigos encontraram aplicações em mecânica celeste 1800 anos depois de serem por eles descobertas. A linguagem da trigonometria euclidiana é amplamente utilizada no estudo da óptica, em que o conceito de raios de luz pode ser usado para tratar de diversos fenômenos ópticos, como por exemplo, a difração da luz.

Apesar de estudiosos tais como Carl Gauss e Nikolai Lobachevsky terem considerado a possibilidade de o espaço físico não ser euclidiano, as geometrias não euclidianas eram quase que apenas consideradas curiosidades intelectuais abstratas antes de Albert Einstein encontrar usos para elas em teorias de física. Na teoria geral da relatividade, interpreta-se que o espaço torna-se "curvo" na presença de campos gravitacionais.

Química

Molécula cubana do modelo bola e vareta

A geometria de uma molécula (como os átomos que formam uma molécula estão dispostos espacialmente) determina muitas das propriedades químicas e físicas de uma substância. Apesar disso, poucos trabalhos que investigam as relações entre a geometria e química foram realizados por matemáticos:

"É perfeitamente compreensível o fato de os cristalógrafos estarem interessados pelos grupos de simetria de cristais e por outras estruturas tridimensionais, mas é difícil explicar por que este tema tem sido amplamente ignorado pelos matemáticos. Talvez seja uma questão de atitude; os matemáticos há muito tempo consideram como humilhante trabalhar em problemas relacionados com a 'geometria elementar' em duas ou três dimensões, apesar do fato de que é precisamente esse tipo de matemática que é de valor prático." — Branko Grünbaum e G. C. Shephard, em Handbook of applicable mathematics - Volume 5, Parte 2, Página 728.

Projeção ortográfica de uma porção da superfície terrestre

Cartografia

Projeções cartográficas são transformações que mapeiam pontos de uma superfície não plana (geralmente, por simplicidade, assume-se a forma de uma esfera ou elipsoide como o formato do planeta) para os pontos de um plano. É impossível representar a superfície da Terra em um plano sem que ocorram distorções (uma consequência do Theorema Egregium de Gauss).

Engenharia

A geometria fractal é aplicada no projetos de antenas fractais usadas em comunicação sem fio multi-banda compacta — a propriedade de preenchimento do espaço dos fractais é explorada de modo a conseguir-se miniaturizações cada vez mais expressivas. Conhecimentos a respeito de fractais encontram aplicações também no entendimento da porosidade do solo, atrito entre objetos, e em engenharia aeronáutica.

Uma colmeia

Biologia

Já na Antiguidade estudiosos perceberam padrões geométricos na natureza. Papo de Alexandria viveu no século III e escreveu: "As abelhas foram dotadas de uma certa premeditação geométrica .... Pois, havendo apenas três figuras que por elas mesmas pode-se preencher o espaço em volta de um ponto, viz. o triângulo, o quadrado e o hexágono, as abelhas sabiamente escolhem para a sua estrutura aquela que contém o maior número de ângulos, suspeitando de fato que ela pode conter mais mel do que qualquer uma das outras duas".

Curva loxodrómica na esfera

Navegação

A obra do matemático português Pedro Nunes, que viveu no século XVI, voltou-se para o desenvolvimento da teoria náutica e resolução dos problemas que se apresentavam no período das Grandes Navegações Portuguesas, tendo resolvido problemas tais como o de determinar em que longitude se está quando em alto mar, e lançado luz sobre o tema das linhas de rumo (curvas loxodrómicas), extremamente úteis para não se perder a rota quando se navega em alto mar (e, portanto, sem referências costeiras).

Mais exemplos

• 
  A geometria é usada em arte e arquitetura.
• 
  O empacotamento de esferas aplica-se a uma pilha de laranjas.
• 
  Um espelho parabólico concentra raios de luz paralelos em um ponto.

Relações com outros ramos do conhecimento

Como mostrado por Arquimedes, uma esfera tem 2/3 do volume de seu cilindro circunscrito

A matemática é tradicionalmente dividida em três grandes áreas, sendo a geometria uma delas, e a álgebra e a análise as outras duas — que por sua vez se dividem em diversas outras sub-áreas (que frequentemente intersectam-se). Essas três grandes áreas são também conhecidas como delineadoras de maneiras de pensar em matemática, e os matemáticos são por vezes classificados em algebristas, geômetras e analistas. Exemplos de matemáticos considerados geômetras são: Arquimedes, Isaac Newton, Bernhard Riemann, Henri Poincaré, Felix Klein, Michael Atiyah, Vladimir Arnold, e Mikhail Gromov.

Frequentemente a solução para um mesmo problema pode ser encontrada "geometricamente", "algebricamente" ou "analiticamente", e a decisão sobre qual é a melhor, a mais simples, ou a mais adequada solução, frequentemente depende de preferências pessoais bastante subjetivas. Como exemplo, o proeminente matemático russo Vladimir Rokhlin certa vez afirmou bastante emocionado que "a profundidade e a beleza da geometria não podem ser comparadas com as de qualquer outra área da matemática".

Já foram escritos muitos ensaios sobre pensar geometricamente e utilizar intuição geométrica e visualização como poderosos meios de avançar em áreas da matemática, bem como outros com a tese oposta, um fenômeno que frequentemente é descrito como delineador entre as várias escolas de pensamento em matemática, cada qual com prioridades e maneiras de pensar que podem ser eventualmente bastante conflitantes.

Como exemplos, de forma simplificada, mas essencialmente correta: na geometria analítica majoritariamente usa-se álgebra para resolver problemas de geometria, já na álgebra geométrica faz-se o inverso, interpretando-se entes algébricos geometricamente – interpretações geométricas que, por exemplo, podem ser utilizadas para visualizar-se identidades algébricas. As distintas maneiras de se pensar sobre um mesmo tema frequentemente revelam-se nos nomes de alguns dos atuais campo de pesquisa em matemática: topologia algébrica, topologia geométrica e topologia diferencial, bem como teoria dos grupos e teoria geométrica de grupos, e também existem abordagens com apelos mais geométricos, algébricos ou analíticos, em diferentes proporções, em campos que vão de equações diferenciais a sistemas dinâmicos, e muitos outros.

Geometria e análise

A análise é uma ferramenta imprescindível para o estudo aprofundado da geometria. Como exemplo, todos os conceitos básicos em geometria diferencial são definidos por conceitos que pertencem à análise. E o estudo de geometria leva, de maneira natural, a muitos conceitos da análise, tais como os diferentes tipos de derivadas, ao conceito de variedades, e vários outros. Historicamente, foram utilizados muitos artifícios heurísticos na resolução de problemas geométricos cujas justificativas rigorosas pertencem à análise. Também alguns teoremas básicos da geometria necessitam de conceitos da análise para suas demonstrações rigorosas — exemplos disso são o teorema de Tales (que requer a continuidade da reta) e o princípio de Cavalieri (que requer a teoria das integrais por meio de limites).

Simetria como ponte entre diversas áreas

Lilium bulbiferum

A ideia de simetria teve origem no estudo de geometria, e ao longo de sua história, a humanidade foi percebendo a presença de simetrias nas formas presentes na natureza: o sol, as folhas, as flores, os corpos dos humanos e de outros animais, os cristais de gelo, a neve, entre tantos outros exemplos de objetos com formas simétricas. E a medida que eram acumuladas mais observações (sabe-se que a simetria dos cristais de gelo já era bem conhecida na China no século X), cada vez mais a questão de como a simetria surgia na natureza intrigava os estudiosos. Ao longo da evolução da matemática, a noção de simetria se tornou uma das mais importantes noções, não apenas em geometria, mas em todas as áreas da matemática, e também na física —onde o entendimento de simetrias das leis da física fornece meios extremamente eficazes para a compreensão dos fenômenos regidos por tais leis. Os "argumentos de simetria" frequentemente fornecem atalhos e soluções elegantes para problemas matemáticos e físicos. Mas as ideias de simetria são influentes não apenas por fornecerem métodos para a resolução de problemas: o seu aspecto mais importante é que elas são peças-chaves em muitas das ligações entre os diferentes ramos das ciências. (ver também: Teorema de Noether)

Problemas em aberto

Existem muitos problemas em aberto em geometria. Alguns dos quais podem ser entendidos por leigos, por exemplo:

Um triângulo pode ser coberto por três cópias menores de si mesmo, mas um quadrado exige quatro cópias menores.

• Conjectura de Hadwiger: Toda figura convexa n-dimensional pode ser completamente coberta por 2n cópias menores dela mesma? (em aberto desde 1955).
• Conjectura de Toeplitz: Toda curva plana simples fechada contém os quatro vértices de um quadrado? (em aberto desde 1911).
• Conjectura de Erdős–Szekeres: Para n ≥ 3, qualquer conjunto de ⁿ⁻² + 1pontos no plano, em posição geral (disso exclui-se estarem todos alinhados por exemplo), contém n pontos que formam um polígono convexo? (em aberto desde 1935)

Todos os vértices de alguns quadrados fazem parte da curva

Ver também

• Geometria analítica
• Geometria com complexos
• Geometria descritiva
• Geometria esférica
• Geometria euclidiana
• Geometria fractal
• Geometria projetiva
• Projeção ortogonal
• Trigonometria

Ligações externas

• «DPMMS» (PDF) 

Wikiquote

O Wikiquote possui citações de ou sobre: Geometria