Coordenadas polares

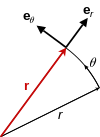
Em matemática, as coordenadas polares são um sistema de coordenadas bidimensional em que cada ponto no plano é determinado por uma distância e um ângulo em relação a um ponto fixo de referência.
O ponto de referência (análogo a origem no sistema cartesiano) é chamado de polo, e a semirreta do polo na direção de referência é o eixo polar. A distância a partir do polo é chamada coordenada radial ou raio, e o ângulo é chamado coordenada angular, ângulo polar ou azimute.[1]
História[editar | editar código-fonte]
Os conceitos de ângulo e raio já eram usados pelas pessoas do primeiro milênio a.C.. O astrólogo e astrônomo grego Hiparco (190 – 120 a.C.) criou uma tabela de funções de corda dando o tamanho da corda para cada ângulo, e existem referências para eles usando coordenadas polares no estabelecimento de posições estelares.[2] Em Sobre as Espirais, Arquimedes descreve a Espiral de Arquimedes, uma função cujo raio depende do ângulo. A matemática grega, no entanto, não se estendeu a um sistema de coordenadas completo.
A partir do século VIII d.C., os astrônomos desenvolveram métodos para aproximar e calcular a direção para Meca (quibla) - e sua distância - de qualquer lugar na Terra.[3]
A partir do século IX d.C passaram a utilizar métodos de trigonometria esférica e projeções cartográficas para determinar estas quantidades com maior precisão. O cálculo é essencialmente a conversão das coordenadas polares equatoriais de Mecca (i.e. sua latitude e longitude) para suas coordenadas polares (i.e. sua quibla e distância) relativa a um sistema cujo meridiano de referência é o círculo máximo através da localização dada e os polos da Terra e cujo eixo polar é a linha entre a localização e o ponto antipodal.[4] Os cálculos eram tão acurados quanto possível sob as condições limitadas impostas pela suposição de que a Terra era uma esfera perfeita.</ref>
Existem diversas referências à introdução das coordenadas polares como parte de um sistema de coordenadas formal. A história completa é descrita em Origin of Polar Coordinates (em tradução livre, Origem das Coordenadas Polares), do professor Julian Lowell Coolidge, da Universidade Harvard.[5] Grégoire de Saint-Vincent e Bonaventura Cavalieri introduziram independentemente os conceitos em meados do século XVII. Saint-Vincent escreveu sobre eles em 1625 e publicou seu trabalho em 1647, enquanto Cavalieri publicou o seu trabalho em 1635 com uma versão corrigida sendo lançada em 1653. Cavalieri primeiramente usou coordenadas polares para resolver um problema relacionado a área dentro da espiral de Arquimedes. Blaise Pascal subsequentemente usou coordenadas polares para calcular o comprimento de arcos parabólicos.
Em Método das Fluxões (escrito em 1671, mas publicado em 1736), Sir Isaac Newton examinou as transformações entre as coordenadas polares, as quais chamou de "Sétima Maneira para Espirais", e outros nove sistemas de coordenadas.[6] No jornal Acta Eruditorum (1691), Jacob Bernoulli usou um sistema com um ponto e uma reta, chamado de polo e eixo polar, respectivamente. As coordenadas eram especificadas pela distância do polo e o ângulo a partir do eixo polar. O trabalho de Bernoulli estendeu-se a achar o raio de curvatura de curvas expressas nessas coordenadas.
O termo coordenadas polares atual tem sido atribuído a Gregorio Fontana e foi usado pelos escritores italianos do século XVIII. O termo apareceu em inglês na tradução de 1816 de George Peacock do livro Cálculo Diferencial e Integral de Lacroix.[7][8] Alexis Clairaut foi o primeiro a pensar em coordenadas polares em três dimensões, e Leonhard Euler foi o primeiro a realmente desenvolvê-las.[5]
Convenções[editar | editar código-fonte]

A coordenada radial é frequentemente denotada por ou (rho) e a coordenada angular por (phi), (theta) ou . A coordenada é especificada como pelo padrão ISO 31-11.
Ângulos em notação polar são geralmente expressos tanto em graus quanto em radianos ( sendo igual a ). Graus são tradicionalmente usados em navegação, agrimensura e muitas outras disciplinas aplicadas, enquanto radianos são mais comuns em matemática e física matemática.[9]
Em muitos contextos, uma coordenada positiva angular significa que o ângulo é medido no sentido anti-horário do eixo.
Na literatura matemática, o eixo polar é frequentemente desenhado horizontalmente e apontando para a direita.
Unicidade das coordenadas polares[editar | editar código-fonte]
Adicionando qualquer número de voltas completas () à coordenada angular não muda a direção correspondente. Também, uma coordenada radial negativa é melhor interpretada como a distância positiva correspondente medida na direção oposta. Assim sendo, um mesmo ponto pode ser expresso por um número infinito de coordenas polares diferentes (,) ou (,), onde é um inteiro qualquer.[10] Além disso, o próprio polo pode ser expresso como para qualquer ângulo .[11]
Onde uma representação única é necessária para algum ponto, é usual limitar a números não negativos e ao intervalo ou (em radianos, ou ).[12] Pode-se escolher um azimute único para o polo, e.g., .
Conversão entre coordenadas polares e cartesianas[editar | editar código-fonte]
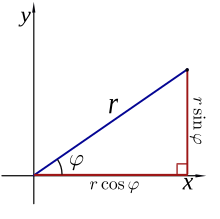

As coordenadas polares e podem ser convertidas para as coordenadas cartesianas e usando as funções trigonométricas seno e cosseno:
As coordenadas cartesianas e podem ser convertidas para as coordenadas polares e com e por:[13]
(como no Teorema de Pitágoras ou na norma euclidiana), e
onde é uma variação comum da função arco tangente definida como
O valor acima de é o valor principal da função número complexo arg aplicada a . Um ângulo no intervalo pode ser obtido adicionando ao valor caso seja negativo.
Equação polar de uma curva[editar | editar código-fonte]
A equação uma curva algébrica expressa em coordenadas polares é conhecida como uma equação polar. Em muitos casos, tal equação pode simplesmente ser especificada ao definir como uma função de . A curva resultante consiste portanto de pondos da forma e pode ser considerada como o gráfico da função polar . Note que, em contrapartida as coordenadas cartesians, a variável independente é o segundo número no par ordenado.
Diferentes formas de simetria podem ser deduzidas da equação da função polar . Se , a curva será simétrica em torno do raio horizontal (0º/180º), se será simétrica em torno do raio vertical (90º/270º) e se será rotacionalmente simétrica em no sentido horário ou no sentido anti-horário em torno do polo.
Por conta da natureza circular do sistema de coordenadas polares, muitas curvas podem ser descritas por uma equação polar simples, enquanto que suas formas cartesianas são muito mais intrincadas. Dentre as mais conhecidas dessas curvas estão a rosa polar, a espiral de Arquimedes, a lemniscata, o limaçon e a cardioide.
Para o círculo, a linha e a rosa polar abaixo, é entendido que não existem restrições no domínio e intervalo da curva.
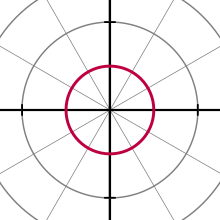
Círculo[editar | editar código-fonte]
A equação geral para um círculo com centro em e raio é:
Isto pode ser simplificado de diversas maneiras, para se adequar a casos mais específicos, tais como a equação
para um círculo com centro no polo e raio .[14] Quando , ou quando a origem se encontra no círculo, a equação se torna
.
No caso geral, a equação pode ser resolvida pra dado
,
a solução com um sinal de menos antes da raiz quadrada dá a mesma curva.

Rosa polar[editar | editar código-fonte]
Uma rosa polar é uma famosa curva matemática que parece como uma flor petalada e que pode ser expressa com uma simples equação polar,
para qualquer constante (incluindo o 0). Se é um inteiro, esta equação produzirá uma rosa k-petalada se for ímpar, ou uma rosa 2k-petalada se for par. Se é racional, mas não inteiro, uma forma semelhante a uma rosa pode ser formada, porém com pétalas sobrepostas. Note que esta equação nunca define uma rosa com 2, 6, 10, 14, ... (). A variável representa o tamanho das pétalas da rosa.
Linha[editar | editar código-fonte]
Linhas radiais (aquelas passando pelo polo) são representadas pela equação
,
onde é o ângulo de elevação da linha; isto é, onde é o declive da linha no sistema de coordenadas cartesiano. A linha não radial que cruza a linha radial que cruza a linha radial perpendicularmente no ponto tem a equação
.
Caso contrário, é o ponto em que a tangente intercepta o círculo imaginário de raio .


Espiral de Arquimedes[editar | editar código-fonte]
A espiral de Arquimedes é uma famosa espiral que foi descoberta por Arquimedes, que pode também ser expressada com uma simples equação polar. É representada pela equação:
Mudar o parâmetro irá virar a espiral, enquanto controla a distância entre os braços, que para uma espiral dada é sempre constante. A espiral de Arquimedes tem dois braços, um para e um para . Os dois braços são conectados suavemente no polo (ver espiral de Fermat). Tomar uma imagem espelhada de um braço através da linha 90º/270º produzirá o outro braço. Essa curva é notável como uma das primeiras curvas, depois das seções cônicas, a serem descritas em um tratado matemático, e como sendo um exemplo primal de uma curva que é mais bem descrita por uma equação polar do que por outros meios.
Seções cônicas[editar | editar código-fonte]
Uma seção cônica com um foco no polo e o outro em algum outro lugar na linha radial de 0º (de modo que o semieixo maior da cônica repouse no eixo polar) é dada por:
onde é a excentricidade e é o semi-lactus rectum (a distância perpendicular em um foco do semieixo maior até a curva). Se , esta equação define uma hipérbole; se , define uma parábola; e se , define uma elipse. O caso especial resulta em um círculo de raio .
Interseção de duas curvas polares[editar | editar código-fonte]
Os gráficos de duas funções polares e têm interseções em 3 casos:
- Na origem das equações e há ao menos uma solução para cada.
- Todos os pontos onde é uma das soluções da equação .
- Todos os pontos onde é uma das soluções da equação onde é um inteiro.
Números complexos[editar | editar código-fonte]


Todo número complexo pode ser representado como um ponto no plano complexo e, portanto, pode ser expressado especificando as coordenadas cartesianas do ponto (chamado de forma retangular ou cartesiana) ou as coordenadas polares do ponto (denominada forma polar). O número complexo pode ser representado de forma retangular como
onde é a unidade imaginária, ou pode ser alternativamente escrito na forma polar (através da fórmula de conversão dada acima) como
e a partir daí como
onde é o número de Euler, que é equivalente como mostrado pela fórmula de Euler.[15] Note que esta fórmula, como todas as outras envolvendo exponenciais de ângulos, assume que o ângulo é expresso em radianos. Para converter entre a forma retangular e forma polar de um número complexo, a fórmula de conversão dada na seção Conversão entre coordenadas polares e cartesianas pode ser usada.
Para as operações de multiplicação, divisão e exponenciação de números complexos, é geralmente muito simples trabalhar com números complexos expressos na forma polar em vez da forma retangular. Para as regras de exponenciação:
- Multiplicação:
- Divisão:
- Exponenciação (Fórmula de De Moivre):
Cálculo[editar | editar código-fonte]
Cálculo pode ser aplicado em equações expressas em coordenadas polares.[16][17]
A coordenada angular é expresso em radianos ao longo dessa seção, que é uma escolha convencional quando se faz cálculo.
Cálculo diferencial[editar | editar código-fonte]
Usando e , pode-se derivar a relação entre derivadas nas coordenadas cartesianas e polares. Para uma função dada, , segue que (computando-se as derivadas totais)
,
ou
,
Consequentemente, tem-se a seguinte fórmula:
Usando a transformação inversa de coordenadas, uma relação análoga e recíproca pode ser obtida através das derivadas. Dada a função , segue que
ou
Consequentemente, tem-se a seguinte fórmula:
Para encontrar a inclinação cartesiana da linha tangente a uma curva polar em qualquer ponto dado, a curva é expressa como um sistema de equações paramétricas
Diferenciando ambas as equações em relação a resulta em
Dividindo a segunda equação pela primeira produz a inclinação cartesiana da linha tangente para a curva no ponto :
Para outras fórmulas úteis que incluem divergência, gradiente e laplaciano em coordenadas polares, veja coordenadas curvilíneas.
Cálculo integral (comprimento de arco)[editar | editar código-fonte]
O comprimento de arco (comprimento de um segmento de linha) definido por uma função polar é encontrado por integração sobre a curva . Deixe denotar esse comprimento ao longo da curva, começando do ponto até o ponto , onde esses pontos correspondem a e , respectivamente, de modo que . O comprimento de L é dado pela seguinte integral
Cálculo integral (área)[editar | editar código-fonte]
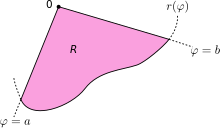
Seja a região contida pela curva e os raios e , onde . Então, a área de é
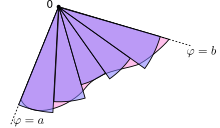

Este resultado pode ser achado como segue. Primeiro, o intervalo é dividido em subintervalos, onde é um positivo inteiro arbitrário. Portanto, (o comprimento de cada subintervalo) é igual a (o tamanho total do intervalo) divido por (o número de subintervalos). Para cada subintervalo , deixe ser o ponto médio do subintervalo, e construa um setor com o centro no polo, de raio e ângulo central e comprimento de arco . A área de cada setor construído é igual a
Consequentemente, a área total de todos os setores é
Conforme o número de subintervalos aumenta, a aproximação da área continua a melhorar. No limite, isto é, com , essa soma se torna uma soma de Riemann para a integral acima.
Um aparelho mecânico que computa a área é o planímetro (figura ao lado), que mede a área de figuras planas ao traçá-las: isto replica a integração em coordenadas polares adicionando uma articulação de modo que a ligação de dois elementos efetua o Teorema de Green, convertendo a integral polar quadrática para uma integral linear.
Generalização[editar | editar código-fonte]
Usando coordenadas cartesianas, um elemento de área infinitesimal pode ser calculado como . A regra de substituição para integrais múltiplas declara que, quando se usa outras coordenadas, o determinante jacobiano da fórmula de conversão de coordenadas tem que ser considerado:
Consequentemente, um elemento de área em coordenadas polares pode ser escrito como
Logo, uma função que é dada em coordenadas polares pode ser integrada como segue:
Aqui, é a mesma região descrita acima, isto é, a região limitada pela curva e os raios e . A fórmula para a área de R mencionada acima é recuperada ao tomar identicamente a 1. Uma aplicação mais surpreendente desse resultado resulta na Integral Gaussiana
Cálculo vetorial[editar | editar código-fonte]
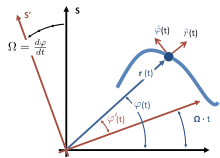
Cálculo vetorial também pode ser aplicado a coordenadas polares. Para movimento planar, seja a posição do vetor , com e dependendo do tempo .
Definem-se os vetores unitários
na direção de e
no plano de movimento perpendicular a direção radial, onde é um vetor unitário normal ao plano de movimento. Então
Termos centrífugo e de Coriolis[editar | editar código-fonte]
O termo é referido às vezes como o termo centrífugo e o termo como o termo de Coriolis.[18] Embora estas equações carreguem alguma semelhança em forma dos efeitos centrífugos e de Coriolis encontrados em referenciais rotativos, essas não são as mesmas coisas.[19] Por exemplo, as forças físicas centrífuga e de Coriolis aparecem somente em referenciais não inerciais. Em contraste, esses termos, que aparecem quando a aceleração é expressa em coordenadas polares, são consequências matemáticas da diferenciação; estes termos aparecem onde quer que coordenadas polares sejam usadas. Em particular, estes termos aparecem mesmo quando coordenadas polares são usadas em referenciais inerciais, onde as forças físicas centrífuga e de Coriolis nunca aparecem.
Referenciais em rotação[editar | editar código-fonte]
Para uma partícula em movimento planar, uma abordagem para atribuir significado físico a esses termos é baseada no conceito de um referencial instantâneo co-rotativo. Para definir um referencial co-rotativo, é selecionada uma origem, a partir da qual é definida a distância até a partícula. Um eixo de rotação é configurado de modo a ser perpendicular ao plano de movimento da partícula e passando por essa origem. Então, no momento selecionado, a taxa de rotação do referencial co-rotativo é construída para coincidir com a taxa de rotação da partícula em relação a este eixo (). Em seguida, os termos na aceleração no referencial inercial estão relacionados a esses termos no referencial co-rotativo. Seja o local a partícula no referencial inercial ser () e no referencial co-rotativo ser (). Porque o referencial rotaciona na mesma taxa que a partícula, . A força centrífuga fictícia no referencial co-rotativo é , radialmente para fora. A velocidade da partícula no referencial co-rotativo também é radialmente para fora, porque . A força de Coriolis fictícia, portanto, tem valor , apontado somente na direção de crescimento de . Assim, usando essas forças na segunda lei de Newton, encontramos:
Onde os pontos sobre a variável representa a segunda derivada de em relação ao tempo e é a força resultante (como oposto as forças fictícias). Em termos de componentes, esta equação vetorial se torna:
- ,
que pode ser comparados as equações para o referencial inercial:
- .
Esta comparação, mais o conhecimento de que por definição o referencial inercial no tempo tem uma taxa de rotação , mostra que podemos interpretar os termos na aceleração (multiplicados pela massa da partícula) como observado no referencial inercial como o negativo das forças centrífugas e de Coriolis que poderiam ser vistas no referencial instantâneo não-inercial co-rotativo.
Para o movimento geral de uma partícula (em oposição ao movimento circular simples), as forças centrífugas e Coriolis no referencial de uma partícula são comumente referidas ao círculo de osculação instantâneo desse movimento, não a um centro fixo de coordenadas polares. Para mais detalhes, veja força centrípeta.
Conexão com coordenadas esféricas e cilíndricas[editar | editar código-fonte]
O sistema de coordenadas polares é estendido para três dimensões com dois sistemas distintos de coordenadas, o sistema cilíndrico e o sistema esférico.
Aplicações[editar | editar código-fonte]
Coordenadas polares são bidimensionais e portanto devem ser usadas somente quando as posições do ponto repousam em um único plano bidimensional. Elas são mais apropriadas em qualquer contexto onde o fenômeno sendo considerado é inerentemente amarrado na direção e tamanho de um ponto central. Por exemplo, os exemplos acima mostram como equações polares elementares são suficientes para definir curvas - tais como a espiral de Arquimedes - cujas equações nas coordenadas cartesianas seriam muito mais intrincadas. Além disso, muitos sistemas físicos - tais como os relacionados ao movimento dos corpos ao redor de um ponto central ou com um fenômeno originado de um ponto central - são simples e mais intuitivos para modelar usando coordenadas polares. A motivação inicial para a introdução do sistema polar foi o estudo de movimento circular e orbital.
[editar | editar código-fonte]
Coordenadas polares são usadas frequentemente em navegação uma vez que o destino ou direção de viagem pode ser dada como um ângulo e distância do objeto sendo considerado. Por exemplo, aeronaves usam uma versão ligeiramente modificada das coordenadas polares para navegação. Nesse sistema, o raio 0º é geralmente chamado de direção 360, e os ângulos continuam no sentido horário, como no sistema matemático. Direção 360 corresponde ao norte magnético, enquanto direções 90, 180 e 270 correspondem ao leste, sul e oeste magnéticos, respectivamente.[20] Portanto, uma aeronave viajando a 5 milhas náuticas para leste estará viajando 5 unidades na direção 90 (pronunciado zero-niner-zero pelo controle de tráfego aéreo).[21]
Modelagem[editar | editar código-fonte]
Sistemas mostrando simetria radial fornecem configurações naturais para o sistema de coordenadas polares, com um ponto central atuando como polo. Um exemplo desse uso é a equação de fluxo de água subterrânea quando aplicada a poços com simetria radial. Sistemas com uma força radial também são bons candidatos para o uso das coordenadas polares. Esses sistemas incluem campos gravitacionais, que obedecem a lei do quadrado inverso, assim como sistemas com fontes pontuais, tais como antenas de radio.
Sistemas com assimetria radial também podem ser modelados com coordenadas polares. Por exemplo, microfones com padrão pickup ilustram a resposta proporcional a um som de entrada de uma direção dada, e estes padrões podem ser representados como curvas polares. A curva para um microfone de padrão cardioide, o microfone unidirecional mais comum, pode ser representada como no desenho da sua frequência alvo.[22] O padrão muda omnidirecionalmente em frequências mais baixas.
Veja também[editar | editar código-fonte]
- Sistema de coordenadas cartesiano
- Sistema de coordenadas cilíndricas
- Sistema de coordenadas esféricas
- Coordenadas geográficas
Referências
- ↑ Brown 1997.
- ↑ Friendly, Michael (24 de agosto de 2009). «Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization» (PDF)
- ↑ King 2005, p. 166 em (Koetsier & Luc 2005, p. 162-178).
- ↑ King 2005, p. 169.
- ↑ a b Coolidge, Julian (1952). «The Origin of Polar Coordinates». Mathematical Association of America. American Mathematical Monthly. 59 (2): 78–85. JSTOR 2307104. doi:10.2307/2307104
- ↑ Boyer, C. B. (1949). «Newton as an Originator of Polar Coordinates». Mathematical Association of America. American Mathematical Monthly. 56 (2): 73–78. JSTOR 2306162. doi:10.2307/2306162
- ↑ Miller, Jeff. «Earliest Known Uses of Some of the Words of Mathematics». Consultado em 10 de setembro de 2006
- ↑ Smith & 1925 324.
- ↑ Serway & Jewett Jr. 2005.
- ↑ «Polar Coordinates and Graphing» (PDF). 13 de abril de 2006. Consultado em 22 de setembro de 2006[ligação inativa]
- ↑ Lee, Cohen & Sklar 2005.
- ↑ Stewart, Tall & Sklar 1983.
- ↑ Torrence & Torrence 1999.
- ↑ Claeys, Johan. «Polar coordinates». Consultado em 25 de maio de 2006. Arquivado do original em 27 de abril de 2006
- ↑ Smith 2003.
- ↑ Husch, Lawrence S. «Areas Bounded by Polar Curves». Consultado em 25 de novembro de 2006
- ↑ Husch, Lawrence S. «Tangent Lines to Polar Graphs». Consultado em 25 de novembro de 2006
- ↑ Shankar 1994, p. 81.
- ↑ Em particular, a taxa de derivação angular aparecendo na expressão da coordenada polar é por conta da partícula sob observação, , enquanto que na mecânica Newtoniana clássica é a taxa angular Ω de um quadro de referência.
- ↑ Santhi, Sumrit. «Aircraft Navigation System». Consultado em 26 de novembro de 2006
- ↑ «Emergency Procedures» (PDF). Consultado em 15 de janeiro de 2007. Arquivado do original (PDF) em 3 de junho de 2013
- ↑ Eargle 2005.
Bibliografia[editar | editar código-fonte]
- Adams, Robert; Essex, Christopher (2013). Calculus: a complete course 8 ed. [S.l.]: Pearson Canada Inc. ISBN 978-0-321-78107-9
- Anton, Howard; Bivens, Irl; Davis, Stephen (2002). Calculus 7 ed. [S.l.]: Anton Textbooks, Inc. ISBN 0-471-38157-8
- Brown, Richard G. (1997). Andrew M. Gleason, ed. Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis. Evanston, Illinois: McDougal Littell. ISBN 0-395-77114-5
- Eargle, John (2005). Handbook of Recording Engineering 4 ed. [S.l.]: Springer. ISBN 0-387-28470-2
- Finney, Ross; Thomas, George; Demana, Franklin; Waits, Bert (1994). Calculus: Graphical, Numerical, Algebraic. [S.l.]: Addison-Wesley Publishing Co. ISBN 0-201-55478-X
- King, David A. (2005). The Sacred Geography of Islam. [S.l.: s.n.]
- Koetsier, Teun; Luc, Bergmans (2005). Mathematics and the Divine: A Historical Study. Amsterdam: Elsevier. ISBN 0-444-50328-5
- Lee, Theodore; Cohen, David; Sklar, David (2005). Precalculus: With Unit-Circle Trigonometry 4 ed. [S.l.]: Thomson Brooks/Cole. ISBN 0-534-40230-5
- Serway, Raymond A.; Jewett Jr., John W. (2005). Principles of Physics. [S.l.]: Brooks/Cole—Thomson Learning. ISBN 0-534-49143-X
- Shankar, Ramamurti (1994). Principles of Quantum Mechanics 2 ed. [S.l.]: Springer. p. 81. ISBN 0-306-44790-8
- Smith, David Eugene (1925). History of Mathematics, Vol II. Boston: Ginn and Co.
- Smith, Julius O. (2003). «Euler's Identity». Mathematics of the Discrete Fourier Transform (DFT). [S.l.]: W3K Publishing. ISBN 0-9745607-0-7. Consultado em 22 de setembro de 2006
- Stewart, Ian; Tall, David (1983). Complex Analysis (the Hitchhiker's Guide to the Plane). [S.l.]: Cambridge University Press. ISBN 0-521-28763-4
- Taylor, John R. (2005). Classical Mechanics. [S.l.]: University Science Books. ISBN 1-891389-22-X
- Torrence, Bruce Follett; Torrence, Eve (1999). The Student's Introduction to Mathematica. [S.l.]: Cambridge University Press. ISBN 0-521-59461-8















![{\displaystyle (-180^{\circ },180^{\circ }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52564e11cb8ecd24997d7929ef3ff9a87052b335)

![{\displaystyle (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fbb1843079a9df3d3bbcce3249bb2599790de9c)








![{\displaystyle \phi \in (-\pi ,\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37a9db276fa2848727409fad003905e9d87e6328)














































































![{\displaystyle L=\int _{a}^{b}{\sqrt {\left[r(\phi )\right]^{2}+\left[{\tfrac {dr(\phi )}{d\phi }}\right]^{2}}}d\phi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/596d00a5b2e764eca7c56d034de7f5a90f2441fb)



![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)










![{\displaystyle J=\det {\frac {\partial (x,y)}{\partial (r,\phi )}}={\begin{vmatrix}{\frac {\partial x}{\partial r}}&{\frac {\partial x}{\partial \phi }}\\[8pt]{\frac {\partial y}{\partial r}}&{\frac {\partial y}{\partial \phi }}\end{vmatrix}}={\begin{vmatrix}\cos \phi &-r\sin(\phi )\\\sin \phi &r\cos(\phi )\end{vmatrix}}=r\cos ^{2}(\phi )+r\sin ^{2}(\phi )=r}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35f71f9a6a360d6c632169e91ab37751ef95f06c)