Condução térmica

No estudo da transferência de calor, condução térmica ou difusão térmica (ou ainda condução ou difusão de calor) é a transferência de energia térmica entre átomos e/ou moléculas vizinhas em uma substância devido a um gradiente de temperatura. Em outras palavras, é um modo do fenômeno de transferência térmica causado por uma diferença de temperatura entre duas regiões em um mesmo meio ou entre dois meios em contato no qual não se percebe movimento global da matéria na escala macroscópica, em oposição à convecção que é outra forma de transferência térmica.[1]
Calor pode ser transferido também por radiação e/ou convecção, e frequentemente mais que um destes processos ocorre simultaneamente em uma dada situação.
Fundamentos[editar | editar código-fonte]
O fluxo de calor sempre ocorre a partir de uma região de maior temperatura para uma região de baixa temperatura, e atua no sentido de equalizar as diferenças de temperatura.[2] Genericamente, a propagação de calor por condução ocorre sem transporte da substância formadora do sistema, ou seja, através de choques entre suas partículas integrantes ou intercâmbios energéticos dos átomos, moléculas, e elétrons. A condução térmica pode ser interpretada como a transmissão passo a passo de agitação térmica: um átomo (ou uma molécula) transfere parte de sua energia cinética ao átomo vizinho, sendo assim um fenômeno de transporte de energia interna provocado pela heterogeneidade da agitação molecular, sendo assim um fenômeno termodinamicamente irreversível.
Condução nos diversos estados da matéria[editar | editar código-fonte]
Condução ocorre em todas as formas de matéria, sólidos, líquidos, gases e plasmas, mas não requer qualquer movimento macroscópico de massa da matéria condutora, mas apenas de seus componentes subatômicos ou sua vibração, em escala microscópica. A condução é o meio mais importante de transferência de calor dentro de um sólido ou objetos sólidos em contato térmico. A condução é maior nos sólidos, porque a rede espacial de relações relativamente fixas entre os átomos contribui para a transferência de energia entre eles por vibração.[3][4][5]
A transferência inter-molecular de energia pode ser primariamente por impacto elástico como em fluidos ou por difusão de elétrons livres como em metais ou vibração de fônons como em isolantes. Em isolantes o fluxo de calor é conduzido quase inteiramente por vibração de fônons.
Em termos mais específicos, em sólidos, se deve à combinação das vibrações das moléculas em um retículo cristalino e ao transporte de energia por elétrons livres.[6] Os elétrons susceptíveis ao movimento denominam-se elétrons de condução no modelo do elétron livre.[7] A condução de calor no interior de um sólido é diretamente análoga a difusão de partículas dentro de um fluido, na situação em que não há correntes do fluido.
Para quantificar a facilidade com a qual um meio particular conduz calor, os engenheiros empregam a condutividade térmica, também conhecida como constante ou coeficiente de condutividade, . Em condutividade térmica é definido como "a quantidade de calor, , transmitida num tempo () através de uma espessura (), em uma direção normal à superfície de área (), devido à diferença de temperatura () [...]." Condutividade térmica é uma "propriedade" do material que é primariamente dependente da fase do meio, temperatura, densidade, e ligação molecular. [3][5][8][9][10]
Efusividade térmica é uma quantidade derivada da condutividade a qual é uma medida da capacidade de um material para trocar energia térmica com suas redondezas. É, essencialmente, a impedância térmica de uma amostra, ou seja, a habilidade que uma amostra tem de trocar calor com o meio ambiente.[11][12]
A densidade diminui a realização da condução. Portanto, os fluidos (e especialmente gases) são menos condutivos. Isto é devido à grande distância entre os átomos de um gás: menos colisões entre átomos significa menos condução. A condutividade dos gases aumenta com a temperatura. A condutividade aumenta com a crescente pressão de vácuo até um ponto crítico que a densidade do gás é de tal forma que as moléculas do gás pode ser previstas como colidindo umas com as outros antes de transferir o calor de uma superfície para outra. Após este ponto a condutividade aumenta ligeiramente com a crescente pressão e densidade.
Condutância térmica de contato é o estudo da condução de calor entre corpos sólidos em contato. Uma queda de temperatura é frequentemente observada uma interface entre as duas superfícies em contato. Este fenômeno é dito ser o resultado de uma resistência térmica de contato existente entre as superfícies em contato. Resistência térmica interfacial é uma medida de uma resistência de uma interface ao fluxo térmico. Esta resistência térmica difere da resistência de contato, já que ela existe mesmo em interfaces atomicamente perfeitas, nas quais cada átomo de uma superfície esteja em posição no retículo cristalino dos sólidos, sem interstícios ou soluções de continuidade, defeitos na sua malha de átomos. Compreender a resistência térmica na interface entre dois materiais é de importância primordial no estudo de suas propriedades térmicas. Interfaces muitas vezes contribuem de forma significativa para as propriedades observadas dos materiais.
Em termos mais estatísticos, em fluidos (líquidos e gases), o transporte de energia é resultante da não-uniformidade do número de choques por unidade de volume, durante seu movimento aleatório, semelhante ao fenômeno da difusão molecular[1]pg 158. Em sólidos, a condução de calor é fornecida conjuntamente por condução de elétrons e vibração da rede cristalina (fônon)[1]pg 160.
Os metais (e.g. cobre, platina, ouro, etc.) e suas ligas (e.g. latão, bronze, aço, etc.), sejam sólidos ou líquidos (como em temperatura ambiente o mercúrio (elemento)), devido às suas elevadas condutividades térmicas, são excelentes meios de propagação de calor, e são normalmente os melhores condutores de energia térmica, pela sua relação com o movimento de elétrons livres, que normalmente está associada à condutividade elétrica.[13]
Isto é devido ao meio pelo qual os metais são quimicamente ligados: ligações metálicas (como opostas a ligações covalentes ou iônicas) tem elétrons de livre movimentação os quais são capazes de transmitir energia térmica rapidamente através do metal. O "fluido elétrico" de um sólido metálico condutivo conduz facilmente todo o fluxo de calor através do sólido. Fluxo de fônons está ainda presente, mas carrega menos que 1% da energia. Elétrons também conduzem corrente elétrica através de sólidos condutivos, e as condutividades térmica e elétrica da maioria dos metais tem aproximadamente a mesma razão. Um bom condutor elétrico, tal como a prata ou o cobre (os metais de mais alta condutividade elétrica), normalmente também conduz bem calor. O efeito Peltier-Seebeck exibe a propensão dos elétrons em conduzir calor através de um sólido eletricamente condutivo. A termoeletricidade é causada pela relação entre elétrons, fluxos de calor e correntes elétricas.[14]
Os gases e alguns sólidos, que possuem baixa condutividade térmica, são considerados péssimos meios de propagação de calor, sendo definidos como isolantes térmicos, e assim aplicados, como se vê em materiais que causam isolamento pelo aprisionamento de gases ou líquidos, em grandes taxas, como o poliestireno expandido ou a lã de vidro
Condução em estado estacionário[editar | editar código-fonte]
Condução em estado estacionário é a forma de condução que ocorre quando a diferença de temperatura conduzindo a condução é constante de modo que após um tempo de equilíbrio, a distribuição espacial das temperaturas (campo de temperatura) no objeto condutor não mais se altera. Assim, todas as derivadas parciais de temperatura com relação ao espaço tem valores, mas todos as derivadas da temperatura em função do tempo são uniformemente nulas (possuem valor igual a zero). Por exemplo, uma barra pode ser fria em uma extremidade e quente na outra, mas depois que um estado de condução em estado estacionário é atingido, o gradiente espacial de temperatura ao longo da barra não mais altera-se com o tempo. Em vez disso, a temperatura em qualquer ponto dado da haste permanece constante, e essa temperatura varia linearmente no espaço, ao longo da direção de transferência de calor.
Na condução em estado estacionário, a quantidade de calor que entra uma seção é igual à quantidade de calor que sai. Na condução em estado estacionário, todas as leis de condução de corrente elétrica direta (ou contínua) podem ser aplicadas a similares "correntes de calor". Em tais casos, é possível tomar "resistências térmicas", como o analógico para resistências elétricas. A temperatura desempenha o papel de tensão e de calor transferido é o analógico da corrente elétrica.
Condução transiente[editar | editar código-fonte]
Existem também situações de estado não estacionário, nas quais uma alteração de temperatura ou fonte de calor pode ser repentinamente introduzida, e a condução de calor no interior de um objeto não tem tempo de se ajustar ao novo fluxo de calor. Em tais situações, os fluxos de calor e as temperaturas no interior dos objetos mudam com o tempo, até um novo estado estacionário de gradiente térmico, ou então um estado de temperatura uniforme é alcançado (o que sempre acontece, eventualmente, se as temperaturas externas e as fontes de calor e seus sumidouros não são alterados). Durante o período de tempo que a temperatura em qualquer ponto do espaço em um objeto ou uma mudança de fluidos no tempo, o modo de condução de calor é chamado de condução transiente. A palavra transiente refere-se a distribuições de temperatura no interior do objeto, que mudam ao longo do tempo e, portanto, são transitórias.
A condução transiente ocorre (por um tempo) em qualquer situação onde há uma alteração na temperatura das fontes externas ou internas ou dissipadores de calor, causando uma nova fonte de entrada de calor (ou saída) no interior de um objeto, ou dentro ou fora do objeto (para as proximidades). Novas fontes de calor "ativadas" no interior de um objeto podem causar o fenômeno (por exemplo, na partida de um motor em um carro). Novas condições externas também causam esse processo: a barra de cobre no exemplo acima seria uma experiência de condução transiente pois uma extremidade estava submetida a uma temperatura diferente da outra. Ao longo do tempo, o campo de temperaturas no interior do bar chegaria a um novo estado de equilíbrio (um estado estacionário), no qual um gradiente de temperatura constante ao longo do barra vai finalmente ser criado, e este gradiente então permaneceria constante, no tempo. Normalmente, esse novo gradiente de estado estacionário é atingida exponencialmente com o tempo, depois que uma fonte de temperatura ou calor novo ou dissipação for introduzido. Nesta medida, a fase de "condução transiente" é, então, dominante, embora o fluxo de calor pode ser ainda continuar em alta potência. Por exemplo, em um automóvel, a fase transitória de condução térmica seria inicialmente predominante, e a fase de estado estacionário aparece, logo que o motor tenha atingido o estado estacionário, a temperatura operacional.
Um exemplo de condução transiente mas a que não finaliza-se com uma condução em estado estacionário, mas não dominada pela transferência de calor por condução mas por convecção, ocorreria quando uma bola de cobre quente cai em óleo em baixa temperatura. Aqui o campo de temperatura dentro do objeto começa a mudar em função do tempo, à medida que o calor é removido do metal, o interesse reside em analisar essa mudança espacial da temperatura dentro do objeto ao longo do tempo, até desaparecerem por completo todos os gradientes (a bola alcança a mesma temperatura que o óleo). Matematicamente, esta condição é também atingida exponencialmente; em teoria ela tomaria tempo infinito, mas na prática é mais, para todos os efeitos, em um período muito curto. Ao final deste processo sem dissipador de calor, mas as partes internas da bola (as quais são finitas), não existe estado estacionário se condução de calor a ser alcançado. Tal estado nunca ocorre nesta situação, mas sim o fim do processo é quando não há condução de calor na totalidade.
A análise de sistemas de condução de estado não estacionário é mais complexa que sistemas de estado estacionário, e (exceto para formas simples) pede a aplicação das teorias de aproximação e/ou análise numérica por computador. Um método gráfico popular envolve o uso de cartas de Heisler.
Condução relativística[editar | editar código-fonte]
A teoria da condução de calor relativística é um modelo que é compatível com a teoria da relatividade especial. Na maior parte do século passado, foi reconhecido que a equação de Fourier está em contradição com a teoria da relatividade porque admite uma velocidade infinita de propagação de sinais de calor. Por exemplo, segundo a equação de Fourier, um pulso de calor na origem seria sentido no infinito instantaneamente. A velocidade de propagação de informações seria mais rápida que a velocidade da luz no vácuo, o que é fisicamente inadmissível no âmbito da relatividade. Alterações ao modelo de Fourier prevendo um modelo relativista de condução de calor, evitam esse problema.
Condução quântica[editar | editar código-fonte]
Segundo som é um fenômeno mecânico quântico no qual transferência de calor ocorre por movimento na forma de onda, em vez de pelo mecanismo mais comum da difusão. Calor toma o lugar da pressão nas ondas de som normais. Isto conduz a uma condutividade térmica muita alta. É conhecido como "segundo som" porque a onda de calor é similar à propagação de som no ar.
Lei de Fourier[editar | editar código-fonte]
A lei da condução térmica, também conhecida como lei de Fourier, estabelece que o fluxo de calor através de um material é proporcional ao gradiente negativo de temperatura. Podemos enunciar esta lei de duas formas equivalentes: a forma integral, em que olhamos para a quantidade de energia que flui para dentro ou para fora de um corpo como um todo; e a forma diferencial, em que olhamos para os fluxos de energia localmente. O fluxo de calor é a quantidade de energia que flui através de uma unidade de área por unidade de tempo.
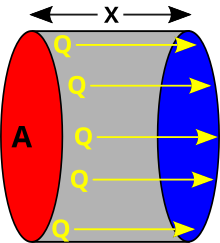
Pode-se determinar o fluxo de calor transportado por condução pela Lei de Fourier:
A expressão acima aplica-se ao caso unidimensional, quando há gradiente de temperatura apenas na direção .
Se a distribuição de temperatura for linear e, neste caso , a equação acima toma a forma:
A constante , é a condutividade térmica do material. Entre duas substâncias, a que tiver condutividade maior conseguirá transferir uma quantidade maior de calor, para uma mesma diferença de temperatura.
Teorização completa[editar | editar código-fonte]

Existem várias grandezas envolvidas, mas entre elas existem duas que são de muita importância de interesse prático no estudo de problemas de condução de calor. Estas grandezas são a razão de fluxo de calor e a distribuição da temperatura. As razões de fluxo de calor tratam da demanda de energia em um dado sistema, quando se requer uma distribuição de temperaturas conveniente para desenhar de maneira adequada no sistema, desde o ponto de vista dos materiais. Em um fenômeno qualquer, uma vez que seja conhecida a distribuição da temperatura é possível determinar as razões de fluxo de calor com ajuda da denominada Lei de Fourier (de 1822, estabelecida por Jean Baptiste Joseph Fourier).
A distribuição da temperatura é linear, e o fluxo de calor é constante de um extremo a outro de uma placa, para o caso da equação radial produzida.
E portanto a distribuição da temperatura apresenta-se em forma logarítmica:
O calor transferido é tratado pela lei de Fourier que descreve especificamente previsões (modelagens) de comportamento para o caso simples de um corpo sólido, com duas paredes paralelas:[15][16]
A unidade de é o Watt (), e sendo as grandezas:
- a temperatura da superfície da parede mais quente
- a temperatura da superfície da parede fria
- da área através da qual o calor flui,
- a condutividade térmica, geralmente um parâmetro do material dependente da temperatura, e
- a espessura do corpo, medido de parede a parede.
Atualmente a transferência de calor é descrita através do conceito mais rigoroso de fluxo de calor , em abordagens que visam reduzir-se aos tratamentos de Fourier e Newton. A notação é formulada a partir da derivada parcial no tempo do vetor fluxo de calor . Aplica-se a seguinte definição:
Matematicamente, o fenômeno de "transferência de calor" é descrito por uma equação diferencial parcial, apresentando um padrão parabólico. Esta equação diferencial parcial, na forma especificada, apresenta a forma geral:
Sendo esta equação especial e chamada comumente equação do calor. Note-se que esta forma da equação do calor é válida somente para meios homogêneos e isotrópicos; noutras palavras, para meios que possuem a mesma composição em todos os lugares e nenhuma orientação preferencial (ocorrem orientações preferenciais, por exemplo, em fibras de materiais compostos, mas também por dilatações de grãos em chapas de aço laminadas, etc). Para estes casos - e apenas para isso , as propriedades materiais são adotadas com o objetivo de considerar apenas as grandezas dependentes da temperatura. Estritamente falando, a equação assim formulada não se aplica apenas quando o calor no corpo é introduzido ou removido por fenômenos estranhos à modelagem utilizada, sendo, neste caso, a fonte ou "fuga" um termo a ser adicionado ao equacionamento. Com estas restrições, segue-se a seguinte forma da equação do calor:
Sendo esta a equação diferencial que descreve os processos de transporte em geral (como o processo de difusão - que é um transporte material, devido a ser compreendido como uma diferença de concentração ou, no caso da equação do calor, apenas o "andar" da distribuição de temperatura em um corpo devido a um gradiente de temperatura). A solução analítica dessa equação não é em possível muitos casos práticos, sendo calculados, atualmente, com a ajuda de métodos tecnicamente relevantes de cálculos para fenômenos de transferência de calor como o método dos elementos finitos, obtendo-se como resultado a distribuição temporal da temperatura no espaço (um campo de temperaturas). Assim, pode-se obter influências, por exemplo, relacionadas ao comportamento de expansão espacial dos componentes (dilatação térmica), que por sua vez influenciará o estado de tensão local. Assim, o campo de temperaturas torna-se uma base importante para todas as tarefas de engenharia em que o componente de estresse térmico não pode ser negligenciado no projeto.
Forma diferencial[editar | editar código-fonte]
A forma diferencial da lei de Fourier da condução térmica mostra que o fluxo de calor local, , é igual ao produto da condutividade térmica, , e o gradiente de temperatura local negativo, . O fluxo de calor é a quantidade de energia que flui através de uma superfície particular por unidade de área por unidade de tempo.
onde (incluindo as unidades SI)
- é o fluxo de calor local, [W·m−2]
- é a condutividade térmica do material, [W·m−1·K−1],
- é o gradiente de temperatura, [K·m−1].
A condutividade térmica, , é frequentemente tratada como um constante, embora isto nem sempre seja verdade. Enquanto a condutividade térmica de um material geralmente varia com a temperatura, a variação pode ser pequena para uma significativa faixa de temperaturas para alguns materiais comuns. Em materiais anisotrópicos, a condutividade térmica varia tipicamente com orientação; neste caso é representada por um tensor de segunda ordem. Em materiais não uniformes, varia com a localização espacial.
Para muitas aplicações simples, a lei de Fourier é usada em sua forma unidimensional. Na direção ,
Forma integral[editar | editar código-fonte]
Pela integração da forma diferencial sobre a superfície total do material , chega-se à forma integral da lei de Fourier:
onde (incluindo as unidades SI)
- é a quantidade de calor transferido por unidade de tempo e
- é um elemento de área de superfície orientado
A equação diferencial acima, quando integrada para um material homogêneo de geometria 1-D entre dois pontos a uma temperatura constante, dá a taxa de fluxo de calor como:
onde
- é a área da superfície da seção transversal,
- é a diferença de temperatura entre os extremos,
- é a distância entre os extremos.
Esta lei forma a base para a derivação da equação do calor. A lei de Ohm é o análogo elétrico da lei de Fourier.
Condutância[editar | editar código-fonte]
Escrevendo-se
onde é a condutância, em .
Lei de Fourier pode também ser enunciada como:
A recíproca da condutância é a resistência, , dada por:
e é a resistência que é aditiva quando várias camadas condutivas situam-se entre as regiões quente e fria, porque e são as mesmas para todas as camadas. Em uma partição de multicamadas, a condutância total está relacionada com a condutância de suas camadas por:
Assim, quando trata-se de uma partição de multicamadas, a seguinte fórmula é geralmente usada:
Quando o calor é conduzido a partir de um fluido para outro através de uma barreira, às vezes é importante considerar a condutância da fina película de fluido que permanece estacionária próximo a barreira. Esta fina película de líquido é difícil de quantificar, suas características, dependendo das complexas de turbulência e viscosidade, mas quando se lida com os obstáculos finos de alta condutância por vezes pode ser bastante significativa.
Representação de propriedade intensiva[editar | editar código-fonte]
As equações de condutância anteriores escritas em termos de propriedades extensivas, podem ser reformuladas em termos de propriedades intensivas. Idealmente, as fórmulas de condutância devem produzir uma grandeza com dimensões independentes da distância, como a lei de Ohm da resistência elétrica:
- ,
e a condutância:
- .
A partir da fórmula elétrica:
- ,
onde é a resistividade, é o comprimento e é a área de seção tranversal, temos
- ,
onde é a condutância, é a condutividade, é o comprimento e é a área de seção tranversal.
Para o calor,
onde é a condutância.
Lei de Fourier pode ser enunciada como:
análoga a lei de Ohm:
- ou
A recíproca da condutância é resistência, , dado por:
análoga a lei de Ohm:
A soma das condutâncias em série é ainda correta.
Cilindros[editar | editar código-fonte]
Condução através de cilindros pode ser calculada quando conhece-se variáveis tais como o raio interno , o raio externo , e o comprimento notado como .
A diferença de temperatura entre a parede interna e externa pode ser expressa como .
A área do fluxo de calor:
Quando a equação de Fourier é aplicada:
Rearranjando-se:
Portanto, a taxa de transferência de calor é
A resistência térmica é
Tendo-se , onde sendo importante notar que este é o raio log médio.
Condução em regime estacionário[editar | editar código-fonte]
Define-se um regime estacionário (ou permanente), quando as temperaturas não dependem do tempo. A temperatura depende apenas da disposição do ponto em que as medidas são tomadas ao longo do tempo. Para o restante desta divisão deste artigo, assume-se como estabelecido um estado de equilíbrio.
Superfície plana simples[editar | editar código-fonte]
O material é um meio condutor térmico delimitado por dois planos paralelos (o caso de uma parede). Cada plano tem uma temperatura homogênea por toda a sua superfície. Consideramos que os planos têm duas dimensões infinitas para superar os efeitos de borda. Por conseguinte, o fluxo de entrada é igual ao de saída, não há perda de calor nas extremidades.
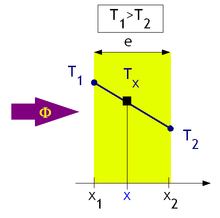
Note-se que a temperatura do plano situado na abscissa , e a temperatura do plano situado na abscissa . Note-se que é a espessura da parede. Em regime estacionário, é uma função linear de , assim:
A densidade de fluxo de calor da superfície é escrita como:
- .
O fluxo de calor através de uma superfície é:
ou

Analogia elétrica
Por analogia com a eletricidade (lei de Ohm) no caso especial onde a área de contato entre cada material é constante (fluxo superficial constante), podemos traçar um paralelo entre as duas expressões:
Pode-se traçar um paralelo da primeira com a tensão e a temperatura, da outra parte a intensidade e o fluxo de calor:
Pode-se então definir uma resistência térmica, desempenhando a transferência de calor um papel semelhante ao da resistência elétrica.
onde é a superfície do material e a espessura. A resistência térmica é homogênea e expressa em .
Surperfícies planas em série[editar | editar código-fonte]
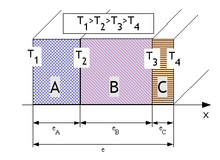
Considere-se materiais A,B e C de espessura respectivamente , e e de condutividade térmica respetivamente , e .
Os pressupostos são idênticos aos de uma única superfície plana. Consideramos que o contacto entre cada camada é perfeito, o que significa que a temperatura na interface entre dois materiais é idêntica em cada material (temperatura não salta na passagem por uma interface).
Finalmente, a área de contato entre cada material é constante, o que implica um fluxo de superfície constante.
As resistências térmicas se adicionam:
Demonstração[editar | editar código-fonte]
Globalmente, tem-se
Se decomposto
- para a camada :
- para a camada :
- para a camada :
Nota: Dadas as hipóteses, o fluxo (ou a densidade de fluxo) permanece constante.
Com:
Portanto
O perfil de temperaturas
Para cada material a variação da temperatura segue uma lei do tipo:
A variação de temperatura é linear na espessura do material considerado. A inclinação é inversamente proporcional a (condutividade térmica) característica de cada material. Quanto maior a condutividade térmica e menor o material (e, portanto, menor o isolamento), menor será a inclinação.

Analogia elétrica
Da mesma forma que as resistências elétricas em série são adicionadas, as resistências térmicas em série são somadas.

Superfícies planas em paralelo[editar | editar código-fonte]

Considere-se materiais planos justapostos lado a lado. Cada material é homogêneo e delimitado por dois planos paralelos. Este poderia ser o modelo de uma parede com uma janela. As hipóteses são idênticas as de uma superfície plana única. Além disso, considera-se que a temperatura da superfície é uniforme em cada elemento ( et ). Considere-se as respectivas superfícies dos elementos .
Posteriormente, presume-se que o fluxo seja sempre perpendicular à parede composta; o que não é realista porque a temperatura da superfície de cada elemento da composição é diferente e há, portanto, um gradiente de temperatura lateral (a origem das pontes térmicas). Além disso, é necessário corrigir o fluxo de calor calculado na parede feita com os coeficientes de perda por unidade de comprimento, específicos para cada ramo de parede (e pode ser insignificante, cf. a regulamentação térmica RT 2000[17]).
As condutâncias térmicas se adicionam:
Demonstração[editar | editar código-fonte]
Para cada elemento , o fluxo é expresso em função da relação
Tendo-se em conta a analogia elétrica
como é igual a , ou
Tem-se, portanto
O fluxo total é igual à soma dos fluxos em cada elemento
Sendo a surperfície total
O fluxo na superfície é então
Mais uma vez, por analogia com as leis elétricas, o inverso da resistência térmica é às vezes chamado condutividade térmica.
Analogia elétrica
Também é possível fazer uma analogia entre um circuito elétrico de resistências em paralelo.
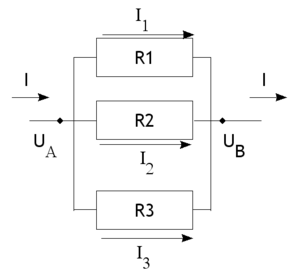 |
 |
Superfície cilíndrica simples[editar | editar código-fonte]

O tubo simples consiste de um material único e homogêneo. A temperatura é uniforme em cada superfície do tubo. Considera-se o tubo infinitamente longo para superar os efeitos da borda.
A variação de temperatura é escrito:
Demonstração[editar | editar código-fonte]
Considera-se uma variação dentro do material constituinte do tubo, a lei de Fourier é então expressa como:
Variação da temperatura na espessura do tubo

Sendo a superfície de um cilindro:
Podemos escrever a lei de Fourier na forma:
A variação de temperatura no material é
Em toda a espessura do tubo, a variação é
Superfícies cilíndricas concêntricas[editar | editar código-fonte]

O tubo concêntrico é composto por tubos dispostos em camadas concêntricas. Considere-se que o contato é perfeito entre os tubos. A temperatura é uniforme em cada superfície do tubo. Considere-se que o tubo possui um comprimento interminável L para superar os efeitos de borda.
A resistência total do tubo é expressa por uma lei da tipo "série como a parede compondo uma série:
Demonstração[editar | editar código-fonte]
Evolução da temperatura na primeira camada:
Evolução da temperatura na segunda camada:
Em toda a espessura do tubo:
A resistência térmica da camada
A resistência térmica da camada
Chegando-se a que resistência total do tubo é expressa por uma lei da tipo "série como a parede compondo uma série:
Condução em regime dinâmico[editar | editar código-fonte]
A resolução da equação do calor em regime dinâmico é muito mais difícil. Ela usa os conceitos de transformada de Fourier de produto de convolução e distribuições. Apresentam-se alguns exemplos de resolução.
Caso de uma área ilimitado[editar | editar código-fonte]
Princípio geral[editar | editar código-fonte]
Escreve-se a equação do calor na forma:
onde é o coeficiente de difusividade térmica e representa as fontes de calor. pode ser uma função do tempo e da posição da fonte de calor, mas também uma distribuição. Por exemplo, a injeção instantânea e pontual de uma quantidade de calor pode ser representada pelo produto de uma distribuição de Dirac no instante por uma distribuição de Dirac em é a abscissa em caso de problema unidimensional ou vetor de posição no caso geral.
Ela também dará o estado inicial do área , que também pode ser uma função de ou uma distribuição. Considera-se que é nulo para .
O método de solução consiste em:[18] [19]
- Aplica-se uma transformada de Fourier sobre a variável , a todos os termos da equação diferencial. Isto transforma a derivação com relação a em um produto. Toma-se , então a equação torna-se:
ou melhor, no sentido de distribuições:
tendo-se em conta a condição inicial.
- Reconhecendo-se nesta equação um produto de convolução:
O operador aplicado a é um produto de convolução relativo à variável .
- Aplicando o operador inverso, prova-se que , onde é a função de Heaviside, conduzindo a:
Se é uma função e não uma distribuição, esta relação se torna, para :
- Toma-se a transformada de Fourier inversa para deduzir .
Caso particular[editar | editar código-fonte]

Toma-se em (injeção instantânea de calor em um determinado ponto), o método acima descrito conduz a:
Assim, para :
cuja transformada de Fourier inversa é, para :
- no caso unidimensional.
- no caso tridimensional.
Área ilimitado sem fonte de calor[editar | editar código-fonte]
Se toma-se somente a temperatura inicial de uma fonte média independente de calor (), tem-se que:
- no caso unidimensional.
- no caso tridimensional.
Caso de áreas limitadas, sem fonte de calor[editar | editar código-fonte]
Caso de uma área limitada por um plano. O problema de Kelvin[editar | editar código-fonte]

Supondo-se o área limitada pelo plano . Se coloca-se por condição os limites suplementares para todo , então basta estender a distribuição inicial de temperatura por uma função ímpar em e aplicar-se o resultado anterior.
O caso mais célebre é o problema de Kelvin. Este considerou em 1860 que a Terra estava inicialmente a uma temperatura constante da ordem de 3000° e que se resfriava por simples condução. Utilizando o valor atual do gradiente de temperatura em função da profundidade, ele deduziu uma estimativa para a idade da Terra. Pode-se aplicar o método de resolução acima para considerar a Terra como plana e infinitamente profunda, delimitado por um plano de sua superfície. O cálculo conduz a:
onde é chamada função erro de Gauss.
O gradiente de temperatura na superfície será:
Conhecendo-se como sendo da ordem de 3 °C para cada 100 metros de profundidade e estimado como , obtem-se que t vale 100 milhões de anos. Este resultado é largamente subestimado pois Kelvin ignora os fenômenos de convecção no interior do manto terrestre.[20] [21]
Caso de uma área limitada por dois planos paralelos[editar | editar código-fonte]

Considere-se uma área limitada por dois planos e . Supondo-se que são dadas como condições de contorno os limites . Utiliza-se um método de resolução baseado nas séries de Fourier, procurando-se sob a forma:
Esta expressão verifica tanto a equação do calor quanto as condições de contorno nos limites. Se é tomada a distribuição de temperatura inicial , é suficiente expandir-se em uma série de Fourier para determinar-se os coeficientes .
Por exemplo, se tiver-se constante, obtem-se:
Ao deixar-se L ao infinito, encontra-se a solução de Kelvin do parágrafo anterior, a soma acima é considerado uma soma de Riemann convergindo para a integral.
Caso de uma área de geometria esférica[editar | editar código-fonte]

Se o caso de propagação se sá em uma área esférica, e onde a temperatura não depede apenas das distância ao centro, a equação de calor torna-se a expressão do laplaciano em uma esfera:
Se coloca-se , a equação torna-se:
Podemos, então, aplicar os métodos anteriores para determinar , então deduzir dividindo por .
Assim, resolvendo-se o problema de Kelvin, no caso de uma esfera de raio (temperatura inicial uniforme igual à ,a superfície é mantida a uma temperatura igual a zero) conduz à seguinte expressão para :
onde é a função sinus cardinal.
Caso de áreas limitadas, com fonte de calor[editar | editar código-fonte]
Considere-se a equação:
com não nulo. Em geral, procura-se uma solução particular para esta equação, de modo que, uma vez relacionada a , pode ser reduzida a uma equação sem segundo membro. Apresentam-se alguns exemplos, onde representa uma densidade de fonte de calor constante, independente da posição e do tempo.
Área limitada por dois planos paralelos[editar | editar código-fonte]

Considere-se uma área limitada pelos dois planos e . Supondo-se que no momento inicial, a temperatura da área é igual a uma temperaturea de referência nula, e que as bordas da área se manterão permanentemente esta temperatura nula. satisfaz, pois:
- para todo positivo.
- para todo entre e .
A função independente de satisfaz as duas primeiras relações, de maneira que coloca-se que , então satisfaz:
Pode-se aplicar o método visto acima na busca de sob a forma de uma série:
que satisfaça as duas primeiras relações. Dado que, por razões de simetria, é esperado que , pode-se supor que os coeficientes sejam nulos quando é par, de maneira que:
Para , tem-se:
Obtem-se em desenvolver-se em série de Fourier. Encontrando-se:
Assim , finalmente:
Quando tende ao infinito, a temperatura da área tende a , o aquecimento tende a se equilibrar com a perda de calor pelas duas bordas.
Área limitada por um plano[editar | editar código-fonte]

A resolução do mesmo problema do caso em que consiste em determinar tal que:
- para todo positivo.
- para todo .
Pode ser obter a solução deixando infinito na expressão dada no parágrafo anterior, igualando a série a uma soma de Riemann. Isto resulta na seguinte expressão:
é a função chamada função erro de Gauss. Pode-se também encontrar esta expressão pela aplicação do método derivado do princípio geral relativo a uma área ilimitada, depois de estender a todo o espaço as funções em duas funções ímpares em , de modo que se anula em .
Quando tende ao infinito, é de cerca de , análogo aquela de uma área infinita. A borda única não é suficiente para dissipar o calor.
Área de uma geometria esférica[editar | editar código-fonte]

Dado o caso de uma área cuja borda seja uma esfera de raio , utiliza-se a expressão do Laplaciano em esfera e tem-se de resolver:
- Para todo
- Para todo
Pergunta-se se , satisfaz o sistema:
- Para todo
- Para todo
O método das séries de Fourier sugere a busca de sob a forma de uma série , onde os coeficientes encontram-se em desenvolvimento em série de Fourier. Obtendo-se:
e, portanto:
onde é a função sinus cardinal.
Quando tende ao infinito, a temperatura tende à distribuição limite .
Ver também[editar | editar código-fonte]
- Calor
- Condutividade térmica
- Fluxo de calor
- Tranferência de calor
- Valor U de isolamento
- Tubulação de calor
- Lei de Fick da difusão
- Condução de calor relativística
- Equação de Churchill-Bernstein
- Condução elétrica
- Condutância elétrica
Referências
- ↑ a b c J.Ph. Pérez et A.M. Romulus. Thermodynamique. Fondements et applications, Masson, Paris, 1993. ISBN 2-225-84265-5 pg 153
- ↑ YOUNG, H.D; FREEDMAN, R.A (2008). Física II: Termodinâmica e Ondas 12 ed. São Paulo: Addison-Wesley. p. 190. ISBN 978-85-88639-33-1
- ↑ a b Halliday, D., Resnick, R., Walker, J., Fundamentos de Física 2 - São Paulo: Livros Técnicos e Científicos Editora, 4a Edição, 1996. ISBN 978-852-161-904-8
- ↑ Nussenzveig, H. M. – Física Básica – 2ª ed. - vol. 2 - seção 7.1 – Ed. Edgard Blücher Ltda - 1981. ISBN 978-852-120-163-2
- ↑ a b Sears, F. W. E Zemansky, M. W. – Física - vol. 2, cap. 15, Ed. Universidade de Brasília, Rio de Janeiro – 1973.
- ↑ ASHCROFT, N. W & MERMIN, N. D. Solid State Physics. l.ed. New York: Holt, Rinehart and Winstone, 1976. 826p.
ASHCROFT, N. W & MERMIN, N. D. Solid State Physics. l.ed. Cengage Learning, 2011, ISBN 8-131-50052-7 - ↑ Carlos Ariel Samundio Pérez;O MODELO DO ELÉTRON LIVRE DE DRUDE COMPLETA 100 ANOS - www.periodicos.ufsc.br
- ↑ Kim S., Kim M. C., Kim K. Y., 2003, “Estimation of Temperature-Dependent Thermal Conductivity With a Simple Integral Aproach”, Int. Comm. Heat Transfer, vol. 30, nº 4, p. 485-494.
- ↑ Lesnic D, et all, 1995,A Note on The Determination of Thermal Properties a Material in a Transient Nonlinear Heat Conduction Problem Department of Applied Mathematical Studies, University of Lees, Int.Comm.Heat Mass Transfer, Vol.22, No.4, pp.475-482.
- ↑ Touloukian, Y. S., Powell, R. W., Ho, C. Y. and Klemens, P. G., 1970, Thermophysical Properties of Matter - Volume 2, Thermal Conductivity: Nonmetallic Solids, IFI/Plenum, New York, 933 p. ISBN 0-306-67022-4
- ↑ Incropera, F. e De Witt, D., Fundamentos de Transferência de Calor e de Massa. Editora Guanabara Koogan, 3a Edição, 1992. ISBN 0-471-87497-3
- ↑ BEIN, B. K.; PELZL, J. Analysis of surfaces exposed to plasmas by nondestructive photoacoustic and photothermal techniques. Plasma Diagnostics., n. 6, p. 211-326, 1976.
- ↑ DRUDE, P. Zur electronen theorie der matalle. Annalen der Physik, v.1, p. 566, 1900; v.3, p.369, 1900
- ↑ E.R.G. Eckert e R.M. Drake, Analysis of Heat Mass Transfer, McGraw-Hill, New York, 1972.
E.R.G. Eckert e R.M. Drake, Analysis of Heat Mass Transfer, CRC Press; 1986. ISBN 0-891-16553-3 - ↑ Fricke, Jochen; Borst, Walter L.: Energie, Ein Lehrbuch der Physikalischen Grundlagen Oldenbourg Verlag München Wien 1984.
- ↑ Kittel, Charles: Einführung in die Festkörperphysik verschiedene Auflagen, Oldenbourg, München
Kittel, Charles: Einführung in die Festkörperhysik. Mit 519 Bildern, 59 Tabellen. ISBN 978-348-632-763-2 - ↑ RT 2000 Arquivado em 7 de março de 2010, no Wayback Machine.; Collection Recherche Developpement Metier, Novembre 2005 - www.scmf.com.fr
- ↑ L. Landau, E. Lifchitz, Physique théorique, mécanique des fluides, Mir-Ellipses, (1994)
- ↑ Laurent Schwartz, Méthodes mathématiques pour les sciences physiques, Hermann, (1965) ISBN 2-705-65213-2
- ↑ Uma segunda fonte de erros, mais marginal, provém do fato de que Kelvin também negligencia o termo fonte de energia devido à radioatividade. Ver: Voir England P, Molnar P, Richter F, Kelvin, Perry et l'âge de la terre, Pour la Science, février 2008, p.32-37, traduzido para o francês de artigo da American Scientist Arquivado em 6 de setembro de 2013, no Wayback Machine.
- ↑ Jean-Louis Le Mouël, Le refroidissement de la Terre, 196ème conférence de l’Université de tous les savoirs, 14 juillet 2000, [1][ligação inativa] ou [2][ligação inativa]
Bibliografia[editar | editar código-fonte]
- John H Lienhard IV and John H Lienhard V, A Heat Transfer Textbook, Third Edition, Phlogyston Press, Cambridge Massachusetts ISBN 0-971-38352-9 [3]
- Dehghani, F 2007, CHNG2801 – Conservation and Transport Processes: Course Notes, University of Sydney, Sydney
- Çengel, Yunus A.; Heat Transfer - A Practical Approach, McGraw Hill, 2002. ISBN 0-07-011505-2
- Holman, J.P.; Heat Transfer, McGraw-Hill, 1998. ISBN 0-07-114320-3
Ligações externas[editar | editar código-fonte]
- Newton's Law of Cooling (lei do resfriamento de Newton) por Jeff Bryant baseado em um programa por Stephen Wolfram, Wolfram Demonstrations Project. (em inglês)
- When Will My Turkey Be Done? [nota 1]
Notas
- ↑ (Quando estará pronto meu peru ? ) é um exemplo de equações de condução de calor similares aplicadas à lei do resfriamento de Newton a qual prevê o tempo de cozimento de perus e outros assados..

































![{\displaystyle [W]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53adac4d38fc744470f0d0f79113e1c05d9e8564)

![{\displaystyle [m^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69984844e55299dd28db0ef5e3478d6395f4514e)
























































































































































































