Juro
Juro é a remuneração cobrada pelo empréstimo de dinheiro (ou outro item). É expresso como um percentual sobre o valor emprestado (taxa de juro) e pode ser calculado de duas formas: juros simples ou juros compostos.
O juro pode ser compreendido como uma espécie de "aluguel" de dinheiro. A taxa é uma compensação paga pelo tomador do empréstimo para ter o direito de usar o dinheiro até o dia do pagamento. O credor, por outro lado, recebe uma compensação por não poder usar esse dinheiro até o dia do pagamento e por correr o risco de não receber o dinheiro de volta (risco de inadimplência).
História[editar | editar código-fonte]
Documentos históricos redigidos pela civilização suméria, por volta de 3000 a.C., revelam que o mundo antigo desenvolveu um sistema formalizado de crédito baseado em dois principais produtos, o grão e a prata. Antes de existirem as moedas, o empréstimo de metal era feito baseado em seu peso. Arqueólogos descobriram pedaços de metais que foram usados no comércio nas civilizações de Troia, Babilônia, Egito e Pérsia. Antes do empréstimo em dinheiro ser desenvolvido, o empréstimo de cereal e de prata facilitava a dinâmica do comércio.
Na República Romana, no ano do consulado de Marco Fábio Ambusto (pela terceira vez) e ou Tito Quíncio ou Marco Popílio,[1][Nota 1] a taxa de juros foi reduzida para 8 1/3 por cento, mesmo assim, os plebeus continuavam sem conseguir pagar suas dívidas.[2]
Taxa básica de juros[editar | editar código-fonte]
A taxa básica de juros de um país corresponde à remuneração que o tesouro nacional paga aos seus credores, funcionando como taxa de referência para todos os contratos de crédito dessa economia.
No Brasil, a taxa de juros básica é a taxa Selic, que é calculada como a "taxa média ajustada dos financiamentos diários apurados no Sistema Especial de Liquidação e de Custódia (Selic) para títulos federais".[3] Como ferramenta de política monetária, o governo brasileiro interfere na taxa de juros da economia através do Comitê de Política Monetária (COPOM), que tem o papel de definir a meta da taxa Selic[Nota 2] com o objetivo de manter a inflação dentro da meta estabelecida pelo Conselho Monetário Nacional (CMN).[4]
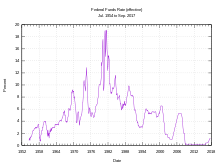
De forma análoga, nos Estados Unidos, a taxa básica de juros é fixada pelo Federal Open Market Committee (Comitê Federal de Mercado Aberto) do Fed (o sistema de bancos centrais dos EUA), com base na remuneração dos Federal Funds, que são os títulos que lastreiam empréstimos interbancários overnight e que têm como finalidade a manutenção do nível das reservas bancárias depositadas no banco central.
Ao reduzir a taxa básica de juros da economia, as empresas tendem a preferir investir os recursos em aumento de produção, contratação de pessoal, pesquisa etc porque o retorno do investimento pode ser maior do que o que é pago pelo governo e/ou porque tomar empréstimos fica mais barato. Ao mesmo tempo, as famílias também conseguem crédito mais barato para consumir através de parcelamento mais barato. Esse efeito causa aumento da atividade econômica, riqueza e emprego do país através do aumenta da demanda e oferta de produtos e serviços. Por outro lado, também causa, como efeito colateral, o aumento de preços, ou inflação.
Ao aumentar a taxa de juros, os consumidores tendem a diminuir o consumo devido ao alto preço dos empréstimos e as empresas tendem a emprestar para o governo, ao invés de financiarem suas operações. Nesse caso, o efeito colateral é a queda (ou manutenção) dos preços.
Taxa preferencial de juros[editar | editar código-fonte]
A taxa preferencial de juros (em inglês, prime rate) é a taxa de juros bancária cobrada dos clientes preferenciais, isto é, aqueles que têm as melhores avaliações de crédito. É determinada pelas condições de mercado (custos bancários, expectativas inflacionárias, remuneração de outros ativos, etc.). Em geral, a taxa preferencial de juros adotada por grandes bancos tende a ser a referência para todo o setor bancário e normalmente será a menor taxa do mercado.[5]
Geralmente a taxa preferencial supera em alguns pontos a taxa básica. Mas, na Inglaterra e na Eurozona, a taxa preferencial de juros corresponde exatamente à taxa vigente no mercado interbancário, e funciona como taxa básica de juros. É o caso da Libor e da Euribor. A Libor (London Interbank Offered Rate) é a taxa preferencial de juros que remunera grandes empréstimos entre os bancos internacionais operantes no mercado londrino e é também utilizada como base da remuneração de empréstimos em dólar a empresas e instituições governamentais. Euribor (Euro Interbank Offered Rate) é a taxa de juros usada nas operações interbancárias, feitas em euro, entre os países da Eurozona.[6]
Juros simples[editar | editar código-fonte]
No regime dos juros simples, a taxa de juros é aplicada sobre o valor inicial de forma linear em todos os períodos, ou seja, não considera que o valor sobre o qual incidem juros muda ao longo do tempo.
A fórmula de juros simples pode ser escrita da seguinte maneira:
- Valor Futuro
- Valor Presente
- Taxa de juros
- Número de períodos
Exemplo
Uma pessoa toma emprestado $100 () para pagar em 2 meses () com taxa de juros de 10% ao mês (), calculados conforme o regime de juros simples. Depois de 2 meses essa pessoa irá pagar $120, conforme a fórmula:
Obtendo-se o valor dos juros diretamente
Uma pessoa toma emprestado $100 () para pagar em 2 meses () com taxa de juros de 10% ao mês (). Depois de 2 meses essa pessoa irá pagar $20 de juros, conforme a fórmula:
- Valor dos Juros
Juros compostos[editar | editar código-fonte]
No regime de juros compostos, os juros corrigíveis de cada período são somados ao capital para o cálculo de novos juros nos períodos seguintes. Nesse caso, o valor da dívida é sempre corrigida e a taxa de juros é calculada sobre esse novo valor. A fórmula de juros compostos pode ser escrita da seguinte maneira:
- Valor Futuro
- Valor Presente
- Taxa de juros
- Número de períodos
Exemplo: Uma pessoa toma emprestado $ 100 () com taxa de juros de 10% ao mês (), calculados conforme o regime de juros compostos. Depois de 2 meses () essa pessoa irá pagar $121, conforme a fórmula:
Para o caso mais geral, quando o juro é capitalizado mais de que uma vez por período, a fórmula é
onde,
- Valor Futuro
- Valor Presente
- taxa de juro nominal para o período
- número de vezes que o juro é capitalizado por período
- número de períodos
Cálculo do montante de juros a partir do capital
A partir da expressão abaixo, dado o capital, a taxa e o tempo de capitalização, se obtém diretamente o montante dos juros.
Rendas certas[editar | editar código-fonte]
Rendas Certas, Aplicações Constantes ou Anuidades são termos que se referem a aplicações sucessivas de capital (), remunerado a uma taxa de juros (), durante um período de tempo (), onde valor e taxa são constantes em cada período, segundo a fórmula.
Essa fórmula se baseia no cálculo da parcela na Tabela Price.
Exemplo ilustrativo:
Uma pessoa inicia uma poupança aplicando mensalmente $100, com rendimento de 1% ao mês. Ao fazer o 12º depósito qual será o seu saldo?
- É importante ter em mente que no caso acima o último depósito não é capitalizado, ou seja, o último valor se acumula ao montante mas não tem ainda juro de remuneração.
Propriedades multiplicativas em rendas certas
Outra forma de se chegar no valor do montante de renda () é com o produto da aplicação periódica () e somatório dos Fatores que, por sua vez, representam o crescimento dos valores aplicados ao longo do tempo ()
Exemplo:
Um plano de previdência com depósitos de $100 constantes, durante 4 meses, a uma taxa de 1% a.m. (ao mês) acumula o montante aproximado de:
Na tabela abaixo temos o somatório dos fatores de 1% de juros, então, basta aplicar a expressão acima:
| Período() | Fator | |
|---|---|---|
Montante/renda acumulada
Nessa forma de cálculo, diferentemente da primeira, o valor final é referente à situação 1 mês depois do último depósito.
Taxa de juros continuamente composta[editar | editar código-fonte]
O regime de juros compostos também pode ser expresso através da taxa de juros continuamente composta. Apesar de ter o mesmo funcionamento do regime de juros compostos, a taxa de juros continuamente composta apresenta uma fórmula de cálculo diferente:
- Valor Futuro
- Valor Presente
- Taxa de juros continuamente composta
- Número de períodos
- Número de Euler, que é equivalente a 2,718281828459...
O valor da taxa de juros , que é continuamente composta, possui significado diferente do valor da taxa de juros , usada nas fórmulas anteriores. Porém, como ambas são usadas no regime de juros compostos, existe uma equação para fazer a "tradução" de uma taxa para outra:
ou, invertendo os termos,
Diferente da taxa de juros composta, a taxa de juros continuamente composta pode ser somada. Por exemplo, se a taxa de juros continuamente composta de janeiro é 3% e a de fevereiro é 4%, a taxa desse bimestre é 7% (esse cálculo não pode ser feito com taxas que não são continuamente compostas). Devido a essa propriedade, elas podem ser usadas para facilitar a interpretação e o tratamento de bases de dados. Além disso, alguns modelos estatísticos em finanças como Teoria moderna do portfólio, Black-Scholes e Modelo de precificação de ativos financeiros (CAPM) usam esse conceito de taxa de juros nas suas premissas.
Apesar dessas vantagens, o uso da taxa continuamente composta está concentrado na área acadêmica e no mercado de capitais. Devido à dificuldade de interpretação e cálculo, essa forma de cálculo não é usada para divulgar taxa de empréstimos bancários nem tabelas de rentabilidade de investimentos para o público geral.
Exemplo numérico:
Uma pessoa toma emprestado $100 () com taxa de juros continuamente composta de 10% ao mês (). Depois de 2 meses () essa pessoa irá pagar $122,14, conforme a fórmula:
Juros simples vs. compostos[editar | editar código-fonte]

A tabela abaixo mostra os valores de um empréstimo de 100 (Euros ou Reais) com taxa de juros de 10% ao período sob o regime de juros simples e juros compostos. Note que essa tabela apresenta três momentos diferentes:
- Para períodos inferiores a 1 (), o regime de juros simples apresenta valores superiores ao regime de juros compostos.
- No período 1, o valor é igual para ambos regimes.
- Para mais de um período, o regime de juros compostos apresenta valores superiores ao regime de juros simples.
| Juros Simples | Juros Compostos | |
|---|---|---|
| 0,00 | 100,00 | 100,00 |
| 0,25 | 102,50 | 102,41 |
| 0,50 | 105,00 | 104,88 |
| 0,75 | 107,50 | 107,41 |
| 1,00 | 110,00 | 110,00 |
| 1,25 | 112,50 | 112,65 |
| 1,50 | 115,00 | 115,37 |
| 1,75 | 117,50 | 118,15 |
| 2,00 | 120,00 | 121,00 |
| 2,25 | 122,50 | 123,92 |
Enquanto que o juro simples obedece a uma progressão aritmética, que para o caso da tabela acima o capital devido é dado por:
já o juro composto obedece a uma progressão geométrica, que para a tabela acima, o capital devido é:
Taxa nominal vs. taxa real[editar | editar código-fonte]
A taxa de juros nominal é remuneração do empréstimo como foi explicado até este ponto. A taxa de juro real leva em consideração a variação verificada no índice de preços, reflectindo a alteração no poder de compra do dinheiro. O seu cálculo advém da equação de Fisher:
- Taxa de juros real
- Taxa de juros nominal
- Taxa de inflação
Exemplo numérico:
Durante um ano, uma pessoa contrai um empréstimo com uma taxa de juro nominal de 10% (), e durante o mesmo período o índice de preços cresce 5% - ou seja, a inflação é de 5% (). A taxa de juros real nesse caso é de 4,76%, conforme a fórmula:
Taxa de juros natural[editar | editar código-fonte]
A taxa de juros natural é a taxa de juros de equilíbrio entre poupança e investimento no pleno emprego da economia. Trata-se de uma variável não observável, mas existem alguns métodos para estimá-la:
- o estatístico, no qual se utiliza algum filtro da taxa de juros real para extrair o componente de tendência, que é identificado com a taxa natural;
- do modelo do agente representativo, que se baseia na teoria econômica, que entende que taxa de juros natural depende de três parâmetros, a taxa de preferência, a elasticidade de substituição do consumo e a taxa prevista do crescimento da produtividade da mão de obra. A utilização desse método não é adequado em pequenas economias abertas;
- segundo os modelos de Mundell-Fleming e de Gerações Superpostas,[7] a taxa natural de uma economia aberta pequena é igual a taxa de juros real internacional, sendo que em países nos quais existem restrições a mobilidade de capital deve-se adicionar os prêmios de risco apropriados.[8]
Tabela Financeira[editar | editar código-fonte]
A tabela financeira apresenta os fatores de juros de taxas, segundo o regime de juros compostos, dado pela fórmula básica.
onde:
deve ser expresso em forma fracional (). Exemplo: 1% = 0,01
período de capitalização
A tabela financeira é muito utilizada para se preestabelecer, por exemplo, como serão considerados os valores decimais de cada taxa, isto é, quantas casas decimais serão acordadas para os cálculos financeiros.
| Períodos | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| % | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 0,25 | 1,0050 | 1,0075 | 1,0100 | 1,0126 | 1,0151 | 1,0176 | 1,0202 | 1,0227 | 1,0253 | 1,0278 | 1,0304 |
| 0,50 | 1,0100 | 1,0151 | 1,0202 | 1,0253 | 1,0304 | 1,0355 | 1,0407 | 1,0459 | 1,0511 | 1,0564 | 1,0617 |
| 0,75 | 1,0151 | 1,0227 | 1,0303 | 1,0381 | 1,0459 | 1,0537 | 1,0616 | 1,0696 | 1,0776 | 1,0857 | 1,0938 |
| 1,00 | 1,0201 | 1,0303 | 1,0406 | 1,0510 | 1,0615 | 1,0721 | 1,0829 | 1,0937 | 1,1046 | 1,1157 | 1,1268 |
| 1,25 | 1,0252 | 1,0380 | 1,0509 | 1,0641 | 1,0774 | 1,0909 | 1,1045 | 1,1183 | 1,1323 | 1,1464 | 1,1608 |
| 1,50 | 1,0302 | 1,0457 | 1,0614 | 1,0773 | 1,0934 | 1,1098 | 1,1265 | 1,1434 | 1,1605 | 1,1779 | 1,1956 |
| 1,75 | 1,0353 | 1,0534 | 1,0719 | 1,0906 | 1,1097 | 1,1291 | 1,1489 | 1,1690 | 1,1894 | 1,2103 | 1,2314 |
| 2,00 | 1,0404 | 1,0612 | 1,0824 | 1,1041 | 1,1262 | 1,1487 | 1,1717 | 1,1951 | 1,2190 | 1,2434 | 1,2682 |
| 2,25 | 1,0455 | 1,0690 | 1,0931 | 1,1177 | 1,1428 | 1,1685 | 1,1948 | 1,2217 | 1,2492 | 1,2773 | 1,3060 |
| 2,50 | 1,0506 | 1,0769 | 1,1038 | 1,1314 | 1,1597 | 1,1887 | 1,2184 | 1,2489 | 1,2801 | 1,3121 | 1,3449 |
| 2,75 | 1,0558 | 1,0848 | 1,1146 | 1,1453 | 1,1768 | 1,2091 | 1,2424 | 1,2765 | 1,3117 | 1,3477 | 1,3848 |
| 3,00 | 1,0609 | 1,0927 | 1,1255 | 1,1593 | 1,1941 | 1,2299 | 1,2668 | 1,3048 | 1,3439 | 1,3842 | 1,4258 |
| 3,25 | 1,0661 | 1,1007 | 1,1365 | 1,1734 | 1,2115 | 1,2509 | 1,2916 | 1,3336 | 1,3769 | 1,4216 | 1,4678 |
| 3,50 | 1,0712 | 1,1087 | 1,1475 | 1,1877 | 1,2293 | 1,2723 | 1,3168 | 1,3629 | 1,4106 | 1,4600 | 1,5111 |
| 3,75 | 1,0764 | 1,1168 | 1,1587 | 1,2021 | 1,2472 | 1,2939 | 1,3425 | 1,3928 | 1,4450 | 1,4992 | 1,5555 |
| 4,00 | 1,0816 | 1,1249 | 1,1699 | 1,2167 | 1,2653 | 1,3159 | 1,3686 | 1,4233 | 1,4802 | 1,5395 | 1,6010 |
| 4,25 | 1,0868 | 1,1330 | 1,1811 | 1,2313 | 1,2837 | 1,3382 | 1,3951 | 1,4544 | 1,5162 | 1,5807 | 1,6478 |
| 4,50 | 1,0920 | 1,1412 | 1,1925 | 1,2462 | 1,3023 | 1,3609 | 1,4221 | 1,4861 | 1,5530 | 1,6229 | 1,6959 |
| 4,75 | 1,0973 | 1,1494 | 1,2040 | 1,2612 | 1,3211 | 1,3838 | 1,4495 | 1,5184 | 1,5905 | 1,6661 | 1,7452 |
| 5,00 | 1,1025 | 1,1576 | 1,2155 | 1,2763 | 1,3401 | 1,4071 | 1,4775 | 1,5513 | 1,6289 | 1,7103 | 1,7959 |
| 5,25 | 1,1078 | 1,1659 | 1,2271 | 1,2915 | 1,3594 | 1,4307 | 1,5058 | 1,5849 | 1,6681 | 1,7557 | 1,8478 |
| 5,50 | 1,1130 | 1,1742 | 1,2388 | 1,3070 | 1,3788 | 1,4547 | 1,5347 | 1,6191 | 1,7081 | 1,8021 | 1,9012 |
| 5,75 | 1,1183 | 1,1826 | 1,2506 | 1,3225 | 1,3986 | 1,4790 | 1,5640 | 1,6540 | 1,7491 | 1,8496 | 1,9560 |
| 6,00 | 1,1236 | 1,1910 | 1,2625 | 1,3382 | 1,4185 | 1,5036 | 1,5938 | 1,6895 | 1,7908 | 1,8983 | 2,0122 |
| 6,25 | 1,1289 | 1,1995 | 1,2744 | 1,3541 | 1,4387 | 1,5286 | 1,6242 | 1,7257 | 1,8335 | 1,9481 | 2,0699 |
| 6,50 | 1,1342 | 1,2079 | 1,2865 | 1,3701 | 1,4591 | 1,5540 | 1,6550 | 1,7626 | 1,8771 | 1,9992 | 2,1291 |
| 6,75 | 1,1396 | 1,2165 | 1,2986 | 1,3862 | 1,4798 | 1,5797 | 1,6863 | 1,8002 | 1,9217 | 2,0514 | 2,1899 |
| 7,00 | 1,1449 | 1,2250 | 1,3108 | 1,4026 | 1,5007 | 1,6058 | 1,7182 | 1,8385 | 1,9672 | 2,1049 | 2,2522 |
| 7,25 | 1,1503 | 1,2336 | 1,3231 | 1,4190 | 1,5219 | 1,6322 | 1,7506 | 1,8775 | 2,0136 | 2,1596 | 2,3162 |
| 7,50 | 1,1556 | 1,2423 | 1,3355 | 1,4356 | 1,5433 | 1,6590 | 1,7835 | 1,9172 | 2,0610 | 2,2156 | 2,3818 |
| 7,75 | 1,1610 | 1,2510 | 1,3479 | 1,4524 | 1,5650 | 1,6862 | 1,8169 | 1,9577 | 2,1095 | 2,2730 | 2,4491 |
| 8,00 | 1,1664 | 1,2597 | 1,3605 | 1,4693 | 1,5869 | 1,7138 | 1,8509 | 1,9990 | 2,1589 | 2,3316 | 2,5182 |
| 8,25 | 1,1718 | 1,2685 | 1,3731 | 1,4864 | 1,6090 | 1,7418 | 1,8855 | 2,0410 | 2,2094 | 2,3917 | 2,5890 |
| 8,50 | 1,1772 | 1,2773 | 1,3859 | 1,5037 | 1,6315 | 1,7701 | 1,9206 | 2,0839 | 2,2610 | 2,4532 | 2,6617 |
| 8,75 | 1,1827 | 1,2861 | 1,3987 | 1,5211 | 1,6542 | 1,7989 | 1,9563 | 2,1275 | 2,3136 | 2,5161 | 2,7362 |
| 9,00 | 1,1881 | 1,2950 | 1,4116 | 1,5386 | 1,6771 | 1,8280 | 1,9926 | 2,1719 | 2,3674 | 2,5804 | 2,8127 |
| 9,25 | 1,1936 | 1,3040 | 1,4246 | 1,5563 | 1,7003 | 1,8576 | 2,0294 | 2,2171 | 2,4222 | 2,6463 | 2,8911 |
| 9,50 | 1,1990 | 1,3129 | 1,4377 | 1,5742 | 1,7238 | 1,8876 | 2,0669 | 2,2632 | 2,4782 | 2,7137 | 2,9715 |
| 9,75 | 1,2045 | 1,3219 | 1,4508 | 1,5923 | 1,7475 | 1,9179 | 2,1049 | 2,3102 | 2,5354 | 2,7826 | 3,0539 |
| 10,00 | 1,2100 | 1,3310 | 1,4641 | 1,6105 | 1,7716 | 1,9487 | 2,1436 | 2,3579 | 2,5937 | 2,8531 | 3,1384 |
| 10,25 | 1,2155 | 1,3401 | 1,4775 | 1,6289 | 1,7959 | 1,9799 | 2,1829 | 2,4066 | 2,6533 | 2,9253 | 3,2251 |
| 10,50 | 1,2210 | 1,3492 | 1,4909 | 1,6474 | 1,8204 | 2,0116 | 2,2228 | 2,4562 | 2,7141 | 2,9991 | 3,3140 |
| 10,75 | 1,2266 | 1,3584 | 1,5044 | 1,6662 | 1,8453 | 2,0436 | 2,2633 | 2,5066 | 2,7761 | 3,0745 | 3,4051 |
| 11,00 | 1,2321 | 1,3676 | 1,5181 | 1,6851 | 1,8704 | 2,0762 | 2,3045 | 2,5580 | 2,8394 | 3,1518 | 3,4985 |
| 11,25 | 1,2377 | 1,3769 | 1,5318 | 1,7041 | 1,8958 | 2,1091 | 2,3464 | 2,6104 | 2,9040 | 3,2307 | 3,5942 |
| 11,50 | 1,2432 | 1,3862 | 1,5456 | 1,7234 | 1,9215 | 2,1425 | 2,3889 | 2,6636 | 2,9699 | 3,3115 | 3,6923 |
| 11,75 | 1,2488 | 1,3955 | 1,5595 | 1,7428 | 1,9475 | 2,1764 | 2,4321 | 2,7179 | 3,0372 | 3,3941 | 3,7929 |
| 12,00 | 1,2544 | 1,4049 | 1,5735 | 1,7623 | 1,9738 | 2,2107 | 2,4760 | 2,7731 | 3,1058 | 3,4785 | 3,8960 |
| 12,25 | 1,2600 | 1,4144 | 1,5876 | 1,7821 | 2,0004 | 2,2455 | 2,5205 | 2,8293 | 3,1759 | 3,5649 | 4,0016 |
| 12,50 | 1,2656 | 1,4238 | 1,6018 | 1,8020 | 2,0273 | 2,2807 | 2,5658 | 2,8865 | 3,2473 | 3,6532 | 4,1099 |
| 12,75 | 1,2713 | 1,4333 | 1,6161 | 1,8221 | 2,0545 | 2,3164 | 2,6118 | 2,9448 | 3,3202 | 3,7435 | 4,2208 |
| 13,00 | 1,2769 | 1,4429 | 1,6305 | 1,8424 | 2,0820 | 2,3526 | 2,6584 | 3,0040 | 3,3946 | 3,8359 | 4,3345 |
| 13,25 | 1,2826 | 1,4525 | 1,6450 | 1,8629 | 2,1097 | 2,3893 | 2,7059 | 3,0644 | 3,4704 | 3,9303 | 4,4510 |
| 13,50 | 1,2882 | 1,4621 | 1,6595 | 1,8836 | 2,1378 | 2,4264 | 2,7540 | 3,1258 | 3,5478 | 4,0267 | 4,5704 |
| 13,75 | 1,2939 | 1,4718 | 1,6742 | 1,9044 | 2,1662 | 2,4641 | 2,8029 | 3,1883 | 3,6267 | 4,1254 | 4,6926 |
| 14,00 | 1,2996 | 1,4815 | 1,6890 | 1,9254 | 2,1950 | 2,5023 | 2,8526 | 3,2519 | 3,7072 | 4,2262 | 4,8179 |
| 14,25 | 1,3053 | 1,4913 | 1,7038 | 1,9466 | 2,2240 | 2,5409 | 2,9030 | 3,3167 | 3,7893 | 4,3293 | 4,9462 |
| 14,50 | 1,3110 | 1,5011 | 1,7188 | 1,9680 | 2,2534 | 2,5801 | 2,9542 | 3,3826 | 3,8731 | 4,4347 | 5,0777 |
| 14,75 | 1,3168 | 1,5110 | 1,7338 | 1,9896 | 2,2831 | 2,6198 | 3,0062 | 3,4496 | 3,9585 | 4,5423 | 5,2123 |
| 15,00 | 1,3225 | 1,5209 | 1,7490 | 2,0114 | 2,3131 | 2,6600 | 3,0590 | 3,5179 | 4,0456 | 4,6524 | 5,3503 |
| 15,25 | 1,3283 | 1,5308 | 1,7643 | 2,0333 | 2,3434 | 2,7008 | 3,1126 | 3,5873 | 4,1344 | 4,7649 | 5,4915 |
| 15,50 | 1,3340 | 1,5408 | 1,7796 | 2,0555 | 2,3741 | 2,7420 | 3,1671 | 3,6580 | 4,2249 | 4,8798 | 5,6362 |
| 15,75 | 1,3398 | 1,5508 | 1,7951 | 2,0778 | 2,4051 | 2,7839 | 3,2223 | 3,7298 | 4,3173 | 4,9972 | 5,7843 |
| 16,00 | 1,3456 | 1,5609 | 1,8106 | 2,1003 | 2,4364 | 2,8262 | 3,2784 | 3,8030 | 4,4114 | 5,1173 | 5,9360 |
| 16,25 | 1,3514 | 1,5710 | 1,8263 | 2,1231 | 2,4681 | 2,8691 | 3,3354 | 3,8774 | 4,5074 | 5,2399 | 6,0914 |
| 16,50 | 1,3572 | 1,5812 | 1,8421 | 2,1460 | 2,5001 | 2,9126 | 3,3932 | 3,9531 | 4,6053 | 5,3652 | 6,2504 |
| 16,75 | 1,3631 | 1,5914 | 1,8579 | 2,1691 | 2,5325 | 2,9566 | 3,4519 | 4,0301 | 4,7051 | 5,4932 | 6,4133 |
| 17,00 | 1,3689 | 1,6016 | 1,8739 | 2,1924 | 2,5652 | 3,0012 | 3,5115 | 4,1084 | 4,8068 | 5,6240 | 6,5801 |
| 17,25 | 1,3748 | 1,6119 | 1,8900 | 2,2160 | 2,5982 | 3,0464 | 3,5719 | 4,1881 | 4,9105 | 5,7576 | 6,7508 |
| 17,50 | 1,3806 | 1,6222 | 1,9061 | 2,2397 | 2,6316 | 3,0922 | 3,6333 | 4,2691 | 5,0162 | 5,8941 | 6,9256 |
| 17,75 | 1,3865 | 1,6326 | 1,9224 | 2,2636 | 2,6654 | 3,1385 | 3,6956 | 4,3516 | 5,1240 | 6,0335 | 7,1045 |
| 18,00 | 1,3924 | 1,6430 | 1,9388 | 2,2878 | 2,6996 | 3,1855 | 3,7589 | 4,4355 | 5,2338 | 6,1759 | 7,2876 |
| 18,25 | 1,3983 | 1,6535 | 1,9553 | 2,3121 | 2,7341 | 3,2330 | 3,8230 | 4,5207 | 5,3458 | 6,3214 | 7,4750 |
| 18,50 | 1,4042 | 1,6640 | 1,9718 | 2,3366 | 2,7689 | 3,2812 | 3,8882 | 4,6075 | 5,4599 | 6,4700 | 7,6669 |
| 18,75 | 1,4102 | 1,6746 | 1,9885 | 2,3614 | 2,8042 | 3,3299 | 3,9543 | 4,6957 | 5,5762 | 6,6217 | 7,8633 |
| 19,00 | 1,4161 | 1,6852 | 2,0053 | 2,3864 | 2,8398 | 3,3793 | 4,0214 | 4,7854 | 5,6947 | 6,7767 | 8,0642 |
| 19,25 | 1,4221 | 1,6958 | 2,0222 | 2,4115 | 2,8757 | 3,4293 | 4,0895 | 4,8767 | 5,8155 | 6,9349 | 8,2699 |
| 19,50 | 1,4280 | 1,7065 | 2,0393 | 2,4369 | 2,9121 | 3,4800 | 4,1586 | 4,9695 | 5,9385 | 7,0965 | 8,4804 |
| 19,75 | 1,4340 | 1,7172 | 2,0564 | 2,4625 | 2,9489 | 3,5313 | 4,2287 | 5,0638 | 6,0639 | 7,2616 | 8,6957 |
| 20,00 | 1,4400 | 1,7280 | 2,0736 | 2,4883 | 2,9860 | 3,5832 | 4,2998 | 5,1598 | 6,1917 | 7,4301 | 8,9161 |
| 20,25 | 1,4460 | 1,7388 | 2,0909 | 2,5143 | 3,0235 | 3,6358 | 4,3720 | 5,2573 | 6,3219 | 7,6021 | 9,1416 |
| 20,50 | 1,4520 | 1,7497 | 2,1084 | 2,5406 | 3,0614 | 3,6890 | 4,4453 | 5,3565 | 6,4546 | 7,7778 | 9,3723 |
| 20,75 | 1,4581 | 1,7606 | 2,1259 | 2,5671 | 3,0997 | 3,7429 | 4,5196 | 5,4574 | 6,5898 | 7,9572 | 9,6083 |
| 21,00 | 1,4641 | 1,7716 | 2,1436 | 2,5937 | 3,1384 | 3,7975 | 4,5950 | 5,5599 | 6,7275 | 8,1403 | 9,8497 |
| 21,25 | 1,4702 | 1,7826 | 2,1614 | 2,6206 | 3,1775 | 3,8528 | 4,6715 | 5,6642 | 6,8678 | 8,3272 | 10,0967 |
| 21,50 | 1,4762 | 1,7936 | 2,1792 | 2,6478 | 3,2170 | 3,9087 | 4,7491 | 5,7701 | 7,0107 | 8,5180 | 10,3494 |
| 21,75 | 1,4823 | 1,8047 | 2,1972 | 2,6751 | 3,2570 | 3,9654 | 4,8278 | 5,8779 | 7,1563 | 8,7128 | 10,6079 |
| 22,00 | 1,4884 | 1,8158 | 2,2153 | 2,7027 | 3,2973 | 4,0227 | 4,9077 | 5,9874 | 7,3046 | 8,9117 | 10,8722 |
| 22,25 | 1,4945 | 1,8270 | 2,2335 | 2,7305 | 3,3381 | 4,0808 | 4,9887 | 6,0987 | 7,4557 | 9,1146 | 11,1426 |
| 22,50 | 1,5006 | 1,8383 | 2,2519 | 2,7585 | 3,3792 | 4,1395 | 5,0709 | 6,2119 | 7,6096 | 9,3217 | 11,4191 |
| 22,75 | 1,5068 | 1,8495 | 2,2703 | 2,7868 | 3,4208 | 4,1990 | 5,1543 | 6,3269 | 7,7663 | 9,5332 | 11,7019 |
| 23,00 | 1,5129 | 1,8609 | 2,2889 | 2,8153 | 3,4628 | 4,2593 | 5,2389 | 6,4439 | 7,9259 | 9,7489 | 11,9912 |
| 23,25 | 1,5191 | 1,8722 | 2,3075 | 2,8440 | 3,5053 | 4,3202 | 5,3247 | 6,5627 | 8,0885 | 9,9691 | 12,2869 |
| 23,50 | 1,5252 | 1,8837 | 2,3263 | 2,8730 | 3,5481 | 4,3820 | 5,4117 | 6,6835 | 8,2541 | 10,1938 | 12,5894 |
| 23,75 | 1,5314 | 1,8951 | 2,3452 | 2,9022 | 3,5915 | 4,4444 | 5,5000 | 6,8062 | 8,4227 | 10,4231 | 12,8986 |
| 24,00 | 1,5376 | 1,9066 | 2,3642 | 2,9316 | 3,6352 | 4,5077 | 5,5895 | 6,9310 | 8,5944 | 10,6571 | 13,2148 |
| 24,25 | 1,5438 | 1,9182 | 2,3833 | 2,9613 | 3,6794 | 4,5717 | 5,6803 | 7,0578 | 8,7693 | 10,8958 | 13,5381 |
| 24,50 | 1,5500 | 1,9298 | 2,4026 | 2,9912 | 3,7241 | 4,6364 | 5,7724 | 7,1866 | 8,9473 | 11,1394 | 13,8686 |
| 24,75 | 1,5563 | 1,9414 | 2,4219 | 3,0214 | 3,7691 | 4,7020 | 5,8658 | 7,3175 | 9,1286 | 11,3880 | 14,2065 |
| 25,00 | 1,5625 | 1,9531 | 2,4414 | 3,0518 | 3,8147 | 4,7684 | 5,9605 | 7,4506 | 9,3132 | 11,6415 | 14,5519 |
| 25,25 | 1,5688 | 1,9649 | 2,4610 | 3,0824 | 3,8607 | 4,8355 | 6,0565 | 7,5858 | 9,5012 | 11,9002 | 14,9050 |
| 25,50 | 1,5750 | 1,9767 | 2,4807 | 3,1133 | 3,9072 | 4,9035 | 6,1539 | 7,7231 | 9,6925 | 12,1641 | 15,2660 |
| 25,75 | 1,5813 | 1,9885 | 2,5005 | 3,1444 | 3,9541 | 4,9723 | 6,2526 | 7,8627 | 9,8874 | 12,4333 | 15,6349 |
| 26,00 | 1,5876 | 2,0004 | 2,5205 | 3,1758 | 4,0015 | 5,0419 | 6,3528 | 8,0045 | 10,0857 | 12,7080 | 16,0120 |
| 26,25 | 1,5939 | 2,0123 | 2,5405 | 3,2074 | 4,0494 | 5,1123 | 6,4543 | 8,1486 | 10,2876 | 12,9881 | 16,3975 |
| 26,50 | 1,6002 | 2,0243 | 2,5607 | 3,2393 | 4,0977 | 5,1836 | 6,5573 | 8,2950 | 10,4931 | 13,2738 | 16,7914 |
| 26,75 | 1,6066 | 2,0363 | 2,5810 | 3,2714 | 4,1466 | 5,2558 | 6,6617 | 8,4437 | 10,7024 | 13,5652 | 17,1939 |
| 27,00 | 1,6129 | 2,0484 | 2,6014 | 3,3038 | 4,1959 | 5,3288 | 6,7675 | 8,5948 | 10,9153 | 13,8625 | 17,6053 |
| 27,25 | 1,6193 | 2,0605 | 2,6220 | 3,3365 | 4,2457 | 5,4026 | 6,8748 | 8,7482 | 11,1321 | 14,1656 | 18,0258 |
| 27,50 | 1,6256 | 2,0727 | 2,6427 | 3,3694 | 4,2960 | 5,4774 | 6,9836 | 8,9041 | 11,3528 | 14,4748 | 18,4553 |
| 27,75 | 1,6320 | 2,0849 | 2,6634 | 3,4026 | 4,3468 | 5,5530 | 7,0939 | 9,0625 | 11,5773 | 14,7901 | 18,8943 |
| 28,00 | 1,6384 | 2,0972 | 2,6844 | 3,4360 | 4,3980 | 5,6295 | 7,2058 | 9,2234 | 11,8059 | 15,1116 | 19,3428 |
| 28,25 | 1,6448 | 2,1095 | 2,7054 | 3,4697 | 4,4498 | 5,7069 | 7,3191 | 9,3868 | 12,0385 | 15,4394 | 19,8011 |
| 28,50 | 1,6512 | 2,1218 | 2,7265 | 3,5036 | 4,5021 | 5,7852 | 7,4340 | 9,5527 | 12,2753 | 15,7737 | 20,2692 |
| 28,75 | 1,6577 | 2,1342 | 2,7478 | 3,5378 | 4,5549 | 5,8645 | 7,5505 | 9,7213 | 12,5162 | 16,1146 | 20,7476 |
| 29,00 | 1,6641 | 2,1467 | 2,7692 | 3,5723 | 4,6083 | 5,9447 | 7,6686 | 9,8925 | 12,7614 | 16,4622 | 21,2362 |
| 29,25 | 1,6706 | 2,1592 | 2,7908 | 3,6071 | 4,6621 | 6,0258 | 7,7883 | 10,0664 | 13,0108 | 16,8165 | 21,7353 |
| 29,50 | 1,6770 | 2,1717 | 2,8124 | 3,6421 | 4,7165 | 6,1079 | 7,9097 | 10,2430 | 13,2647 | 17,1778 | 22,2452 |
| 29,75 | 1,6835 | 2,1843 | 2,8342 | 3,6774 | 4,7714 | 6,1909 | 8,0327 | 10,4224 | 13,5230 | 17,5461 | 22,7661 |
| 30,00 | 1,6900 | 2,1970 | 2,8561 | 3,7129 | 4,8268 | 6,2749 | 8,1573 | 10,6045 | 13,7858 | 17,9216 | 23,2981 |
| 30,25 | 1,6965 | 2,2097 | 2,8781 | 3,7488 | 4,8828 | 6,3598 | 8,2837 | 10,7895 | 14,0533 | 18,3044 | 23,8415 |
| 30,50 | 1,7030 | 2,2224 | 2,9003 | 3,7849 | 4,9393 | 6,4458 | 8,4117 | 10,9773 | 14,3253 | 18,6946 | 24,3964 |
| 30,75 | 1,7096 | 2,2352 | 2,9226 | 3,8213 | 4,9963 | 6,5327 | 8,5415 | 11,1680 | 14,6022 | 19,0923 | 24,9632 |
| 31,00 | 1,7161 | 2,2481 | 2,9450 | 3,8579 | 5,0539 | 6,6206 | 8,6730 | 11,3617 | 14,8838 | 19,4977 | 25,5420 |
| 31,25 | 1,7227 | 2,2610 | 2,9675 | 3,8949 | 5,1121 | 6,7096 | 8,8063 | 11,5583 | 15,1703 | 19,9110 | 26,1331 |
| 31,50 | 1,7292 | 2,2739 | 2,9902 | 3,9321 | 5,1708 | 6,7996 | 8,9414 | 11,7580 | 15,4617 | 20,3321 | 26,7368 |
| 31,75 | 1,7358 | 2,2869 | 3,0130 | 3,9697 | 5,2300 | 6,8906 | 9,0783 | 11,9607 | 15,7582 | 20,7614 | 27,3532 |
| 32,00 | 1,7424 | 2,3000 | 3,0360 | 4,0075 | 5,2899 | 6,9826 | 9,2170 | 12,1665 | 16,0598 | 21,1989 | 27,9825 |
| 32,25 | 1,7490 | 2,3131 | 3,0590 | 4,0456 | 5,3503 | 7,0757 | 9,3576 | 12,3755 | 16,3665 | 21,6447 | 28,6252 |
| 32,50 | 1,7556 | 2,3262 | 3,0822 | 4,0839 | 5,4112 | 7,1699 | 9,5001 | 12,5876 | 16,6786 | 22,0991 | 29,2813 |
| 32,75 | 1,7623 | 2,3394 | 3,1055 | 4,1226 | 5,4728 | 7,2651 | 9,6444 | 12,8030 | 16,9959 | 22,5621 | 29,9512 |
| 33,00 | 1,7689 | 2,3526 | 3,1290 | 4,1616 | 5,5349 | 7,3614 | 9,7907 | 13,0216 | 17,3187 | 23,0339 | 30,6351 |
| 33,25 | 1,7756 | 2,3659 | 3,1526 | 4,2008 | 5,5976 | 7,4588 | 9,9389 | 13,2436 | 17,6471 | 23,5147 | 31,3333 |
| 33,50 | 1,7822 | 2,3793 | 3,1763 | 4,2404 | 5,6609 | 7,5573 | 10,0890 | 13,4689 | 17,9810 | 24,0046 | 32,0461 |
| 33,75 | 1,7889 | 2,3927 | 3,2002 | 4,2802 | 5,7248 | 7,6570 | 10,2412 | 13,6976 | 18,3205 | 24,5037 | 32,7737 |
| 34,00 | 1,7956 | 2,4061 | 3,2242 | 4,3204 | 5,7893 | 7,7577 | 10,3953 | 13,9297 | 18,6659 | 25,0123 | 33,5164 |
| 34,25 | 1,8023 | 2,4196 | 3,2483 | 4,3609 | 5,8544 | 7,8596 | 10,5515 | 14,1654 | 19,0170 | 25,5304 | 34,2745 |
| 34,50 | 1,8090 | 2,4331 | 3,2726 | 4,4016 | 5,9202 | 7,9626 | 10,7097 | 14,4046 | 19,3742 | 26,0582 | 35,0483 |
| 34,75 | 1,8158 | 2,4467 | 3,2970 | 4,4427 | 5,9865 | 8,0668 | 10,8700 | 14,6473 | 19,7373 | 26,5960 | 35,8381 |
| 35,00 | 1,8225 | 2,4604 | 3,3215 | 4,4840 | 6,0534 | 8,1722 | 11,0324 | 14,8937 | 20,1066 | 27,1439 | 36,6442 |
| 35,25 | 1,8293 | 2,4741 | 3,3462 | 4,5257 | 6,1210 | 8,2787 | 11,1969 | 15,1438 | 20,4820 | 27,7019 | 37,4669 |
| 35,50 | 1,8360 | 2,4878 | 3,3710 | 4,5677 | 6,1892 | 8,3864 | 11,3636 | 15,3976 | 20,8638 | 28,2704 | 38,3064 |
| 35,75 | 1,8428 | 2,5016 | 3,3959 | 4,6100 | 6,2581 | 8,4953 | 11,5324 | 15,6552 | 21,2519 | 28,8495 | 39,1632 |
| 36,00 | 1,8496 | 2,5155 | 3,4210 | 4,6526 | 6,3275 | 8,6054 | 11,7034 | 15,9166 | 21,6466 | 29,4393 | 40,0375 |
| 36,25 | 1,8564 | 2,5294 | 3,4462 | 4,6955 | 6,3976 | 8,7168 | 11,8766 | 16,1819 | 22,0478 | 30,0401 | 40,9297 |
| 36,50 | 1,8632 | 2,5433 | 3,4716 | 4,7387 | 6,4684 | 8,8293 | 12,0521 | 16,4511 | 22,4557 | 30,6520 | 41,8400 |
| 36,75 | 1,8701 | 2,5573 | 3,4971 | 4,7823 | 6,5398 | 8,9432 | 12,2298 | 16,7242 | 22,8704 | 31,2752 | 42,7689 |
| 37,00 | 1,8769 | 2,5714 | 3,5228 | 4,8262 | 6,6119 | 9,0582 | 12,4098 | 17,0014 | 23,2919 | 31,9100 | 43,7166 |
| 37,25 | 1,8838 | 2,5855 | 3,5485 | 4,8704 | 6,6846 | 9,1746 | 12,5921 | 17,2827 | 23,7205 | 32,5564 | 44,6836 |
| 37,50 | 1,8906 | 2,5996 | 3,5745 | 4,9149 | 6,7580 | 9,2922 | 12,7768 | 17,5681 | 24,1561 | 33,2146 | 45,6701 |
| 37,75 | 1,8975 | 2,6138 | 3,6005 | 4,9597 | 6,8320 | 9,4111 | 12,9638 | 17,8577 | 24,5989 | 33,8850 | 46,6766 |
| 38,00 | 1,9044 | 2,6281 | 3,6267 | 5,0049 | 6,9068 | 9,5313 | 13,1532 | 18,1515 | 25,0490 | 34,5677 | 47,7034 |
| 38,25 | 1,9113 | 2,6424 | 3,6531 | 5,0504 | 6,9822 | 9,6529 | 13,3451 | 18,4496 | 25,5065 | 35,2628 | 48,7508 |
| 38,50 | 1,9182 | 2,6567 | 3,6796 | 5,0962 | 7,0583 | 9,7757 | 13,5394 | 18,7520 | 25,9715 | 35,9706 | 49,8193 |
| 38,75 | 1,9252 | 2,6712 | 3,7062 | 5,1424 | 7,1351 | 9,8999 | 13,7361 | 19,0589 | 26,4442 | 36,6913 | 50,9092 |
| 39,00 | 1,9321 | 2,6856 | 3,7330 | 5,1889 | 7,2125 | 10,0254 | 13,9354 | 19,3702 | 26,9245 | 37,4251 | 52,0209 |
| 39,25 | 1,9391 | 2,7001 | 3,7599 | 5,2357 | 7,2907 | 10,1523 | 14,1371 | 19,6860 | 27,4127 | 38,1722 | 53,1548 |
| 39,50 | 1,9460 | 2,7147 | 3,7870 | 5,2829 | 7,3696 | 10,2806 | 14,3415 | 20,0064 | 27,9089 | 38,9329 | 54,3113 |
| 39,75 | 1,9530 | 2,7293 | 3,8142 | 5,3304 | 7,4492 | 10,4103 | 14,5484 | 20,3314 | 28,4131 | 39,7073 | 55,4909 |
| 40,00 | 1,9600 | 2,7440 | 3,8416 | 5,3782 | 7,5295 | 10,5414 | 14,7579 | 20,6610 | 28,9255 | 40,4957 | 56,6939 |
| 40,25 | 1,9670 | 2,7587 | 3,8691 | 5,4264 | 7,6106 | 10,6738 | 14,9700 | 20,9955 | 29,4462 | 41,2982 | 57,9208 |
| 40,50 | 1,9740 | 2,7735 | 3,8968 | 5,4750 | 7,6923 | 10,8077 | 15,1849 | 21,3347 | 29,9753 | 42,1153 | 59,1720 |
| 40,75 | 1,9811 | 2,7883 | 3,9246 | 5,5239 | 7,7748 | 10,9431 | 15,4024 | 21,6788 | 30,5129 | 42,9470 | 60,4478 |
| 41,00 | 1,9881 | 2,8032 | 3,9525 | 5,5731 | 7,8580 | 11,0798 | 15,6226 | 22,0278 | 31,0593 | 43,7936 | 61,7489 |
| 41,25 | 1,9952 | 2,8182 | 3,9806 | 5,6227 | 7,9420 | 11,2181 | 15,8456 | 22,3819 | 31,6144 | 44,6553 | 63,0756 |
| 41,50 | 2,0022 | 2,8331 | 4,0089 | 5,6726 | 8,0267 | 11,3578 | 16,0713 | 22,7409 | 32,1784 | 45,5324 | 64,4284 |
| 41,75 | 2,0093 | 2,8482 | 4,0373 | 5,7229 | 8,1122 | 11,4990 | 16,2999 | 23,1051 | 32,7515 | 46,4252 | 65,8077 |
| 42,00 | 2,0164 | 2,8633 | 4,0659 | 5,7735 | 8,1984 | 11,6418 | 16,5313 | 23,4744 | 33,3337 | 47,3338 | 67,2141 |
| 42,25 | 2,0235 | 2,8784 | 4,0946 | 5,8245 | 8,2854 | 11,7860 | 16,7656 | 23,8490 | 33,9252 | 48,2586 | 68,6479 |
| 42,50 | 2,0306 | 2,8936 | 4,1234 | 5,8759 | 8,3732 | 11,9317 | 17,0027 | 24,2289 | 34,5262 | 49,1998 | 70,1097 |
| 42,75 | 2,0378 | 2,9089 | 4,1525 | 5,9276 | 8,4617 | 12,0791 | 17,2428 | 24,6142 | 35,1367 | 50,1577 | 71,6001 |
| 43,00 | 2,0449 | 2,9242 | 4,1816 | 5,9797 | 8,5510 | 12,2279 | 17,4859 | 25,0049 | 35,7569 | 51,1324 | 73,1194 |
| 43,25 | 2,0521 | 2,9396 | 4,2109 | 6,0322 | 8,6411 | 12,3783 | 17,7320 | 25,4011 | 36,3870 | 52,1244 | 74,6682 |
| 43,50 | 2,0592 | 2,9550 | 4,2404 | 6,0850 | 8,7320 | 12,5304 | 17,9811 | 25,8028 | 37,0270 | 53,1338 | 76,2470 |
| 43,75 | 2,0664 | 2,9705 | 4,2700 | 6,1382 | 8,8236 | 12,6840 | 18,2332 | 26,2102 | 37,6772 | 54,1610 | 77,8564 |
| 44,00 | 2,0736 | 2,9860 | 4,2998 | 6,1917 | 8,9161 | 12,8392 | 18,4884 | 26,6233 | 38,3376 | 55,2061 | 79,4968 |
| 44,25 | 2,0808 | 3,0016 | 4,3298 | 6,2457 | 9,0094 | 12,9960 | 18,7468 | 27,0422 | 39,0084 | 56,2696 | 81,1689 |
| 44,50 | 2,0880 | 3,0172 | 4,3598 | 6,3000 | 9,1035 | 13,1545 | 19,0083 | 27,4670 | 39,6898 | 57,3517 | 82,8732 |
| 44,75 | 2,0953 | 3,0329 | 4,3901 | 6,3547 | 9,1984 | 13,3147 | 19,2730 | 27,8976 | 40,3818 | 58,4527 | 84,6102 |
| 45,00 | 2,1025 | 3,0486 | 4,4205 | 6,4097 | 9,2941 | 13,4765 | 19,5409 | 28,3343 | 41,0847 | 59,5728 | 86,3806 |
| 45,25 | 2,1098 | 3,0644 | 4,4511 | 6,4652 | 9,3907 | 13,6400 | 19,8120 | 28,7770 | 41,7986 | 60,7124 | 88,1848 |
| 45,50 | 2,1170 | 3,0803 | 4,4818 | 6,5210 | 9,4881 | 13,8051 | 20,0865 | 29,2258 | 42,5236 | 61,8718 | 90,0235 |
| 45,75 | 2,1243 | 3,0962 | 4,5127 | 6,5772 | 9,5863 | 13,9720 | 20,3643 | 29,6809 | 43,2599 | 63,0513 | 91,8973 |
| 46,00 | 2,1316 | 3,1121 | 4,5437 | 6,6338 | 9,6854 | 14,1407 | 20,6454 | 30,1423 | 44,0077 | 64,2512 | 93,8068 |
| 46,25 | 2,1389 | 3,1282 | 4,5749 | 6,6908 | 9,7853 | 14,3110 | 20,9299 | 30,6100 | 44,7671 | 65,4719 | 95,7526 |
| 46,50 | 2,1462 | 3,1442 | 4,6063 | 6,7482 | 9,8861 | 14,4832 | 21,2178 | 31,0841 | 45,5382 | 66,7135 | 97,7353 |
| 46,75 | 2,1536 | 3,1603 | 4,6378 | 6,8060 | 9,9878 | 14,6571 | 21,5092 | 31,5648 | 46,3213 | 67,9766 | 99,7556 |
| 47,00 | 2,1609 | 3,1765 | 4,6695 | 6,8641 | 10,0903 | 14,8327 | 21,8041 | 32,0521 | 47,1165 | 69,2613 | 101,8141 |
| 47,25 | 2,1683 | 3,1928 | 4,7013 | 6,9227 | 10,1937 | 15,0102 | 22,1026 | 32,5460 | 47,9240 | 70,5681 | 103,9115 |
| 47,50 | 2,1756 | 3,2090 | 4,7333 | 6,9817 | 10,2980 | 15,1895 | 22,4045 | 33,0467 | 48,7439 | 71,8972 | 106,0484 |
| 47,75 | 2,1830 | 3,2254 | 4,7655 | 7,0411 | 10,4032 | 15,3707 | 22,7101 | 33,5542 | 49,5764 | 73,2491 | 108,2256 |
| 48,00 | 2,1904 | 3,2418 | 4,7979 | 7,1008 | 10,5092 | 15,5536 | 23,0194 | 34,0687 | 50,4217 | 74,6241 | 110,4436 |
| 48,25 | 2,1978 | 3,2582 | 4,8304 | 7,1610 | 10,6162 | 15,7385 | 23,3323 | 34,5901 | 51,2799 | 76,0224 | 112,7032 |
| 48,50 | 2,2052 | 3,2748 | 4,8630 | 7,2216 | 10,7240 | 15,9252 | 23,6489 | 35,1187 | 52,1512 | 77,4446 | 115,0052 |
| 48,75 | 2,2127 | 3,2913 | 4,8958 | 7,2826 | 10,8328 | 16,1138 | 23,9693 | 35,6544 | 53,0359 | 78,8909 | 117,3502 |
| 49,00 | 2,2201 | 3,3079 | 4,9288 | 7,3440 | 10,9425 | 16,3044 | 24,2935 | 36,1973 | 53,9340 | 80,3617 | 119,7389 |
| 49,25 | 2,2276 | 3,3246 | 4,9620 | 7,4058 | 11,0531 | 16,4968 | 24,6215 | 36,7476 | 54,8458 | 81,8574 | 122,1721 |
| 49,50 | 2,2350 | 3,3414 | 4,9953 | 7,4680 | 11,1647 | 16,6912 | 24,9534 | 37,3053 | 55,7714 | 83,3783 | 124,6506 |
| 49,75 | 2,2425 | 3,3582 | 5,0288 | 7,5307 | 11,2772 | 16,8876 | 25,2892 | 37,8705 | 56,7111 | 84,9249 | 127,1751 |
| 50,00 | 2,2500 | 3,3750 | 5,0625 | 7,5938 | 11,3906 | 17,0859 | 25,6289 | 38,4434 | 57,6650 | 86,4976 | 129,7463 |
Ver também[editar | editar código-fonte]
- Usura
- Economia
- Inflação
- Macroeconomia
- Matemática financeira
- Amortização
- Anatocismo
- Rendimento
- Seguro
Ligações externas[editar | editar código-fonte]
- Calculadora de juros compostos: Site para cálculo de juros compostos com resultado em formato gráfico e tabulado.
Notas e referências
Notas
- ↑ 356 a.C. Tito Lívio dá como cônsules M. Fábio Ambusto e T. Quíncio, e comenta que alguns analistas trocavam T. Quíncio por M. Popílio.
- ↑ No período de 1° de julho de 1996 a 4 de março de 1999, o Copom fixava a TBC (Taxa Básica do Banco Central). A partir de 5 de março de 1999, com a extinção da TBC, o Copom passou a divulgar a meta para a taxa Selic - para fins de política monetária. Boletim Copom (com informações até março de 2014), p. 8, nota 1.
Referências
- ↑ Tito Lívio, História de Roma, vii. 18. [em linha]
- ↑ Tito Lívio, História de Roma, vii. 19.
- ↑ Banco Central do Brasil - SELIC. [1]
- ↑ Banco Central do Brasil - COPOM. [2]
- ↑ Glossário da Associação dos Bancos no Distrito Federal - ASSBAN
- ↑ Conheça melhor as taxas Libor e Euribor, referências às operações interbancárias, por Roberto Altenhofen Pires Pereira. Infomoney, 7 de outubro de 2008
- ↑ IMPACTO DE LONGO PRAZO DE REFORMAS NA PREVIDÊNCIA UTILIZANDO UM MODELO DE GERAÇÕES SOBREPOSTAS, acesso em 19 de abril de 2019.
- ↑ A Taxa de Juros Natural e a Regra de Taylor no Brasil: 2003-2015, acesso em 19 de abril de 2019.




















![{\displaystyle J=V_{p}[(1+j)^{n}-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33cd2d4f5b7ab47347245c5db1a560d5d3496fad)














































