Teoria das filas

A teoria das filas é um ramo da probabilidade que estuda a formação de filas, através de análises matemáticas precisas e propriedades mensuráveis das filas. Ela provê modelos para demonstrar previamente o comportamento de um sistema que ofereça serviços cuja demanda cresce aleatoriamente, tornando possível dimensioná-lo de forma a satisfazer os clientes e ser viável economicamente para o provedor do serviço, evitando desperdícios e gargalos.
Definições[editar | editar código-fonte]

- Rede de filas - Conjunto de entidades interligadas que oferecem serviços (centros de serviço) e de usuários (clientes).
- Centro de serviço - Representa os recursos do sistema, compreendendo um ou mais servidores e um conjunto de clientes que esperam pelo serviço.
- Fila - Representa os clientes que estão esperando pelo serviço, juntamente com os que estão sendo atendidos pelos servidores.
- Fila de espera - Somente os clientes que estão aguardando pelo serviço.
Sistema de filas[editar | editar código-fonte]
Uma fila ocorre sempre que a procura por um determinado serviço é maior que a capacidade do sistema de prover este serviço.
Um sistema de filas pode ser definido como clientes chegando, esperando pelo serviço (se não forem atendidos imediatamente) e saindo do sistema após terem sido atendidos. "Cliente", em teoria das filas, é um termo genérico, aplicando-se não somente a seres humanos. O conceito pode abranger, por exemplo, processos esperando para receber a CPU; pacotes que chegam a um roteador para serem encaminhados; pessoas esperando no caixa do supermercado, etc.
Aplicações[editar | editar código-fonte]
Existem diversas aplicações da teoria das filas, que podem ser encontradas na literatura de probabilidade, pesquisa operacional e engenharia industrial. Entre elas destacam-se:
- Fluxo de tráfego (aviões, carros, pessoas, comunicações)
- Escalonamento (pacientes em hospitais, programas em computadores)
- Prestação de serviços (bancos, correios, lanchonetes)
Componentes de um sistema de filas[editar | editar código-fonte]
Um sistema de filas consiste no processo de chegada, da distribuição do tempo de serviço, do número de servidores, da capacidade do sistema, da população de usuários e da disciplina de atendimento.
Processo de chegada[editar | editar código-fonte]
O processo de chegada indica qual o padrão de chegada dos clientes no sistema. Apresenta comportamento estocástico, ou seja, as chegadas ocorrem no tempo e no espaço de acordo com as leis da probabilidade; assim, é preciso conhecer qual a distribuição de probabilidade que descreve os tempos entre as chegadas dos clientes.
A distribuição mais comum é a de Poisson, ou seja, os tempos entre as chegadas são exponencialmente distribuídos. Entre outras distribuições, estão a de Erlang, hiperexponencial e arbitrária.
Clientes podem chegar simultaneamente (chegada em batch). Se for possível, é necessário também saber a distribuição de probabilidade do tamanho do batch. A reação do cliente na fila pode variar. Ele pode esperar independentemente do tamanho da fila, também pode decidir não entrar no sistema caso a fila esteja muito grande (cliente decepcionado), ele pode esperar na fila mas depois de um tempo desistir e sair do sistema, e também pode mudar de uma fila para outra em sistemas com servidores paralelos.
O padrão de chegada de clientes em função do tempo pode ser permanente; nesse caso o padrão não muda no tempo, ou seja, a distribuição de probabilidade que descreve as chegadas é independente do tempo. Também pode não ser permanente, isto é, o padrão de chegada muda com o tempo. Por exemplo, a chegada de clientes diminui no horário de almoço.
Distribuição do tempo de serviço[editar | editar código-fonte]
Assim como no processo de chegada, também é necessário conhecer a distribuição de probabilidade do tempo de serviço, sendo válidas as mesmas distribuições apresentadas.
Os serviços podem também ser simples ou batch.
O estado pode ser independente: o processo de atendimento não depende do número de clientes esperando pelo serviço. Em contrapartida, em um estado dependente, o processo de atendimento muda de acordo com o número de clientes na fila. Por exemplo, um servidor pode trabalhar mais rápido quando a fila aumenta ou, ao contrário, ficar confuso e então mais lento.
Da mesma forma que no processo de chegada, o padrão de serviço pode variar de acordo com o tempo. Por exemplo, a experiência adquirida com o serviço pode aumentar a produtividade; o cansaço, por outro lado, pode diminuí-la. Caso não haja variação o padrão é estacionário.


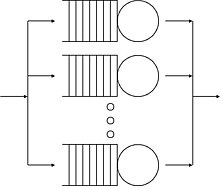
Capacidade do sistema[editar | editar código-fonte]
Representa o número máximo de clientes que o sistema suporta, incluindo os que estão em espera e os que estão sendo atendidos. A capacidade pode ser infinita (mais fácil de analisar) ou finita (por exemplo, número limitado de buffers em um roteador). Se a capacidade for finita, quando o sistema estiver lotado nenhum cliente pode entrar até que um cliente saia do sistema, liberando espaço.
População de usuários[editar | editar código-fonte]
Esse componente indica o número potencial de clientes que podem chegar a um sistema. Pode ser finita ou infinita.
Disciplina de atendimento[editar | editar código-fonte]

Descreve a forma como os clientes saem da fila de espera para serem atendidos. Algumas disciplinas são:
- FIFO (First In, First Out): Primeiro a Entrar, Primeiro a Sair). Disciplina mais comum, inclusive na vida diária. [FIFO também é chamado[1] de FCFS (First Come, First Served): Primeiro a Chegar, Primeiro a ser Atendido.]
- LIFO (Last In, First Out): Último a Chegar, Primeiro a Sair. Aplicável em sistemas em que o item mais recente é mais fácil de ser recuperado, como por exemplo em sistemas de controle de estoque. [LIFO também é chamado[1] de LCFS (Last Come, First Served): Último a chegar, Primeiro a ser Atendido]
- Fila com prioridade: a cada cliente é atribuída uma prioridade; clientes com maior prioridade têm preferência no atendimento. Pode ser de dois tipos:
- Preemptivo: o cliente com maior prioridade é atendido imediatamente, interrompendo o atendimento ao cliente com menor prioridade. Ao terminar, o cliente de menor prioridade volta a ser atendido, podendo continuar o processo de onde parou ou então reiniciá-lo
- Não-preemptivo: o cliente com maior prioridade é colocado no início da fila, recebendo o serviço somente quando o cliente em atendimento sai do sistema, mesmo se este for de prioridade mais baixa
- Round-robin (algoritmo): cada cliente recebe uma fatia de tempo do servidor (quantum), dentro da qual é atendido. Após o término do quantum, se a atividade não foi completada, o cliente é retirado e outro passa a ser atendido. Posteriormente, o cliente que foi interrompido retorna ao servidor e continua a sua atividade. É muito comum em escalonamento de processos da CPU.
- SIRO[2] (Serve In Random Order): Atendimento em Ordem Aleatória. Indenpendente de um item ser recente ou estar na fila há mais tempo, as chances de cada um são as mesmas, enfim, a cada momento, um dos itens da fila será selecionado aleatoriamente.
Notação[editar | editar código-fonte]
As seis características apresentadas acima descrevem um sistema de filas. Para simplificar, utiliza-se a notação de Kendall, proposta em 1953, composta por uma série de símbolos da seguinte forma:
A/S/m/K/N/Q
Em que:
- A: Distribuição dos tempos entre as chegadas (Processo de chegada)
- S: Distribuição dos tempos de serviço
- m: Número de servidores
- K: Capacidade do sistema
- N: Tamanho da população
- Q: Disciplina de atendimento
Exemplos de sistemas de filas[editar | editar código-fonte]
- M/G/4/50/2000/LCFS
- Processo de chegada exponencial (Markoviano) ou de Poisson
- Distribuição dos tempos de serviço arbitrária (Geral)
- Quatro servidores
- Capacidade para cinquenta clientes
- População de dois mil clientes
- Disciplina de atendimento "Último a Chegar, Primeiro a ser Servido"
- D/M/1///RR
- Processo de chegada determinístico
- Distribuição dos tempos de serviço exponencial (Markoviano) ou de Poisson
- Um servidor
- Capacidade ilimitada
- População infinita
- Disciplina de atendimento Round-robin
Muitas vezes, os três últimos símbolos são omitidos. Nestes casos, assume-se capacidade ilimitada, população infinita e disciplina de atendimento FCFS.
Exemplo:
Distribuições de probabilidade[editar | editar código-fonte]
- Exponencial (M)
- Uniforme (U)
- Arbitrária ou Geral (G)
- Erlang ()
- Hiperexponencial ()
Leis operacionais[editar | editar código-fonte]
São relações simples que não necessitam de nenhuma hipótese sobre as distribuições dos tempos de serviço ou dos intervalos entre chegadas. Foram identificadas inicialmente por Buzen em 1976 e posteriormente estendidas por Denning e Buzen em 1978.
Quantidades operacionais[editar | editar código-fonte]
São quantidades que podem ser medidas diretamente durante um período finito de observação.
- Período de observação:
- Número de chegadas (arrivals):
- Número de términos (completions):
- Tempo ocupado (busy time):
- Taxa de chegada:
- Vazão (throughput):
- Utilização:
- Tempo médio de serviço:
Essas quantidades são variáveis que podem mudar de um período de observação para outro. As relações, porém, continuam válidas.
Lei da Utilização[editar | editar código-fonte]
Lei de Little[editar | editar código-fonte]
Desenvolvida por John Little no início dos anos 60, A Lei de Little relaciona o número de clientes no sistema com o tempo médio despendido no sistema.
- Número médio de clientes = Taxa de chegada
xTempo médio de resposta -
- Tempo médio de resposta = Tempo médio de serviço + Tempo médio de espera
A Lei de Little se aplica sempre que o número de chegadas é igual ao número de saídas (denominado sistema em equilíbrio). Pode ser aplicada também em subsistemas (caixa preta).
Se o sistema está em equilíbrio, a taxa de chegada é igual ao throughput, portanto:
Lei do Fluxo Forçado[editar | editar código-fonte]
Relaciona o throughput global do sistema com o throughput dos dispositivos individuais.
Seja o número médio de visitas ao recurso i por uma tarefa. Cada pedido que termina precisa passar, em média, vezes pelo recurso i. Se X pedidos forem concluídos por unidade de tempo, então pedidos terão passado pelo recurso i:
Esta lei é aplicável sempre qua a hipótese do sistema em equilíbrio for verdadeira.
Lei da Demanda de Serviço[editar | editar código-fonte]
Combinando as leis da Utilização e do Fluxo Forçado, obtém-se:
ou
onde é a demanda total de serviço no i-ésimo dispositivo.
O dispositivo com a maior demanda de serviço tem a maior utilização, podendo tornar-se um gargalo no sistema.
Lei Geral do Tempo de Resposta[editar | editar código-fonte]
Sistemas de tempo compartilhado podem ser divididos em dois subsistemas: subsistema de terminais e subsistema de central de processamento. Dados os comprimentos individuais das filas de cada terminal, pode-se determinar :
Dividindo ambos os lados por X e aplicando a Lei do Fluxo Forçado:
ou
Lei do Tempo de Resposta Interativo[editar | editar código-fonte]
Em um sistema interativo, usuários geram pedidos que são processados por um subsistema central e os resultados são devolvidos ao terminal. Entre cada pedido de um usuário, há um tempo ocioso Z.
Aplicando-se a Lei de Little ao subsistema central, tem-se:
Aplicando-a aos M terminais:
Considerando que um cliente ou está sendo atendido ou está ocioso:
Referências
- ↑ a b «Introduction to Queuing». staff.um.edu.mt. Consultado em 22 de agosto de 2019
- ↑ «Queue Structure». Business Jargons (em inglês). 30 de dezembro de 2015. Consultado em 22 de agosto de 2019
Bibliografia[editar | editar código-fonte]
Professores da Universidade Federal do Maranhão:
- Dr. José de Ribamar Braga Pinheiro Júnior
- Dr. Mário Antonio Meireles Teixeira
































