Passeio aleatório



Um passeio aleatório é um objeto matemático que descreve um caminho que consiste de uma sucessão de passos aleatórios. Por exemplo, o caminho traçado por uma molécula conforme ela viaja em um líquido ou um gás, o caminho de um animal buscando alimento, comportamento de supercordas, o preço flutuante de ações e da situação financeira de um jogador pode ser aproximada por modelos de passeio aleatório, mesmo que eles possam não ser verdadeiramente aleatórios na realidade. Como ilustrado por esses exemplos, passeios aleatórios têm aplicações em muitas áreas científicas, incluindo ecologia, psicologia, ciência da computação, física, química, e biologia, e também para a economia. Os passeios aleatórios explicam os comportamentos observados em muitos processos desses campos, e, assim, serve como um modelo fundamental para o registro de atividades estocásticas. Como um aplicação matemática, o valor de pi pode ser aproximado pela utilização de passeios aleatórios no ambiente de modelagem.[1][2] O termo passeio aleatório foi introduzido pela primeira vez por Karl Pearson , em 1905.[3]
Vários tipos diferentes de passeios aleatórios são de interesse, que podem diferir em vários aspectos. O próprio termo geralmente se refere a uma categoria especial de cadeias de Markov ou processos de Markov, mas muitos processos dependentes do tempo são referidos como passeios aleatórios, com um modificador que indica suas propriedades específicas. Passeios aleatórios (de Markov ou não) também podem acontecer em uma variedade de espaços: os mais comumente estudados incluem gráficos, outros entre os números inteiros ou reais, no plano ou em espaços vetoriais de dimensões superiores, em superfícies curvas ou em dimensões superiores de campo riemaniano, e também em grupos finitos, finitamente gerados ou grupo de Lie. O parâmetro de tempo também pode ser alterado. No contexto mais simples, a caminhada é em tempo discreto, que é uma sequência de variáveis aleatórias indexadas pelos números naturais. No entanto, também é possível definir passeios aleatórios que levam seus passos em momentos aleatórios, e, nesse caso, a posição tem de ser definido para todos os tempos . Casos específicos ou limites de passeios aleatórios incluem voos de Lévy e modelos de difusão, tais como o movimento Browniano.
Passeios aleatórios são um tema fundamental na discussão de processos de Markov. O estudo matemático deles tem sido intenso. Várias propriedades, incluindo, mas não limitado a distribuições de dispersão, tempo de retorno, taxas de encontro, recorrência ou transitoriedade, foram introduzidas para quantificar o seu comportamento.
Definição[editar | editar código-fonte]
O passeio aleatório mais simples é um caminho construído de acordo as seguintes regras:
- Há um ponto de partida.
- A distância de um ponto no caminho até o próximo é constante.
- A direção de um ponto no caminho para o próximo é escolhido aleatoriamente, e nenhuma direção é mais provável do que outra.
Passeio aleatório em malha[editar | editar código-fonte]
Um modelo de passeio aleatório popular é o passeio aleatório em uma estrutura regular, onde a cada passo a localização salta para outro local de acordo com alguma distribuição de probabilidade. Em um passeio aleatório simples, a localização só pode saltar para locais vizinhos da rede, formando um caminho de rede. No passeio aleatório simétrico simples em uma rede localmente finita, as probabilidades do salto de localização para cada um de seus vizinhos imediatos são as mesmas. O melhor exemplo estudado é de passeio aleatório sobre o inteiro rede d-dimensional (às vezes chamado de treliça hipercúbica) .[4]
Passeio aleatório unidimensional[editar | editar código-fonte]
Um exemplo elementar de um passeio aleatório é o passeio aleatório na linha de número inteiro, , que começa em 0 e em cada etapa move +1 ou -1 com igual probabilidade.
Este percurso pode ser ilustrado como se segue. Um marcador é colocado no zero na linha de número e uma moeda honesta é lançada. Se der cara, o marcador é movido uma unidade para a direita. Se der coroa, o marcador é movido uma unidade para a esquerda. Após cinco jogos, o marcador pode agora estar em 1, -1, 3, -3, 5, ou -5. Com cinco lançamentos, três caras e duas coroas, em qualquer ordem, vai terminar em 1. Há 10 maneiras de resultar em 1 (lançando três caras e duas coroas), 10 maneiras de resultar em -1 (lançando três coroas e duas caras), 5 formas de resultar em 3 (lançando quatro caras e uma coroa), 5 formas de resultar em -3 (lançando quatro coroas e uma cara), uma forma de resultar em 5 (lançando cinco caras), e uma forma de resultar em -5 (lançando cinco coroas). Veja abaixo uma ilustração dos resultados possíveis de 5 lançamentos.



Para definir esta caminhada formalmente, toma-se variáveis aleatórias independentes , onde cada variável é +1 ou −1, com uma probabilidade de 50% para qualquer valor, e definir e . A série é chamada passeio aleatório simples em . Esta série (a soma da seqüência de −1 e +1) dá a distância percorrida, se cada parte do passeio é de comprimento 1. A expectativa de é zero. Isto é, a média de todos os lançamentos se aproxima de zero conforme o número de lançamentos aumenta. Isto segue pela propriedade da aditividade finita da expectativa:
Um cálculo semelhante, utilizando a independência de variáveis aleatórias e o fato de que , mostra que:
Isto sugere que , a distância esperada depois de n passos, deve ser da ordem de . De fato,[5]
Este resultado mostra que a difusão é ineficaz para a mistura devido à forma como a raiz quadrada funciona para grandes .
Quantas vezes um passeio aleatório atravessa uma linha de fronteira se for permitido continuar a caminhar para sempre? Um passeio aleatório simples em vai atravessar cada ponto um número infinito de vezes. Este resultado tem muitos nomes: o fenômeno da passagem de nível, recorrência ou o ruína do jogador. A razão para o último nome é o seguinte: um jogador com uma quantidade finita de dinheiro vai eventualmente perder ao jogar um jogo justo contra uma banca com uma quantidade infinita de dinheiro. O dinheiro do jogador irá realizar um passeio aleatório, e ele vai chegar a zero em algum ponto, e o jogo irá acabar.
Se a e b são números inteiros positivos, então o número esperado de passos até que um passeio aleatório unidimensional simples começando em 0 primeiro atingir b ou −a é ab. A probabilidade de que este passeio vai atingir b antes de −a é que pode ser derivado do fato de que o passeio aleatório simples é um martingale.
Alguns dos resultados mencionados acima podem ser derivados a partir de propriedades do triângulo de Pascal. O número de diferentes passeios de n passos, onde cada passo é +1 ou −1 é 2n. Para um passeio aleatório simples, cada um desses passeios são igualmente prováveis. Para que Sn ser igual a um número k , é necessário e suficiente que o número de passos +1 no passeio exceda o de −1 por k. O número de passeios que satisfazem é igual ao número de maneiras de escolher (n - k)/2, com n sendo o número de movimentos permitidos,[6] denotado . Para que isto tenha sentido, é necessário que n e k sejam números pares. Portanto, a probabilidade de que é igual a . Representando as entradas do triângulo de Pascal, em termos de fatoriais e usando a fórmula de Stirling, pode-se obter boas estimativas para estas probabilidades para valores grandes de .
Se o espaço é limitado para + para ser breve, o número de maneiras em que um passeio aleatório vai pousar em qualquer determinado número tendo ocorrido cinco lançamentos, pode ser mostrado como {0,5,0,4,0,1}.
Esta relação com o triângulo de Pascal é demonstrada para valores pequenos de n. Com zero lançamentos, a única possibilidade será a de permanecer em zero. No entanto, com um lançamento, há uma chance de resultar em −1, ou uma chance de resultar em 1. Com dois lançamentos, um marcador em 1 pode mover para 2 ou voltar para zero. Um marcador em −1, poderia mover para −2 ou de volta a zero. Portanto, há uma chance de resultar em −2, duas chances de terminar em zero, e uma chance de pouso em 2.
| k | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||||
| 1 | 1 | ||||||||||
| 1 | 2 | 1 | |||||||||
| 1 | 3 | 3 | 1 | ||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||
| 1 | 5 | 10 | 10 | 5 | 1 |
O teorema do limite central e a lei do logaritmo iterado descreve aspectos importantes do comportamento de passeios aleatórios simples em . Em particular, o primeiro implica que conforme n aumenta, as probabilidades (proporcional aos números em cada linha) se aproximam de uma distribuição normal.
Como uma generalização direta, pode-se considerar passeios aleatórios em reticulados (infinitas vezes cobrindo gráficos ao longo do finito gráficos). Na verdade, é possível estabelecer o teorema do limite central nesta definição.[7][8]
Cadeia de Markov[editar | editar código-fonte]
Um passeio aleatório unidimensional também pode ser visto como uma cadeia de Markov cujo espaço de estado é dado por números inteiros . Para algum número p satisfazendo , as probabilidades de transição (a probabilidade Pi,j de ocorrer um movimento a partir do estado i para o estado j) são dadas por .
Dimensões superiores[editar | editar código-fonte]
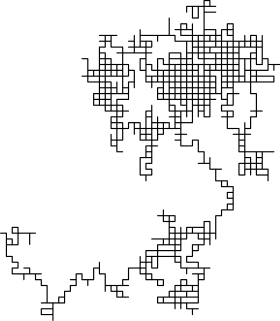
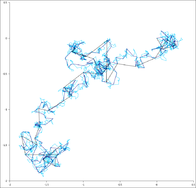
Em dimensões superiores, o conjunto de pontos caminhados aleatoriamente tem interessantes propriedades geométricas. Na verdade, obtém-se um fractal discreto, isto é, um conjunto que apresenta autossimilaridade estocástica em grandes escalas. Em escalas pequenas, pode-se observar a "irregularidade" resultante da grade em que o caminho é realizado. A trajetória de um passeio aleatório é o conjunto dos pontos visitados, considerado como um todo e ignorando quando o passeio chegou a cada ponto. Em uma dimensão, a trajetória é simplesmente todos os pontos entre a altura mínima e máxima que o caminho alcançou (ambos são, em média, na ordem de √n).
Para visualizar os casos de duas dimensões, pode-se imaginar uma pessoa andando aleatoriamente em torno de uma cidade. A cidade é efetivamente infinita e com calçadas dispostas em uma grade quadrada. Em cada cruzamento, a pessoa escolhe aleatoriamente uma das quatro rotas possíveis (incluindo a rota pela qual veio até aquele ponto). Formalmente, este é um passeio aleatório no conjunto de todos os pontos do plano com coordenadas nos inteiros.
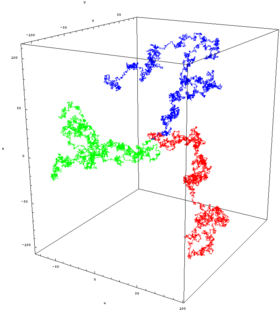
Será que a pessoa voltará em algum momento ao ponto de partida original do passeio? Este é o equivalente bidimensional da passagem de nível, discutida acima. A pessoa quase certamente irá voltar ao ponto de partida em um passeio aleatório bidimensional, mas para 3 dimensões ou mais, a probabilidade de retorno à origem diminui à medida que o número de dimensões aumenta. Em 3 dimensões, a probabilidade diminui para cerca de 34%.[9]
Processo de Wiener[editar | editar código-fonte]
Um processo de Wiener é um processo estocástico com comportamento semelhante ao movimento Browniano, o fenômeno físico de partículas minúsculas difundindo em um fluido (às vezes, o processo de Wiener é chamado de "movimento Browniano", embora esse seja, estritamente falando, uma confusão de um modelo com o fenômeno a ser modelado).
Um processo de Wiener é a escala limite de passeio aleatório em uma dimensão. Isso significa que, se você tomar um passeio aleatório com passos muito pequenos, você obtém uma aproximação para um processo de Wiener (e, menos precisamente, para um movimento Browniano). Para ser mais preciso, se o tamanho do passo é ε, é preciso ter uma caminhada de comprimento L/ε2 para se aproximar de um Wiener de comprimento L. Conforme o tamanho do passo tende a 0 (e o número de passos aumenta proporcionalmente), os passeios aleatórios convergem para um processo de Wiener. Formalmente, se B é o espaço de todos os caminhos de comprimento L , com a topologia máxima, e se M é o espaço de medida através de B com a topologia normal, então a convergência se dá no espaço M. Da mesma forma, um processo de Wiener em várias dimensões é a escala limite de passeios aleatórios no mesmo número de dimensões.
Um passeio aleatório é um fractal discreto (uma função com número inteiro dimensões; 1, 2, ...), mas a trajetória de um processo de Wiener é um verdadeiro fractal, e há uma conexão entre os dois. Por exemplo, tome um passeio aleatório até que ele atinja um círculo de raio r vezes o comprimento do passo. A média do número de passos que ele executa é r2. Essa é a versão discreta do caminho de um processo de Wiener ser um fractal de dimensão Hausdorff 2.
Em duas dimensões, o número médio de pontos que o mesmo passeio aleatório tem no limite de sua trajetória é de r4/3. Isto corresponde ao fato de que o limite da trajetória de um processo de Wiener é um fractal de dimensão 4/3, um fato previsto por Mandelbrot usando simulações, mas provado apenas em 2000 por Lawler, Schramm e Werner.[10]
Um processo de Wiener possui muitas simetrias que passeio aleatório não tem. Por exemplo, um passeio em processo de Wiener é invariante à rotação, mas o passeio aleatório não, pois a grade subjacente não é invariante (passeios aleatórios são invariantes para as rotações de 90 graus, mas processos de Wiener são invariantes para rotações, por exemplo, de 17 graus). Isso significa que, em muitos casos, problemas de passeio aleatório são mais fáceis de resolver "traduzindo-os" para um processo de Wiener, resolvendo o problema e, em seguida, transformando de volta. Por outro lado, alguns problemas são mais fáceis de resolver com passeios aleatórios, devido à sua natureza discreta.
Passeios aleatórios e processos de Wiener podem ser acoplados, se manifestando sobre o mesmo espaço de probabilidade de forma dependente que os obriga a estar muito próximos. O mais simples de tais acoplamento é o acoplamento de Skorokhod, mas existem acoplamentos mais precisos, tais como o teorema de aproximação de Komlós–Grande–Tusnády.
A convergência de um passeio aleatório em direção a um processo de Wiener é controlada pelo teorema central do limite, e pelo teorema de Donsker. Para uma partícula em uma conhecida posição fixa em t = 0, o teorema central do limite diz que depois de um grande número de passos independentes no passeio aleatório, a posição do caminhante é distribuída de acordo com uma distribuição normal do total de variância:
onde t é o tempo decorrido desde o início do passeio aleatório, é o tamanho de um passo do passeio aleatório, e é o tempo decorrido entre dois passos sucessivos.
Isso corresponde à função de Green da equação de difusão que controla o processo de Wiener, o que sugere que, depois de um grande número de passos, o passeio aleatório converge em direção a um processo de Wiener.
Em 3D, a variância correspondente à função de Green de difusão da equação é:
Ao equalizar essa quantidade com a variância associada à posição do caminhante aleatório, obtém-se o coeficiente de difusão equivalente a ser considerado para o processo de Wiener para qual o passeio aleatório converge depois de um grande número de passos:
- (válido apenas em 3D)
Observação: as duas expressões da variância acima correspondem à distribuição associada ao vetor que liga as duas extremidades do passeio aleatório, em 3D. A variância associada a cada componente , ou é apenas um terço deste valor (em 3D).
Para 2D:[11]
E para 1D:[12]
Passeio aleatório gaussiano[editar | editar código-fonte]
Um passeio aleatório com um passo de tamanho que varia de acordo com uma distribuição normal é usado como um modelo para séries de dados temporais do mundo real, tais como os mercados financeiros. A fórmula de Black–Scholes para a modelagem de opção de preços, por exemplo, usa um passeio aleatório gaussiano como a suposição subjacente.
Aqui, o tamanho do passo é o inverso da distribuição cumulativa normal onde 0 ≤ z ≤ 1 é uma distribuição uniforme de números aleatórios, e μ e σ são a média e o desvio-padrão da distribuição normal, respectivamente.
Se μ é diferente de zero, o passeio aleatório irá variar sobre uma tendência linear. Se vs é o valor inicial do passeio aleatório, o valor esperado depois de n passos será vs + nμ.
Para o caso especial onde μ é igual a zero, depois de n passos, a distância de translação da distribuição de probabilidade é dada por N(0, nσ2), onde N(a) é a notação para a distribuição normal, n é o número de passos, e σ é dado a partir da distribuição normal cumulativa inversa conforme indicado acima.
Prova: O passeio aleatório gaussiano pode ser considerado como a soma de uma série de independentes e identicamente distribuídas variáveis aleatórias Xi, do inverso da distribuição cumulativa normal com média igual a zero e σ da distribuição normal cumulativa inversa original:
- Z = ,
mas tem-se a distribuição para a soma de duas variáveis aleatórias independentes e normalmente distribuídas, Z = X + Y, é dada por
- N(μX + μY, σ2X + σ2Y)
No caso, µX = µY = 0 e σ2X = σ2Y = σ2 resultando em
- N(0, 2σ2)
Por indução, para n passos tem-se
- Z ~ N(0, nσ2).
Para as etapas distribuídas de acordo com qualquer distribuição, com zero de média e uma variância finita (não necessariamente apenas uma distribuição normal), o valor eficaz da distância da tradução depois de n passos é
Mas para o passeio aleatório gaussiano, este é apenas o desvio padrão da distância da tradução da distribuição depois de n passos. Portanto, se μ é igual a zero, e por que o valor eficaz (rms) da distância da tradução é um desvio-padrão, há 68.27% de probabilidade de que o rms da distância da tradução depois de n passos vai cair entre ± σ. Da mesma forma, há 50% de probabilidade de que a distância da tradução depois de n passos vai cair entre ± σ 0.6745.
Difusão anômala[editar | editar código-fonte]
Em sistemas desordenados como meios porosos e fractais pode não ser proporcional a mas a . O expoente é chamado expoente de difusão anômala e pode ser maior ou menor do que 2.[13] A difusão anômala também pode ser expressa como σr2 ~ Dtα , onde α é o parâmetro de anomalia. Algumas difusões em ambientes aleatórios são proporcionais a uma potência do logaritmo do tempo. Ver, por exemplo, passeio do Sinai ou difusão Brox.
Número de sítios distintos[editar | editar código-fonte]
O número de diferentes sítios visitados por um único caminhante aleatório tem sido extensivamente estudado para redes quadradas e cúbicas, e para fractais.[14][15] Esta quantidade é útil para a análise de problemas de reações cinéticas. Também está relacionado com a densidade de estados vibracionais,[16][17] a processos de reações de difusão [18] e a disseminação de populações em ecologia.[19] A generalização deste problema para o número de sítios distintos visitados pelos caminhantes aleatórios, recentemente foram estudadas para o binomial euclidiano d-dimensional.[20] O número de diferentes sítios visitados por N caminhantes não está simplesmente relacionada com o número de diferentes sítios visitados por cada caminhante.
Aplicações[editar | editar código-fonte]

Como mencionado, a gama de fenômenos naturais que têm sido alvo de tentativas de descrição como tipos de passeios aleatórios é considerável, em particular, na física[21][22] e na química,[23] em ciência dos materiais,[24][25] na biologia[26] e em vários outros campos.[27][28] A seguir estão algumas aplicações específicas de passeios aleatórios:
- Em economia financeira, a "hipótese do passeio aleatório" é usada para modelar preços de ações e de outros fatores. Estudos empíricos encontraram alguns desvios a partir deste modelo teórico, especialmente nas correlações de curto e longo prazo correlações.
- Em genética populacional, passeios aleatórios descrevem as propriedades estatísticas de deriva genética.
- Na física, passeios aleatório são usados como modelos simplificados de movimentos Brownianos e difusão físicos, tais como o movimento aleatório de moléculas em líquidos e gases. Veja, por exemplo, a difusão limitada. Também em física, passeios aleatórios e alguns dos passeios autointeragentes desempenham um papel na teoria quântica de campos.
- Em ecologia matemática, passeios aleatórios são usados para descrever movimentos de animais individuais, para empiricamente apoiar os processos de biodifusão, e, ocasionalmente, para modelar dinâmicas de populações.
- Em física de polímeros, um passeio aleatório descreve uma cadeia ideal. É o modelo mais simples para o estudo de polímeros.
- Em outros campos da matemática, o passeio aleatório é usado para calcular soluções para a equação de Laplace, para estimar a medida harmônica, e por várias construções em análise e combinatória.
- Em ciência da computação, passeios aleatórios são usados para estimar o tamanho da Web. Na conferência da World Wide Web de 2006, Bar-Yossef et al. publicou os seus resultados e algoritmos para o mesmo.
- Na segmentação de imagens, passeios aleatórios são usados para determinar as etiquetas (por exemplo, "objeto" ou "fundo") para associar cada pixel.[29] Este algoritmo é normalmente referido como o algoritmo de segmentação do caminhante aleatório.
Em todos estes casos, o passeio aleatório é frequentemente substituído por um movimento Browniano.
- Na pesquisa do cérebro, passeios aleatórios e passeios aleatórios reforçados são usados para modelar cascatas de disparo de neurônios no cérebro.
- Na visão, a deriva ocular tende a se comportar como um passeio aleatório.[30] De acordo com alguns autores, movimentos fixacionais dos olhos em geral também são bem descritos por passeios aleatórios.[31]
- Em psicologia, passeios aleatórios explicam com precisão a relação entre o tempo necessário para tomar uma decisão e a probabilidade de que uma determinada decisão seja tomada.[32]
- Passeios aleatórios podem ser usados para amostrar um espaço de estado que é desconhecido ou muito grande, por exemplo, escolher uma página aleatória da internet ou, para a investigação das condições de trabalho de um trabalhador ao acaso em um determinado país.
- Quando esta última abordagem é usada em ciência da computação é conhecido como Cadeia de Markov de Monte Carlo ou MCMC. Muitas vezes, a amostragem de alguns espaços de estado complicados também permite obter uma estimativa probabilística do tamanho do espaço. A estimativa do permanente de uma grande matriz de zeros e uns foi o primeiro grande problema a ser resolvido usando esta abordagem.
- Passeios aleatórios também têm sido utilizados como exemplo de gráficos online massivos, tais como de redes sociais online.
- Em redes sem fio, um passeio aleatório é usado para modelar o movimento através dos nós.
- Bactérias móveis utilizam um passeio aleatório tendencioso.
- Passeios aleatórios são utilizados para modelar jogos de azar.
- Em física, passeios aleatórios fundamentam o método da estimativa de Fermi.
- Na web, o site do Twitter utiliza passeios aleatórios para fazer sugestões de quem seguir.[33]
- Dave Bayer e Persi Diaconis provaram que 7 movimentos são o suficiente para embaralhar um deck de cartas. Este resultado se traduz em uma declaração sobre o passeio aleatório no grupo simétrico que é o que eles provam, com um crucial uso da estrutura do grupo via análise de Fourier.
Variantes de passeios aleatórios[editar | editar código-fonte]
Um número de tipos de processos estocásticos têm sido considerados, que são semelhantes aos passeios aleatórios "puros", mas onde a estrutura simples é permitida ser mais generalizada. A estrutura "pura" pode ser caracterizada pelos passos a serem definidas pelas variáveis aleatórias independentes e identicamente distribuídas.
Passeio aleatório em grafos[editar | editar código-fonte]
Um passeio aleatório de comprimento k em um possivelmente infinito grafo G com uma raiz 0 é um processo estocástico com variáveis aleatórias de tal forma que e é um vértice escolhido uniformemente ao acaso a partir dos vizinhos de . Então, o número é a probabilidade de que um passeio aleatório de comprimento k começando em v, termina em w. Em particular, se G é um grafo com raiz 0, é a probabilidade de que um passeio aleatório de passo retorna a 0.
Suponha agora que a cidade não é mais um grade quadrada perfeita. Quando o caminhante chega a um determinado cruzamento, ele escolhe entre os vários disponíveis caminhos com igual probabilidade. Assim, se o cruzamento tem sete saídas, o caminhante vai para cada uma com probabilidade de um sétimo. Este é um passeio aleatório em um gráfico. É possível, sob certas condições, o caminhante retornar a sua casa. Por exemplo, se os comprimentos de todos os blocos que estão entre a e b (onde a e b são quaisquer dois números positivos finitos) então o caminhante vai, quase certamente, chegar a sua casa. Observe que não se assume que o grafo é planar, por exemplo, a cidade pode conter túneis e pontes. Uma maneira de provar este resultado é usando a conexão das redes elétricas. Pegue um mapa da cidade e coloque um resistor de um ohm em cada bloco. Agora, meça a "resistência entre um ponto e o infinito". Em outras palavras, escolha algum número R e tome todos os pontos da rede elétrica com distância maior do que R a partir do ponto de partida, conectando-os. Esta é agora uma rede elétrica finita e podemos medir a resistência do ponto de partida as pontos cabeados. Leve R para o infinito. O limite é chamado de resistência entre um ponto e o infinito. Acontece que o seguinte é verdadeiro:
Teorema: um grafo é transitivo se, e somente se, a resistência entre o ponto e o infinito é finito. Não é importante que ponto é escolhido se o gráfico está ligado.
Em outras palavras, em um sistema transitório, só precisa superar uma resistência finita para chegar ao infinito a partir de qualquer ponto. Em um sistema recorrente, a resistência a partir de qualquer ponto até o infinito é infinito.
Esta caracterização da reincidência e da transitoriedade permite analisar o caso de uma cidade desenhada no plano com as distâncias limitadas.
Um passeio aleatório em um grafo é um caso muito especial de uma cadeia de Markov. Ao contrário de uma cadeia de Markov geral, o passeio aleatório em um grafo possui uma propriedade chamada de simetria de tempo ou reversibilidade. Grosseiramente falando, esta propriedade, também chamada de princípio do equilíbrio detalhado, significa que as probabilidades para atravessar um determinado caminho em um sentido ou no outro, têm uma forma muito simples de ligação entre elas (se o gráfico é normal, elas são somente iguais). Esta propriedade tem conseqüências importantes.
Começando na década de 1980, muita investigação tem ido para ligar propriedades do grafo ao passeio aleatório. Além das conexões da rede elétrica descritas acima, existem conexões importantes para as desigualdades isoperimétrica, desigualdades funcionais, tais como as desigualdades de Sobolev e Poincaré e propriedades de soluções de equação de Laplace. Uma parte significativa desta pesquisa foi focada em grafos de Cayley de grupos finitamente gerados. Em muitos casos, estes resultados discretos persistem, ou são derivados a partir de coletores e de grupos de Lie.
No contexto de grafos aleatórios e, particularmente, do modelo Erdős–Rényi, os resultados analíticos para algumas propriedades de caminhantes aleatórios foram obtidos. Estes incluem a distribuição do primeiro[34] e o último tempo de passada[35] do caminhante, onde o primeiro tempo é dado pela primeira vez que o caminhante passa em um sítio visitado anteriormente do grafo, e o último tempo de passada corresponde a primeira vez que o caminhante não pode executar um movimento adicional sem revisitar um sítio visitado anteriormente.
Uma boa referência para o passeio aleatório em gráficos é o livro on-line por Aldous e Fill. Para grupos consulte o livro de Woess. Se a transição do kernel é aleatória (baseado em um ambiente de ) então o passeio aleatório é chamado de um "passeio aleatório em ambiente aleatório".
Pode-se pensar sobre a escolha de cada vértice possível com a mesma probabilidade, como a maximização de incerteza (entropia) localmente. Também é possível fazê-lo globalmente – em um passeio aleatório de máxima entropia (MERW) busca-se que todos os caminhos sejam igualmente prováveis, ou em outras palavras: para cada dois vértices, cada caminho de comprimento dado é igualmente provável. Este passeio aleatório tem propriedades de localização muito mais fortes.
Passeio aleatório com auto-interação[editar | editar código-fonte]
Há uma série de modelos interessantes de caminhos aleatórios, em que cada etapa depende do passado de uma maneira específica. Todos são mais complexos para resolver analiticamente que o passeio aleatório habitual; ainda assim, o comportamento de qualquer modelo de um caminhante aleatório pode ser obtido usando computadores. Os exemplos incluem:
- Caminho autoevitante (Madras e Slade, 1996).[36]
O caminho autoevitante de comprimento n em Z^d é o caminho aleatória de n passos que começa na origem, faz transições somente entre locais adjacentes em Z^d, nunca revisita um sítio, e é escolhido uniformemente entre todos esses caminhos. Em duas dimensões, devido ao auto-aprisionamento, um caminho autoevitante típico é bastante curto,[37] enquanto em dimensões superiores, cresce para além de todos os limites. Este modelo tem sido frequentemente utilizado na física de polímeros (desde 1960).
- Passeio aleatório de loop apagado (Gregory Lawler).[38][39]
- Passeio aleatório reforçado (Robin Pemantle 2007).[40]
- Processo de exploração.
- Passeio aleatório multiagente.[41]
Passeios correlacionados de longo alcance[editar | editar código-fonte]
Séries temporais correlacionadas de longo alcance são encontradas em muitos sistemas biológicos, climáticos e econômicos.
- Registros de pulsação.[42]
- Sequências de DNA não-codificado.[43]
- Volatilidade de ações[44]
- Registros de temperatura em todo o mundo.[45]
Passeios em espaços com diferentes dimensões e geometrias[editar | editar código-fonte]
Passeios aleatórios em certos "grupos", que são objetos que podem ter geometrias muito diversas, ela acabará, depois de muito tempo, se unir em uma direção específica. Nesses casos, os passeios são considerados dependentes do caminho, o que implica que algo que ocorreu no início influencia o resultado. De qualquer forma, para grupos diferentes, a trajetória das caminhadas não se misturam e a história deles não afeta o futuro. Alguns matemáticos perguntaram: por um processo aleatório, é verdade que, a longo prazo, tudo se esvai e o que quer que aconteça acontecerá, independentemente do que ocorreu anteriormente? Ou há uma lembrança do que aconteceu antes?[46]
Em passeios aleatórios, existem grupos que possuem essas memórias, enquanto em outros grupos as memórias são apagadas. Para saber quais grupos têm essa propriedade e quais não - ou seja, o que faz um grupo ter memória - a solução é a maneira geométrica de descrever uma propriedade algébrica dos grupos. O problema resolvido estudando a conexão entre as propriedades geométricas e algébricas dos grupos. Para entender a essência disso, pense em um círculo. Você pode descrever o círculo geometricamente (como o conjunto de todos os pontos a uma determinada distância de um ponto) ou pode descrevê-lo com uma equação algébrica.[47]
Ver também[editar | editar código-fonte]
- Movimento browniano
- Lei do logaritmo iterado
- Voos de Lévy
- Hipótese de buscas por voos de Lévy
- Caminho autoevitante
- Raiz unitária
Referências
- ↑ Wirth, E.; Szabó, G.; Czinkóczky, A. (8 de junho de 2016). «MEASURE LANDSCAPE DIVERSITY WITH LOGICAL SCOUT AGENTS». ISPRS - International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences (em English). XLI-B2: 491–495. ISSN 1682-1750. doi:10.5194/isprs-archives-xli-b2-491-2016
- ↑ Wirth E. (2015). Pi from agent border crossings by NetLogo package. Retrieved from Wolfram Library Archive: http://library.wolfram.com/infocenter/MathSource/9281/
- ↑ Pearson, K. (1905). The Problem of the Random Walk. Nature. 72, 294.
- ↑ Révész Pal, Random walk in random and non random environments, World Scientific, 1990
- ↑ [1]
- ↑ Edward A. Colding et al, Random walk models in biology, Journal of the Royal Society Interface, 2008
- ↑ M. Kotani, T. Sunada (2003). «Spectral geometry of crystal lattices». Contemporary. Math. 338: 271–305. doi:10.1090/conm/338/06077
- ↑ M. Kotani, T. Sunada (2006). «Large deviation and the tangent cone at infinity of a crystal lattice». Math. Z. 254: 837–870. doi:10.1007/s00209-006-0951-9
- ↑ Pólya's Random Walk Constants
- ↑ Dana Mackenzie, Taking the Measure of the Wildest Dance on Earth, Science, Vol. 290, no. 5498, pp. 1883–1884.
- ↑ [2]
- ↑ [3]
- ↑ D. Ben-Avraham and S. Havlin, Diffusion and Reactions in Fractals and Disordered Systems, Cambridge University Press, 2000.
- ↑ Weiss, George H.; Rubin, Robert J. (1982).
- ↑ Blumen, A.; Klafter, J.; Zumofen, G. (1986).
- ↑ Alexander, S.; Orbach, R. (1982).
- ↑ Rammal, R.; Toulouse, G. (1983).
- ↑ Smoluchowski, M.V. (1917).
- ↑ Skellam, J. G. (1951).
- ↑ Larralde, Hernan; Trunfio, Paul; Havlin, Shlomo; Stanley, H. Eugene; Weiss, George H. (1992).
- ↑ Risken H., The Fokker–Planck Equation (Springer, Berlin) 1984.
- ↑ De Gennes P. G., Scaling Concepts in Polymer Physics (Cornell University Press, Ithaca and London) 1979.
- ↑ Van Kampen N. G., Stochastic Processes in Physics and Chemistry, revised and enlarged edition (North-Holland, Amsterdam) 1992.
- ↑ Weiss, George H. (1994), Aspects and Applications of the Random Walk, Random Materials and Processes, North-Holland Publishing Co., Amsterdam, ISBN 0-444-81606-2, MR 1280031 .
- ↑ Doi M. and Edwards S. F., The Theory of Polymer Dynamics (Clarendon Press, Oxford) 1986
- ↑ Goel N. W. and Richter-Dyn N., Stochastic Models in Biology (Academic Press, New York) 1974.
- ↑ Redner S., A Guide to First-Passage Process (Cambridge University Press, Cambridge, UK) 2001.
- ↑ Cox D. R., Renewal Theory (Methuen, London) 1962.
- ↑ Leo Grady (2006): "Random Walks for Image Segmentation" Arquivado em 19 de julho de 2011, no Wayback Machine., IEEE Transactions on Pattern Analysis and Machine Intelligence, pp. 1768–1783, Vol. 28, No. 11
- ↑ Rucci, M., Victor, J. D. (2015).
- ↑ Ralf Engbert, Konstantin Mergenthaler, Petra Sinn, and Arkady Pikovsk: "An integrated model of fixational eye movements and microsaccades"
- ↑ «Nosofsky, 1997» (PDF). Consultado em 10 de dezembro de 2004. Arquivado do original (PDF) em 10 de dezembro de 2004
- ↑ Pankaj Gupta, Ashish Goel, Jimmy Lin, Aneesh Sharma, Dong Wang, and Reza Bosagh Zadeh WTF: The who-to-follow system at Twitter, Proceedings of the 22nd international conference on World Wide Web
- ↑ Tishby, Biham, Katzav (2016), The distribution of first hitting times of random walks on Erdős-Rényi networks, arXiv:1606.01560.
- ↑ Tishby, Biham, Katzav (2016), The distribution of path lengths of self avoiding walks on Erdős-Rényi networks, arXiv:1603.06613.
- ↑ Neal Madras and Gordon Slade (1996), The Self-Avoiding Walk, Birkhäuser Boston.
- ↑ S. Hemmer & P. C. Hemmer (1984), "An average self-avoiding random walk on the square lattice lasts 71 steps", J. Chem.
- ↑ Gregory Lawler (1996).
- ↑ Gregory Lawler, Conformally Invariant Processes in the Plane, book.ps.
- ↑ Robin Pemantle (2007), A survey of random processes with reinforcement.
- ↑ Alamgir, M and von Luxburg, U (2010).
- ↑ C.-K. Peng, J. Mietus, J. M. Hausdorff, S. Havlin, H. E. Stanley, A. L. Goldberger (1993).
- ↑ C.-K. Peng, S. V. Buldyrev, A. L. Goldberger, S. Havlin, F. Sciortino, M. Simons, H. E. Stanley (1992).
- ↑ Y. Liu, P. Cizeau, M. Meyer, C.-K. Peng, H. E. Stanley (1997).
- ↑ E. Koscielny-Bunde; A. Bunde; S. Havlin; H. E. Roman; Y. Goldreich; H.-J. Schellenhuber (1998).
- ↑ «Scientists solves a long-standing problem of 'Random Walk' in pure math» (em inglês). 31 de março de 2020
- ↑ Frisch, Joshua; Hartman, Yair; Tamuz, Omer; Vahidi Ferdowsi, Pooya (julho de 2019). «Choquet-Deny groups and the infinite conjugacy class property». Annals of Mathematics. 190: 307–320. ISSN 0003-486X
Leitura adicional[editar | editar código-fonte]
- Aldous, David; Fill, Jim, Reversible Markov Chains and Random Walks on Graphs, https://web.archive.org/web/20040921020230/http://stat-www.berkeley.edu/users/aldous/RWG/book.html
- Ben-Avraham D.; Havlin S., Diffusion and Reactions in Fractals and Disordered Systems, Cambridge University Press, 2000.
- Feller, William (1968), An Introduction to Probability Theory and its Applications (Volume 1). ISBN 0-471-25708-7
- Hughes, Barry D. (1996), Random Walks and Random Environments, Oxford University Press. ISBN 0-19-853789-1
- Mackenzie, Dana, "Taking the Measure of the Wildest Dance on Earth", Science, Vol. 290, 8 December 2000.
- Norris, James (1998), Markov Chains, Cambridge University Press. ISBN 0-521-63396-6
- Pólya G.(1921), "Über eine Aufgabe der Wahrscheinlichkeitsrechnung betreffend die Irrfahrt im Strassennetz", Mathematische Annalen, 84(1-2):149–160, March 1921.
- Révész, Pal (2013), Random Walk in Random and Non-random Environments (Third Edition), World Scientific Pub Co. ISBN 978-981-4447-50-8
- Weiss G. Aspects and Applications of the Random Walk, North-Holland, 1994.
- Woess, Wolfgang (2000), Random Walks on Infinite Graphs and Groups, Cambridge tracts in mathematics 138, Cambridge University Press. ISBN 0-521-55292-3
- Toshikazu Sunada (2012), Topological Crystallography --With a View Towards Discrete Geometric Analysis--, Surveys and Tutorials in the Applied Mathematical Sciences, Vol. 6, Springer
























![{\displaystyle P[S_{0}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4fec1fd8784c3de7c8b113f7ff728db75c8f584)
![{\displaystyle 2P[S_{1}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c61317a7c5e847ee2756e0a746abee7bdd9da12)
![{\displaystyle 2^{2}P[S_{2}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca9583c3e61f6b6739502821af6cb79fae46f22e)
![{\displaystyle 2^{3}P[S_{3}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/283a77c450ba9f63e54a01a94fb9cec8e8ee07b8)
![{\displaystyle 2^{4}P[S_{4}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/208950bbe9ff3b0dd09b94b35dd390d3ddefea15)
![{\displaystyle 2^{5}P[S_{5}=k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b86e6675acd3df11dbd6fd80d3e1c0b10e3b6bf)
































