Modelo de Ising

O modelo de Ising é modelo de mecânica estatística muito empregado na física do estado sólido em problemas como o lattice gas e em ligas binárias, mas é mais conhecido na descrição das propriedades magnéticas, bem como, busca simular a estrutura de uma substância ferromagnética. Obtido através de uma simplificação do modelo de Heisenberg, este é tido como um modelo dinâmico de transição de fase que incorpora interações de curto alcance numa rede d-dimensional.

Mesmo sendo conhecido como um modelo simples, uma vez que considera apenas as interações entre os spins dos vizinhos mais próximos, o modelo de Ising demonstra resultados compensatórios, podendo descrever qualitativamente vários fenômenos relacionados às transições de fase. Sua usabilidade vem do fato de que as características essenciais dos fenômenos de transição (especialmente na vizinhança próxima do ponto crítico), não serão significativamente alteradas com a inclusão das interações dos spins mais distantes.

Do mesmo modo, a substituição de uma rede estrutural por outra, desde que sua dimensionalidade seja mantida, não irá alterar significativamente as características dos fenômenos de transição de fase. Por fim, essas soluções podem ser compartilhadas, com poucas modificações, por muitos outros sistemas físicos passando por tipos muito diferentes de transições (gás-líquido ao invés de paramagnético-ferromagnético, por exemplo). Devido a essa relação íntima entre as transições de fase e o modelo de Ising, serão inicialmente abordadas as transições de fase, tão importantes para toda a física, e posteriormente o modelo de Ising propriamente dito.

Transições de fase

Em geral, o termo transição de fase pode se referir a mudanças entre os estados da matéria: sólido, líquido, gasoso e plasma, mas pode também se referir a mudanças de fase magnética, cristalina, elétrica, dentre outras.

Os fenômenos físicos aos quais o formalismo da mecânica estatística é aplicado podem, em geral, ser classificados em duas categorias. Na primeira categoria, os elementos microscópicos do sistema dado são considerados como não interagentes. Para essa situação, as funções termodinâmicas do sistema devem estar diretamente relacionadas ao conhecimento dos níveis de energia dos seus constituintes individuais. Particularmente no caso de sólidos, em que as interações desempenham um importante papel, desde que as posições dos átomos ao longo de uma grande faixa de temperaturas se mantenham próximas aos seus valores médios, é possível tratar o sólido escolhido como um “conjunto de osciladores harmônicos praticamente não interagentes”, ou seja, tratar as oscilações de um sólido com base em um gás de fônons não interagentes.. Para esta classe de fenômenos, as funções termodinâmicas são suaves e contínuas.

A segunda categoria, por sua vez, é formada por sistemas nos quais a interação interatômica não pode ser desprezada e uma mudança de coordenadas não consegue transformar as equações para um sistema equivalente de quasi-partículas não interagentes. Nesta situação, os níveis de energia do sistema total não irão estar relacionados aos níveis de energia dos elementos individuais. Em vez disso, constata-se que, em circunstâncias favoráveis, um grande número de constituintes microscópicos do sistema podem exibir uma tendência de interagir uns com os outros de uma maneira bastante forte e cooperativa. Este comportamento, assume significado macroscópico a uma temperatura comumente chamada de temperatura crítica do sistema ($T_{c}$).

Quando abordados os fenômenos pertencentes a essa segunda categoria é comum perceber-se uma mudança repentina do comportamento das propriedades termodinâmicas do sistema dado (com singularidades e descontinuidades), ou seja, transições de fase. Assim como os fenômenos críticos, as transições de fases costumam ocorrer nos mais diversos sistemas: fluidos simples e misturas, materiais magnéticos e ferroelétricos, superfluidos, supercondutores, etc. Os sistemas físico-químicos que sofrem transições de fase podem ser representados em vários graus de precisão.

As teorias clássicas das mudanças de fase em sólidos e líquidos envolvem problemas matemáticos admiráveis, que vêm sendo estudados desde 1873, quando van der Waals publicou sua tese de doutorado acerca do comportamento crítico em sistemas fluidos. Pierre Curie e Pierre Weiss, por sua vez, se dedicaram ao estudo da transição para o ferromagnetismo. Teorias dessa natureza, envolvem experiências nas vizinhanças dos pontos críticos e têm sido usadas para descrever os aspectos qualitativos de vários tipos de transições de fases.

Na região crítica (que envolve o ponto crítico), grandezas termodinâmicas como os calores específicos, a compressibilidade e a susceptibilidade magnética, apresentam um comportamento peculiar caracterizado por divergências assintóticas. Esse comportamento, por sua vez, é identificado através dos expoentes críticos.

A partir da década de 60, quando o avanço das técnicas e tecnologias permitiu que as teorias clássicas passassem por um processo mais rigoroso de análise, percebeu-se através das experiências nas vizinhanças da criticalidade que os expoentes críticos assumem valores universais, bem definidos, mas que não coincidem com as previsões das “teorias clássicas”.  Assim sendo, enquanto as teorias clássicas para sistemas distintos afirmavam que estes expoentes possuíam um caráter universal (um conjunto clássico de valores), tanto os dados experimentais quanto diversos resultados teóricos apontavam para a existência de classes de universalidade (definidas por parâmetros como a dimensionalidade dos sistemas sob consideração).

Atualmente se reconhece que os expoentes críticos são determinados por pouquíssimos fatores, entre os quais estão:

1. A dimensionalidade dos sistemas físicos;
2. A dimensionalidade do parâmetro de ordem; e
3. O alcance das interações microscópicas (nos sistemas de interesse físico as interações microscópicas serão, em geral, de curto alcance).

Tendo em vista essas questões, será discutido agora um dos mais simples e mais estudados modelos da mecânica estatística: o modelo de Ising.

Definição

Um dos fenômenos mais interessantes da física do estado sólido é o ferromagnetismo. Do mesmo modo, a magnetização espontânea dos materiais ferromagnéticos constituiu por muito tempo um problema intransponível para a física como ciência.

As primeiras teorias clássicas que tentaram explicar este problema surgiram em meados do século XIX, no entanto seu desenvolvimento completo se deu apenas com o surgimento da mecânica quântica e do conceito de spin. A partir deste momento, para explicar o ferromagnetismo, tornou-se interessante olhar para as características microscópicas do sistema e modelar o comportamento de alguns dos seus elementos.

O modelo de Ising, primeiramente proposto por Wilhelm Lenz em 1920, com o objetivo de estudar o magnetismo em materiais, foi resolvido para uma dimensão pelo seu aluno de doutorado, o estudante Ernst Ising, em 1925. Consiste em um modelo que descreve as propriedades magnéticas de um sólido através das suas propriedades microscópicas, mais especificamente do comportamento de spins localizados e suas interações. O modelo de Ising é essencialmente um caso particular do modelo de Heisenberg que constrói um hamiltoniano baseado nas interações de troca entre os spins. O hamiltoniano de Heisenberg é escrito como

${\cal {H}}=-\sum _{ij}J{\bf {{S}_{i}\cdot {\bf {{S}_{j}}}}}$

Que consiste em uma soma dupla sobre a interação de troca J de cada spin i com seus primeiros vizinhos j.

No modelo de Heisenberg os spins são tratados como vetores, ou seja, possuem componentes nas três dimensões espaciais, neste caso dizemos que a dimensionalidade d do spin é 3. Também é importante destacar que esta soma depende de uma rede na qual os spins estão localizados, podendo esta rede também possuir uma dimensionalidade D. O parâmetro J é uma medida da interação entre os spins que em geral depende da ordem do vizinho (primeiros vizinhos, segundos vizinhos). Se considerarmos apenas primeiros vizinhos, J pode sair do somatório de forma a obtermos

${\cal {H}}=-J\sum _{ij}{\bf {{S}_{i}\cdot {\bf {{S}_{j}}}}}$

Abrindo o produto escalar,

${\cal {H}}=-J\sum _{ij}S_{i}^{x}S_{j}^{x}+S_{i}^{y}S_{j}^{y}+S_{i}^{z}S_{j}^{z}$

O modelo de Ising considera a dimensionalidade do spin d = 1, ou seja, apenas uma das componentes aparece, por exemplo a direção z:

$H=-J\sum _{ij}S_{i}^{z}S_{j}^{z}$

Note que neste caso surge uma anisotropia no modelo de Ising, ou seja, há uma direção cujas as propriedades serão diferentes das demais, neste caso a direção z. É importante destacar que o modelo de Heisenberg é essencialmente isotrópico.

Embora Ernst tenha obtido com o modelo de Ising resultados interessantes acerca das propriedades termodinâmicas, ele pode perceber que o caso em uma dimensão não possuía transição de fase ou magnetização espontânea.

A demonstração da transição de fase ocorreu, por sua vez, em 1944, quando Lars Onsager resolveu por aproximação o modelo bidimensional de Ising na ausência de um campo magnético. O cálculo por aproximação, feito para funções termodinâmicas com descontinuidades é bastante complicado visto que, a convergência da aproximação por funções analíticas em tais casos é lenta. Sem nenhuma aproximação, a solução analítica tanto para duas como para três dimensões seria impossível.

O modelo de Ising bidimensional cede a um tratamento exato na mecânica estatística. Esse é o único exemplo não trivial de uma transição de fase que pode ser trabalhada com rigor matemático. O nome modelo de Ising foi popularizado após o artigo de R. Peierls, publicado em 1936 com o título “On Ising’s Model of Ferromagnetism”.

A proposta de explicação que o modelo de Ising usa para a magnetização espontânea é baseada no conceito de interação de troca. Para modelarmos essa situação teremos que considerar então os termos referentes à energia no estado fundamental, àqueles relativos à interação coulombiana (interação entre partículas eletricamente carregadas) além, é claro, do termo associado à interação de troca.

A hamiltoniana de Heisenberg, assim como segue, é a responsável maior por definir a interação de troca entre os elétrons dando origem ao já citado modelo isotrópico de Heisenberg.

$H=-J\textstyle \sum _{i,j}\displaystyle (\sigma _{i}^{x}\sigma _{j}^{x}+\sigma _{i}^{y}\sigma _{j}^{y}+\sigma _{i}^{z}\sigma _{j}^{z})$

Na equação acima J é a interação de troca entre os spins $\sigma _{i}$ e $\sigma _{j}$, bem como x, y e z são as direções das suas componentes. A hamiltoniana de Ising, por sua vez, surge de uma particularização da hamiltoniana de Heisenberg, ou seja, para descrever um sistema cujos spins apontam para uma única direção (direção z, por exemplo). Veja a seguir a hamiltoniana de Ising.

$H=-J\textstyle \sum _{i,j}\displaystyle \sigma _{i}^{z}\sigma _{j}^{z}$

Por ter uma posição favorecida, o modelo de Ising é dito anisotrópico, ou seja, suas propriedades físicas devem variar com a direção.

Aproximação de ordem zero

A fim de descrever a teoria microscópica das transições de fase foram desenvolvidos alguns modelos matemáticos. O modelo de Ising, como citado anteriormente, busca descrever tais transições, para tanto considera as interações de curto alcance entre os spins dos átomos imediatamente mais próximos (chamados primeiros vizinhos) de um átomo específico em uma rede d-dimensional.

Algumas técnicas foram desenvolvidas com o intuito de encontrar a solução para o modelo de Ising, essas técnicas formam o pequeno conjunto de ferramentas disponíveis para para descrever sistemas complexos. Duas técnicas podem ser destacadas, são elas a aproximação de ordem zero e a primeira aproximação.

A partir das tentativas de desenvolver estudos estatísticos de transição de fase do tipo ordem-desordem, Gorsky em 1928 supôs que o trabalho gasto para mudar um átomo de uma posição ordenada para uma desordenada era diretamente proporcional ao grau de ordem do sistema. A ideia foi desenvolvida por Bragg e Williams em 1934 e 1935 respectivamente, que pela primeira vez introduziram a ideia de parâmetro de longo alcance.

Nessa aproximação, a ideia central consiste em isolar um spin da rede e considerar a existência de um valor fixo para a magnetização dos demais spins, de modo que é possível supor a existência de um campo magnético interno médio, que interage com o spin isolado, permitindo assim desprezar as interações entre os pares de spins vizinhos e as flutuações causadas na função de correlação, que se estendem fora da célula fixada da rede. Desta forma a aproximação de ordem zero considera somente as flutuações que ocorrem na célula fixada, ou seja, envolve somente as flutuações que ocorrem com um único spin fixo.

Ao fixar um único spin da rede e considerar a interação deste com os demais, a partir de um campo médio de magnetização, o problema de mecânica estatística de muitos corpos é reduzido para um problema de um único corpo. Essa aproximação, por sua vez, carrega certo grau de inexatidão, especialmente quando são envolvidos os sistemas próximos do ponto crítico, em que as flutuações se estendem a grandes distâncias. Mas, apesar dessa aproximação não fornecer resultados exatos, ela pode ser muito útil, como por exemplo, na descrição de propriedades termodinâmicas de sistemas em regiões de altas temperaturas, onde não é esperado a existência de correlação entre o spin e seus primeiros vizinhos. Existem ainda algumas versões mais sofisticadas do modelo da aproximação de ordem zero, que consistem em fixar mais de um spin da rede, a exemplo de um par de spins vizinhos, reduzindo o problema de vários corpos a um problema de dois corpos e fornecendo resultados mais precisos.

Em um modelo de spin ½ , para uma rede com N spins, N representa o número total de spins dado pela soma de todos os spins Up da rede ($N_{+}$) com todos spins Down ($N_{-}$). Defini-se o parâmetro de ordem de longo alcance ($L$) nesse sistema na forma,

$L=\left({\frac {1}{N}}\right)\sum _{i}\sigma _{i}$

note que $L$ é um parâmetro médio e representa a média da correlação de spin (${\overline {\sigma _{i}}}$). A equação acima pode ser escrita como:

$L=\left({\frac {N_{+}-N_{-}}{N}}\right).$

A magnetização por sua vez, é expressa como o produto da diferença entre a quantidade de spins Up e Down e pelo momento magnético ($\mu$), matematicamente tem-se que:

$M=(N_{+}-N_{-})\mu ,$

que ainda, pode ser reescrita na forma:

$M=N.L.\mu$

evidenciando a dependência que a magnetização possui em relação ao parâmetro de ordem de longo alcance.

O hamiltoniano deste sistema, que possui a forma dada por:

$H\{\sigma _{i}\}=-J\textstyle \sum _{nm}\displaystyle \sigma _{i}\sigma _{j}-\mu B\textstyle \sum _{i}\displaystyle \sigma _{i}$

pode ser reescrito, ficando da seguinte maneira:

$H\{\sigma _{i}\}=-{\frac {jq{\overline {L}}}{2}}\textstyle \sum _{i}\displaystyle \sigma _{i}-\mu B\textstyle \sum _{i}\displaystyle \sigma _{i}.$

Nesta equação, q representa o número de coordenação, isto é, a quantidade de vizinhos imediatamente  mais próximos do spin fixado (em uma rede unidimensional q = 2 e em uma rede bidimensional q = 4) e B representa o campo magnético externo.

O hamiltoniano pode ser resolvido, de forma a denotar o valor da energia do sistema,  que vale:

$E=-{\frac {NqJ{\overline {L}}}{2}}L-\mu BNL.$

De modo que a energia média para esse sistema é dada de forma semelhante:

$E_{(}med)=U=-{\frac {NqJ{\overline {L}}^{2}}{2}}-\mu BN{\overline {L}}.$

A diferença de energia ($\Delta \varepsilon$) para trocar um spin Up por um Down, por sua vez, é descrita como:

$\Delta \varepsilon \approx 2\mu {\Biggl (}{\frac {qJ\sigma }{\mu }}+B{\Biggr )}.$

Fazendo $B\prime ={\frac {qJ\sigma }{\mu }}$, a equação passa a ter a seguinte forma:

$\Delta \varepsilon \approx 2\mu {\Biggl (}B\prime +B{\Biggr )}$

onde $B\prime$ representa o campo magnético interno do sistema.

As condições para mudança de fase são determinadas a partir da relação a seguir,

${\frac {\overline {N_{-}}}{\overline {N_{+}}}}=\exp({\frac {-\Delta \varepsilon }{kT}}).$

Quando realizados os tratamentos matemáticos adequados é obtida a seguinte relação,

${\overline {L_{o}}}=\tanh {\Biggl (}{\frac {qJ{\overline {L}}+\mu B}{kT}}{\Biggr )}$

que, na ausência do campo magnético externo se reduz a

${\overline {L_{o}}}=\tanh {\Biggl (}{\frac {qJ{\overline {L_{o}}}}{kT}}{\Biggr )}.$

A equação acima pode ser resolvida graficamente, de modo que sua solução indica uma temperatura crítica ($T_{c}$), a partir da qual é possível definir o início da transição de fase ferromagnética. Essa temperatura recebe o nome de temperatura de Curie, que pode ser expressa matematicamente por,

$T_{c}={\frac {qJ}{k}}.$

Quando o sistema sai de um estado com temperaturas maiores que $T_{c}$ e passa para um estado com temperatura menores, ocorre uma transição de fase. Durante este fenômeno os spins da rede passam por um processo chamado de acoplamento, se alinhando na mesma direção e sentido, de modo que o sistema passa a apresentar magnetização espontânea.

O calor específico para este sistema, por sua vez, pode ser expresso da seguinte maneira,

$C_{o}(T)\approx 4Nk{\Biggl (}{\frac {T_{c}}{T}}{\Biggr )}^{2}\exp {\Biggl (}{\frac {-2T_{c}}{T}}{\Biggr )}.$

Por intermédio dessa equação é possível notar que quando $T\rightarrow T_{c}$ o calor específico do sistema desaparece, isto ocorre pois para temperaturas elevadas não há magnetização espontânea.

Aproximação de primeira ordem

Aglomerado com spin central e seus spins vizinhos.

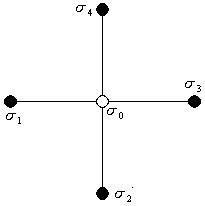
As aproximações estabelecidas para o modelo de Ising de ordem zero são bastante genéricas, podendo ser aprimoradas quando considera-se a correlação de um dado spin entre os vizinhos próximos. Essas ponderações definem a chamada aproximação de Bethe, desenvolvida por Bethe e Rushbrooke, também conhecida como aproximação de primeira ordem do modelo de Ising, que considera que um dado spin, tem q vizinhos próximos, e cada ponto da rede é também associado aos seus respectivos spins ($\sigma _{0},...,\sigma _{j},...,$), conforme ao lado, levando em conta as trocas de energia ($J_{0i},...,J_{ij},...,$) entre seus pares, através de suas interações.

Para esse modelo considera-se $J_{iJ}$ desprezível, exceto para seus pares mais próximos, já que essa interação fica menos evidente conforme aumentam-se as distâncias entre o spin central ($\sigma _{0}$) e os demais ($\sigma _{j}$). Essa observação permite que essa troca de energia, no caso de interações isotrópicas, seja definida simplesmente pelo símbolo J, tendo em vista que para J>0 tem-se o caso do ferromagnetismo (caso de interesse) e para J<0 o antiferromagnetismo.

O hamiltoniano deste sistema, onde o spin central interage a curto alcance com seus primeiros vizinhos é dado por,

$H_{q+1}=-\mu B\sigma _{0}-\mu (B+B')\sum _{j=1}^{q}\sigma _{j}-J\sum _{j=1}^{q}\sigma _{0}\sigma _{j}$

onde, $B$ representa o campo magnético externo atuando sobre a rede de spins e $B'$ o campo magnético interno, que obedece ao princípio da auto consistência. Esse princípio está relacionado a afirmação de que ambas expressões devem ser assintoticamente equivalentes impondo que o valor médio de spin central da rede  ${\overline {\sigma _{0}}}$, seja igual ao valor médio de spin ${\overline {\sigma _{J}}}$, de qualquer um dos $q$ vizinhos. Assim a função partição ($Z$) do sistema fica:

$Z=\sum _{\sigma _{0},\sigma _{j}=\pm 1}exp{\bigg [}{\frac {1}{kT}}{\bigg \{}\mu B\sigma _{0}+\mu (B+B')\sum _{j=1}^{q}\sigma _{j}+J\sum _{j=1}^{q}\sigma _{0}\sigma _{j}{\bigg \}}{\bigg ]}$

de modo que considerando as seguintes variáveis

$\alpha ={\frac {\mu B}{kT}}$, $\alpha '={\frac {\mu B'}{kT}}$ e $\gamma ={\frac {J}{kT}}$

obtém-se

$Z=\sum _{\sigma _{0},\sigma _{j}=\pm 1}exp{\bigg [}\alpha \sigma _{0}+(\alpha +\alpha ')\sum _{j=1}^{q}\sigma _{j}+\gamma \sum _{j=1}^{q}\sigma _{0}\sigma _{j}{\bigg ]}$

A função partição canônica, pode ser escrita como o somatório de dois termos, pertencentes a $\sigma _{0}=1$ (spin Up) e $\sigma _{0}=-1$ (spin Down),

$Z=Z_{+}+Z_{-}$

o que resulta em

$Z_{\pm }=\sum _{\sigma _{j}=\pm 1}exp{\bigg [}\pm \alpha +(\alpha +\alpha '\pm \gamma )\sum _{j=1}^{q}\sigma _{j}{\bigg ]}$,

$Z_{\pm }=e^{\pm \alpha }[2cosh(\alpha +\alpha '\pm \gamma )]^{q}$.

O valor médio do spin central é então dado por

${\overline {\sigma _{0}}}={\frac {Z_{+}-Z_{-}}{Z}}$

e, conforme segue, os spins dos $q$ vizinhos ficam

${\overline {\sigma _{0}}}={\frac {1}{Z}}{\big \{}Z_{+}tanh(\alpha +\alpha '+\gamma )+Z_{-}tanh(\alpha +\alpha '+\gamma ){\big \}}$

que, considerando a condição de autoconsistência do campo B’ será

${\overline {\sigma _{0}}}={\overline {\sigma _{j}}}={\overline {\sigma }}$

Substituindo $Z_{+}$ e $Z_{-}$ nas expressões obtidas anteriormente para a função partição, na expressão acima para $\sigma$,

$Z_{+}=e^{+\alpha }[2cosh(\alpha +\alpha '+\gamma )]^{q}$

$Z_{-}=e^{-\alpha }[2cosh(\alpha +\alpha '-\gamma )]^{q}$

Temos a seguinte relação

$e^{2\alpha '}={\bigg \{}{\frac {cosh(\alpha +\alpha '+\gamma )}{cosh(\alpha +\alpha '-\gamma )}}{\bigg \}}^{q-1}$

Esta expressão leva a equação de estado desta aproximação e representa o comportamento magnético da rede de spins. Pode-se obter algumas informações quando levado em conta as variáveis $\alpha$, $\alpha '$ e $\gamma$, que estão diretamente relacionadas à temperatura $T$, campo externo $B$, campo interno $B'$ e a energia de interação J.

Considerando o campo magnético externo $B=0$, tem-se que $\alpha =0$ na expressão acima, que resultará na condição de magnetização espontânea. A equação de estado se torna então:

$\alpha '={\frac {q-1}{2}}ln{\bigg \{}{\frac {cosh(\alpha '+\gamma )}{cosh(\ \alpha '-\gamma )}}{\bigg \}}$.

Se o sistema não apresenta interações, se tem$\gamma =0$, e $\alpha '=0$. Por sua vez, quando as interações são levadas em conta, com $\gamma \neq 0$, a expressão para $\alpha '$ deverá ser escrita em termos de uma expansão em série de Taylor, o que resulta na relação:

$\alpha '=(q-1)tanh\gamma {\Big \{}\alpha '-sech^{2}\gamma {\frac {\alpha '^{3}}{3}}+...{\Big \}}$

que levará após um tratamento matemático elaborado, a relação:

$T<T_{c}={\frac {\frac {2J}{k}}{ln({\frac {q}{q-2}})}}$

que determina a temperatura de Curie da rede.

Pode-se perceber que o parâmetro q está relacionado com a configuração dimensional da rede, onde em uma dimensão (isto é, para $q=2$), não ocorre transição de fase, $T_{c}=0$. Já para $q=4$ (o que corresponde a uma rede quadrada), temos ${\frac {kT_{c}}{j}}={\frac {2}{ln2}}=2,885...$ , sendo inferior ao valor previsto por Bragg-Williams ${\frac {kT_{c}}{J}}=4$ e ainda acima dos previsto por Onsager ${\frac {kT_{c}}{J}}={\frac {2}{ln(1+{\sqrt {2}})}}=2,269...$ .

Tomando a afirmação para a aproximação de Bragg-Williams,  que afirma que “não há nenhuma ordem de curto alcance além daquela estabelecida na ordem de longo alcance”, é possível expressar o parâmetro de ordem de longo alcance ${\overline {L}}$ igual ao parâmetro ordem de curto alcance ${\overline {\sigma }}$ na rede, logo:

${\overline {L}}={\frac {(Z_{+}+Z_{-})-1}{(Z_{+}+Z_{-})+1}}={\frac {sinh(2\alpha +2\alpha ')}{cosh(2\alpha +2\alpha ')+exp(-2\gamma )}}$.

E no limite $B\rightarrow 0$ considerando temperaturas menores mais próximas da temperatura de Curie, chega-se a:

${\overline {L_{0}}}\simeq {\bigg [}3{\frac {q}{q-1}}{\bigg \{}{\frac {q}{2}}ln{\bigg (}{\frac {q}{q-2}}{\bigg )}{\bigg \}}{\bigg (}1-{\frac {T}{T_{c}}}{\bigg )}{\bigg ]}^{1/2}$

Uma correspondência com a aproximação de ordem zero pode ser obtida se for considerado $q\gg 1$ na equação acima. Também nota-se que a curva de magnetização espontânea, apresenta comportamento similar ao de ordem zero , ainda que dependendo explicitamente do valor $q$.

Se consideradas as correlações existentes entre os spins vizinhos na rede, pode-se avaliar os números $N_{++}$, $N_{--}$ e $N_{+-}$ (onde cada um dos termos representa o número total de pares de spins conforme indicado nos índices), em função dos parâmetros $\alpha$, $\alpha '$, e $\gamma$. Modificando os somatórios na expressão da função partição canônica do sistema, é possível escrever para $\sigma _{0}=\sigma _{1}=+1$ , $\sigma _{0}=-\sigma _{1}=-1$  e $\sigma _{0}=-\sigma _{1}=\pm 1$ :

$Z=Z_{++}+Z_{--}+Z_{+-}$

Como a função partição está diretamente ligada aos números $N_{++}$, $N_{--}$ e $N_{+-}$, pode-se reescrever, usando a equação de estado da aproximação, considerando que são diretamente proporcionais as funções partição $Z_{++}$, $Z_{--}$ e $Z_{+-}$ com a devida normalização,

$({\overline {N_{++}}},{\overline {N_{--}}},{\overline {N_{+-}}})={\frac {1}{2}}qN{\frac {(e^{2\alpha +2\alpha '+\gamma },e^{-2\alpha -2\alpha '+\gamma },2e^{-\gamma })}{2{\big \{}e^{\gamma }cosh(2\alpha +2\alpha '){\big \}}}}$

onde

${\frac {{\overline {N_{++}}}{\overline {N_{--}}}}{\overline {N_{}+-}}}={\frac {1}{4}}e^{4\gamma }={\frac {1}{4}}^{4J/kT}$

A presença do fator $exp(4J/kT)$ para o caso do ferromagnetismo, favorece a formação de pares de spin paralelos $\uparrow \uparrow$ e $\downarrow \downarrow$, ao invés de pares de spins antiparalelos $\uparrow \downarrow$ e $\downarrow \uparrow$. Em termos de correlação isso significa dizer: positivo para spins vizinhos $\uparrow \uparrow$ ou $\downarrow \downarrow$ e negativo para spins vizinhos $\uparrow$ e $\downarrow$.

Comparações entre as aproximações

A aproximação de ordem zero (chamada também de aproximação de campo médio ou de Bragg-Williams) supõe que a energia de um átomo em um determinado sistema é definida pelo grau de ordem que domina o mesmo e não pelas configurações (flutuações) com os átomos vizinhos. Já a aproximação de primeira ordem (ou aproximação de Bethe), considera a interação de um spin central e seus vizinhos mais próximos, de modo que o hamiltoniano do grupo é dado pela interação do spin central com seus vizinhos somado à interação desses vizinhos com o resto da rede por um campo molecular médio, como considerado na aproximação zero.

A diferença na forma de construção das aproximações de ordem zero e primeira ordem, conduz a um resultado para o calor específico e energia interna do sistema, que torna o modelo de primeira ordem mais próximo dos sistemas físicos reais. Pode-se obter facilmente a equação para energia interna de ordem zero a partir da energia média do sistema, quando $B\rightarrow 0$,

$C_{o}={\frac {Nk{\overline {L_{o}}}^{2}}{{\frac {{\Biggl (}{\frac {T}{T_{c}}}{\Biggr )}^{2}}{1-{\overline {L_{o}}}^{2}}}-{\frac {T}{T_{c}}}}}$

Quando a temperatura se aproxima da temperatura crítica a partir de temperaturas menores que ela, o calor específico acima apresenta uma descontinuidade no ponto de transição, de acordo com a equação abaixo.

$C_{o}={\frac {3}{2}}Nk$

e quando $T\rightarrow 0$, o calor específico desaparece pois:

$C_{o}(T)\approx 4Nk{\Biggl (}{\frac {T_{c}}{T}}{\Biggr )}^{2}\exp {\Biggl (}{\frac {-2T_{c}}{T}}{\Biggr )}$

Pode-se obter a energia interna e o calor específico da aproximação de primeira ordem, através da energia de configuração média na ausência de um campo externo, dada por:

$U_{o}(T)=-J{\Biggl (}{\frac {1}{2}}qN-2q{\overline {N}}_{+}+4{\overline {N}}++{\Biggr )}$

A partir da  medida do parâmetro de longo alcance no sistema (${\overline {L}}$), obtemos os ${\overline {N}}_{+}$ e ${\overline {N}}++$, que aplicadas na expressão de energia e desenvolvidas conduzem ao resultado:

$U_{o}=-{\frac {1}{2}}qJN{\frac {\cosh(2\alpha ^{\prime })-\exp(-2\gamma )}{\cosh(2\alpha ^{\prime })+\exp(-2\gamma )}}.$

Para temperatura $T>T_{c}$ e $\alpha \prime =0$, a energia interna e o calor específico serão dados como segue:

$U_{o}=-{\frac {1}{2}}qJN\tanh(\gamma ),$

${\frac {C_{o}}{Nk}}={\frac {1}{2}}q\gamma ^{2}\operatorname {sech} ^{2}(\gamma ).$

Na equação do calor específico para primeira ordem e ordem zero, quando  $T\rightarrow \infty$, o calor específico tende a zero. Entretanto para $T>T_{c}$, o calor específico obtido pela aproximação de Bethe conduz a um valor não nulo, devido a interação de curto alcance do spin central com seus spins vizinhos. Em contraste, a aproximação de Bragg-Williams, apresenta uma descontinuidade no calor específico em $T=T_{c}$, se anulando em valores acima da temperatura crítica. Para todo q a primeira aproximação produz uma temperatura de transição mais próxima do valor correto da temperatura crítica, do que a aproximação de ordem zero.

Assim como o calor específico, é possível analisar também a energia interna em ambas aproximações. A energia interna é contínua na aproximação de Bethe, acima da temperatura crítica, como era de se esperar, dado que o calor específico se mantém nessa aproximação, devido a interação de curto alcance entre os spins. Já aproximação de Bragg-Williams, a energia interna é nula, para toda temperatura acima da temperatura crítica, resultado esse consistente com o gráfico de calor específico.

Simulação computacional

O modelo de Ising foi implementado usando o algoritmo de Metropolis através de CUDA GPU e está disponível num repositório de GitHub

Simulação de Monte-Carlo de transições de fase em magnéticos, a uma temperatura T = 3. Os spins para cima/para baixo (ímãs) são pixels preto/branco,

Como já discutido anteriormente, o ferromagnetismo é um dos fenômenos da física dos sólidos mais relevantes. Quando uma temperatura é menor que a temperatura crítica ou temperatura de Curie (Tc), em alguns metais, uma pequena parte (finita) dos spins dos átomos, de mesma direção, é naturalmente polarizada gerando assim um campo magnético macroscópico.

Simulação de Monte-Carlo de transições de fase em magnéticos, para temperatura inferiores a temperatura critica.

Por sua vez, quando a temperatura é maior que a temperatura de Curie não é gerado nenhum campo magnético e nesse caso os spins são orientados de forma aleatória. À medida que se aproxima da temperatura de Curie por ambos os lados, o calor específico do metal tende ao infinito. Essa breve abordagem permitirá a compreensão do simulador fps Monte-Carlo de transições de fase no magnetismo (disponível: https://ibiblio.org/e-notes/Perc/ising1k.htm).

A transição de fase magnética ocorre em Tc = 2,269 (valor considerado pelo simulador). Quando a temperatura for T = 1 (T < Tc), as rotações aleatórias do spin são fixadas em grupos pretos e brancos correlacionados. Ao definir T = 3 é possível perceber que os spins voltam ao seu comportamento aleatório. (As imagens ao lado ilustram os resultados aproximado obtido no simulado). Após ocorrer a transição de fase as flutuações permanecem, porém é possível notar a formação de regiões com mesma orientação de spin, ou seja, regiões com a mesma cor (preta ou branca). Quanto menor for a temperatura menores serão as flutuações e as regiões pretas dentro das brancas (e vice-versa) vão desaparecendo. Ao elevar-se a temperatura o acoplamento entre os spins vai diminuir e ao se atingir T maior que Tc essa ligação será destruída, voltando a ter um comportamento aleatório.

Aplicações interdisciplinares

O modelo de Ising foi inicialmente desenvolvido para entender melhor o ferromagnetismo, mas no decorrer do tempo diversas aplicações interdisciplinares foram sendo desenvolvidas em biologia, neurociência, dinâmicas sociais e economia.

Bibliografia

• Barry M. McCoy and Tai Tsun Wu (1973), The Two-Dimensional Ising Model. Harvard University Press, Cambridge Massachusetts, ISBN 0-674-91440-6
• Ross Kindermann and J. Laurie Snell (1980), Markov Random Fields and Their Applications. American Mathematical Society. ISBN 0-8218-3381-2.
• Stephen G. Brush (1967), History of the Lenz-Ising Model. Reviews of Modern Physics (American Physical Society) vol. 39, pp 883–893. (DOI: 10.1103/RevModPhys.39.883)
• I. A. Stepanov. Exact Solutions of the One-Dimensional, Two-Dimensional, and Three-Dimensional Ising Models. – Nano Science and Nano Technology: An Indian Journal. 2012. Vol. 6. No 3. 118 - 122. The paper is on the Journal’s website with a free access.

Ligações externas

• Barry A. Cipra, "The Ising model is NP-complete", SIAM News, Vol. 33, No. 6; online edition (.pdf)
  • Reports why the Ising model can't be solved exactly in general, since non-planar Ising models are NP-complete.
• Science World article on the Ising Model
• An Ising Applet by Syracuse University
• A nice dynamical 2D Ising Applet
• A larger/more complicated 2D Ising Applet
• Ising Model simulation by Enrique Zeleny, the Wolfram Demonstrations Project
• Phase transitions on lattices
• Three-dimensional proof for Ising Model impossible, Sandia researcher claims
• 3D Ising model simulation on GPU