Processo de Wiener

Uma representação simples de um processo de Wiener unidimensional

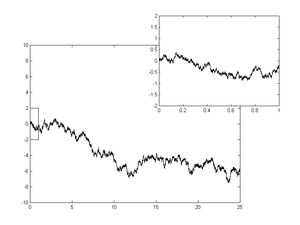
Em matemática, o processo de Wiener é um processo estocástico de tempo contínuo, que recebe este nome em homenagem a Norbert Wiener. É frequentemente chamado de processo de movimento browniano padrão ou movimento browniano devido a sua conexão histórica com o processo físico conhecido como movimento browniano primeiramente observado por Robert Brown. Foi também estudado por Albert Einstein. É um dos mais conhecidos processos de Lévy (processos estocásticos càdlàg com incrementos independentes estacionários) e ocorre frequentemente em matemática pura e aplicada, economia, matemática financeira e física.

Uma representação simples de um processo de Wiener tridimensional

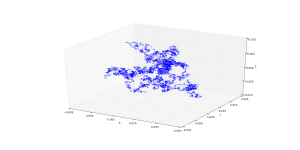
O processo de Wiener desempenha um papel importante tanto na matemática pura, quanto na aplicada. Em matemática pura, o processo de Wiener fez surgir o estudo de martingales de tempo contínuo. É um processo-chave em cujos termos processos estocásticos mais complicados podem ser descritos, em especial, por ser um dos únicos processos que é, ao mesmo tempo, martingale e markoviano. Como tal, desempenha um papel vital no cálculo estocástico, nos processos de difusão e, até mesmo, na teoria do potencial. É o processo condutor da evolução de Schramm-Loewner. Em matemática aplicada, o processo de Wiener é usado para representar a integral de um processo gaussiano de ruído branco, que é útil no que se refere a modelos de ruído na engenharia eletrônica (veja ruído browniano), erros de instrumento em teoria da filtragem e forças desconhecidas em teoria de controle.

O processo de Wiener tem aplicações por todas as ciências matemáticas. Em física, é usado para estudar o movimento browniano, a difusão de partículas mínimas suspensas em fluido, e outros tipos de difusão via equações de Langevin e Fokker-Planck. Também constitui a base da formação de integrais de caminho da mecânica quântica (pela fórmula de Feynman-Kac, uma solução à equação de Schrödinger que pode ser representada nos termos do processo de Wiener) e do estudo da inflação eterna na cosmologia física. Também é proeminente na teoria matemática das finanças, em particular no modelo Black-Scholes de precificação de opções.

Caracterizações do processo de Wiener

O processo de Wiener $W_{t}$ é caracterizado pelas seguintes propriedades:

1. $W_{0}=0$ q.c.
2. $W$ tem incrementos independentes: para todo $t>0$, os incrementos futuros $W_{t+u}-W_{t}$, $u\geq 0$, são independentes dos valores passados $W_{s}$, $s\leq t$.
3. $W$ tem incrementos gaussianos: $W_{t+u}-W_{t}$ é normalmente distribuído com média $0$ e variância $u$, $W_{t+u}-W_{t}\sim {\mathcal {N}}(0,u)$
4. $W$ tem caminhos contínuos: com probabilidade $1$, $W_{t}$ é contínuo em $t$.

Por incrementos independentes, diz-se que, se $0\leq s_{1}<t_{1}\leq s_{2}<t_{2}$_, então $W_{t1}-W_{s1}$ e $W_{t2}-W_{s2}$ são variáveis aleatórias independentes e a mesma condição se mantém para $n$ incrementos.

Uma caracterização alternativa do processo de Wiener é a então chamada caracterização de Lévy, que diz que o processo de Wiener é um martingale quase certamente contínuo com $W_{0}=0$ e variação quadrática $[W_{t},W_{t}]=t$ (o que significa que $W_{t}^{2}-t$ é também um martingale).

Uma terceira caracterização diz que o processo de Wiener tem um representação espectral como uma série de senos cujos coeficientes são variáveis aleatórias independentes $N(0,1)$. Esta representação pode ser obtida usando o teorema de Karhunen-Loève.

Outra caracterização de um processo de Wiener é a integral definida (de $0$ ao tempo $t$) de um processo gaussiano ("branco") delta-correlacionado com variância $1$ e média $0$.

O processo de Wiener pode ser construído como o limite escalar de um passeio aleatório ou outros processos estocásticos de tempo discreto com incrementos independentes estacionários. Isto é conhecido como teorema de Donsker. Assim como o passeio aleatório, o processo de Wiener é recorrente em uma ou duas dimensões (o que significa que ele retorna quase certamente a qualquer vizinhança fixada da origem infinitas vezes), mas não é recorrente em três ou mais dimensões. Diferentemente do passeio aleatório, tem como característica a invariância de escala, o que significa que

$\alpha ^{-1}W_{\alpha ^{2}t}$

é um processo de Wiener para qualquer constante $\alpha$ não nula. A medida de Wiener é a lei probabilística no espaço das funções contínuas $g$, com $g(0)=0$, induzido pelo processo de Wiener. Uma integral baseada na medida de Wiener pode ser chamada de integral de Wiener.

Processo de Wiener como um limite do passeio aleatório

Considere $\xi _{1},\xi _{2},\ldots$ variáveis aleatórias independentes e identicamente distribuídas com média $0$ e variância $1$. Para cada $n$, defina um processo estocástico de tempo contínuo

$W_{n}(t)={\frac {1}{\sqrt {n}}}\sum \limits _{1\leq k\leq \lfloor nt\rfloor }\xi _{k}$

Esta é uma função passo aleatório. Incrementos de $W_{n}$ são independentes porque $\xi _{k}$ são independentes. Para $n$ grande, $W_{n}(t)-W_{n}(s)$é próximo de $N(0,t-s)$ pelo teorema central do limite. Conforme $n\to \infty$, $W_{n}$ se aproximará de um processo de Wiener. A prova desta afirmação é oferecida pelo teorema de Donsker. Esta formulação explicou por que o movimento browniano é ubíquo.

Propriedades de um processo de Wiener unidimensional

Propriedades básicas

A função densidade de probabilidade incondicional, que segue distribuição normal com média igual a $0$ e variância igual a $t$, em um tempo fixado $t$:

$f_{W_{t}}(x)={\frac {1}{\sqrt {2\pi t}}}e^{-x^{2}/(2t)}.$

O valor esperado é zero:

$E[W_{t}]=0.$

A variância, usando a fórmula algébrica para a variância, é t:

$\operatorname {Var} (W_{t})=E\left[W_{t}^{2}\right]-E^{2}[W_{t}]=E\left[W_{t}^{2}\right]-0=E\left[W_{t}^{2}\right]=t.$

Covariância e correlação

A covariância e a correlação:

$\operatorname {cov} (W_{s},W_{t})=\min(s,t),$

$\operatorname {corr} (W_{s},W_{t})={\frac {\operatorname {cov} (W_{s},W_{t})}{\sigma _{W_{s}}\sigma _{W_{t}}}}={\frac {\min(s,t)}{\sqrt {st}}}={\sqrt {\frac {\min(s,t)}{\max(s,t)}}}.$

Os resultados para o valor esperado e a variância seguem imediatamente da definição de que os incrementos têm uma distribuição normal, centrada em zero. Assim

$W_{t}=W_{t}-W_{0}\sim N(0,t).$

Os resultados para a covariância e a correlação seguem da definição de que incrementos não sobrepostos são independentes, da qual apenas a propriedade de que eles não são correlacionados é usada. Suponha que $t_{1}<t_{2}$.

$\operatorname {cov} (W_{t_{1}},W_{t_{2}})=\operatorname {E} \left[(W_{t_{1}}-\operatorname {E} [W_{t_{1}}])\cdot (W_{t_{2}}-\operatorname {E} [W_{t_{2}}])\right]=\operatorname {E} \left[W_{t_{1}}\cdot W_{t_{2}}\right].$

Substituindo

$W_{t_{2}}=(W_{t_{2}}-W_{t_{1}})+W_{t_{1}}$

Chegamos em:

${\begin{aligned}\operatorname {E} [W_{t_{1}}\cdot W_{t_{2}}]&=\operatorname {E} \left[W_{t_{1}}\cdot ((W_{t_{2}}-W_{t_{1}})+W_{t_{1}})\right]\\&=\operatorname {E} \left[W_{t_{1}}\cdot (W_{t_{2}}-W_{t_{1}})\right]+\operatorname {E} \left[W_{t_{1}}^{2}\right].\end{aligned}}$

Já que $W(t_{1})=W(t_{1})-W(t_{0})$ e $W(t_{2})-W(t_{1})$ são independentes,

$\operatorname {E} \left[W_{t_{1}}\cdot (W_{t_{2}}-W_{t_{1}})\right]=\operatorname {E} [W_{t_{1}}]\cdot \operatorname {E} [W_{t_{2}}-W_{t_{1}}]=0.$

Assim

$\operatorname {cov} (W_{t_{1}},W_{t_{2}})=\operatorname {E} \left[W_{t_{1}}^{2}\right]=t_{1}.$

Representação de Wiener

Wiener (1923) também deu uma representação de um caminho browniano em termos de uma série aleatória de Fourier. Se $\xi _{n}$ são variáveis gaussianas independentes com média $0$ e variância $1$, então

$W_{t}=\xi _{0}t+{\sqrt {2}}\sum _{n=1}^{\infty }\xi _{n}{\frac {\sin \pi nt}{\pi n}}$

e

$W_{t}={\sqrt {2}}\sum _{n=1}^{\infty }\xi _{n}{\frac {\sin \left(\left(n-{\frac {1}{2}}\right)\pi t\right)}{\left(n-{\frac {1}{2}}\right)\pi }}$

representa um movimento browniano em $[0,1]$. O processo escalado

${\sqrt {c}}\,W\left({\frac {t}{c}}\right)$

é um movimento browniano em $[0,c]$ (vide teorema de Karhunen-Loève).

Máximo corrente

A distribuição conjunta do máximo corrente

$M_{t}=\max _{0\leq s\leq t}W_{s}$

e $W_{t}$ é

$f_{M_{t},W_{t}}(m,w)={\frac {2(2m-w)}{t{\sqrt {2\pi t}}}}e^{-{\frac {(2m-w)^{2}}{2t}}},\qquad m\geq 0,w\leq m.$

Para obter a distribuição incondicional de $f_{M_{t}}$, integra-se ao longo de $-\infty <w\leq m$:

${\begin{aligned}f_{M_{t}}(m)&=\int _{-\infty }^{m}f_{M_{t},W_{t}}(m,w)\,dw=\int _{-\infty }^{m}{\frac {2(2m-w)}{t{\sqrt {2\pi t}}}}e^{-{\frac {(2m-w)^{2}}{2t}}}\,dw\\[5pt]&={\sqrt {\frac {2}{\pi t}}}e^{-{\frac {m^{2}}{2t}}},\qquad m\geq 0.\end{aligned}}$

E o valor esperado

$\operatorname {E} [M_{t}]=\int _{0}^{\infty }mf_{M_{t}}(m)\,dm=\int _{0}^{\infty }m{\sqrt {\frac {2}{\pi t}}}e^{-{\frac {m^{2}}{2t}}}\,dm={\sqrt {\frac {2t}{\pi }}}$

Se em $t$ o processo de Wiener tem um valor conhecido $W_{t}$, é possível calcular a distribuição de probabilidade condicional do máximo no intervalo $[0,t]$ (vide a distribuição de probabilidade de pontos extremos de um processo estocástico de Wiener).

Autossemelhança

Uma demonstração do escalamento browniano, mostrando que$V_{t}=(1/{\sqrt {c}})W_{ct}$ para c decrescente. Note que as características gerais da função não mudam enquanto se aproxima e que a velocidade da ampliação na horizontal é igual ao quadrado da velocidade da ampliação na vertical.

Escalamento browniano

Para todo $c>0$, o processo $V_{t}=(1/{\sqrt {c}})W_{ct}$ é outro processo de Wiener.

Reversão de tempo

O processo $V_{t}=W_{1}-W_{1-t}$ para $0\leq t\leq 1$ é distribuído como $W_{t}$ para $0\leq t\leq 1$.

Inversão de tempo

O processo $V_{t}=tW_{1/t}$ é outro processo de Wiener.

Uma classe de martingales brownianos

Se uma função polinomial $p(x,t)$ satisfaz a equação diferencial parcial

$\left({\frac {\partial }{\partial t}}+{\frac {1}{2}}{\frac {\partial ^{2}}{\partial x^{2}}}\right)p(x,t)=0$

então o processo estocástico

$M_{t}=p(W_{t},t)$

é um martingale.

Exemplo: $W_{t}^{2}-t$ é um martingale, que mostra que a variação quadrática de $W$ em $[0,t]$ é igual a $t$. Segue-se que o tempo de primeira saída esperado de $W$ de $(-c,c)$ é igual a $c^{2}$.

Mais geralmente, para toda função polinomial $p(x,t)$, o seguinte processo estocástico é um martingale:

$M_{t}=p(W_{t},t)-\int _{0}^{t}a(W_{s},s)\,\mathrm {d} s,$

em que $a$ é a função polinomial

$a(x,t)=\left({\frac {\partial }{\partial t}}+{\frac {1}{2}}{\frac {\partial ^{2}}{\partial x^{2}}}\right)p(x,t).$

Exemplo: $p(x,t)=(x^{2}-t)^{2},$ $a(x,t)=4x^{2};$ o processo

$(W_{t}^{2}-t)^{2}-4\int _{0}^{t}W_{s}^{2}\,\mathrm {d} s$

é um martingale, que mostra que a variação quadrática do martingale $W_{t}^{2}-t$ on [0, t]$[0,t]$ é igual a

$4\int _{0}^{t}W_{s}^{2}\,\mathrm {d} s.$

Algumas propriedades de caminhos amostrais

O conjunto de todas as funções $w$ com estes propriedades é composto inteiramente por medidas de Wiener. Isto é, um caminho (função amostral) do processo de Wiener tem todas estas propriedades quase certamente.

Propriedades qualitativas

• Para todo $\varepsilon >0$, a função $w$ assume tanto valores (estritamente) positivos, como (estritamente) negativos em $(0,\varepsilon )$.
• A função $w$ é contínua em todo lugar, mas diferenciável em lugar nenhum (assim como a função de Weierstrass).
• Pontos do máximo local da função $w$ são um conjunto contável denso; os valores máximos são diferentes por pares; cada máximo local é agudo na seguinte acepção: se $w$ tem um máximo local em $t$, então

$\lim _{s\to t}{\frac {|w(s)-w(t)|}{|s-t|}}\to \infty .$

O mesmo se aplica a mínimos locais.

• A função $w$ não tem nenhum ponto de crescimento local, isto é, nenhum $t>0$ satisfaz as seguintes condições para algum $\varepsilon$ em $(0,t)$: em primeiro lugar, $w(s)\leq t$ para todo $s$ em $(t-\varepsilon ,t)$, e em segundo lugar, $w(s)\geq w(t)$ para todo $s$ em $(t,t+\varepsilon )$. O crescimento local é uma condição mais fraca do que aquela referente ao crescimento de $w$ em $(t-\varepsilon ,t+\varepsilon )$. O mesmo se aplica ao decrescimento local.
• A função $w$ é de variação limitada em todo intervalo.
• A variação quadrática de $w$ ao longo de $[0,t]$ é $t$.
• Os zeros da função $w$ são um conjunto perfeito denso em lugar nenhum com medida de Lebesgue 0 e dimensão de Hausdorff $1/2$ (portanto, incontável).

Propriedades quantitativas

Lei do logaritmo iterado

$\limsup _{t\to +\infty }{\frac {|w(t)|}{\sqrt {2t\log \log t}}}=1,\quad {\text{quase certamente}}.$

Módulo de continuidade

Módulo local de continuidade:

$\limsup _{\varepsilon \to 0+}{\frac {|w(\varepsilon )|}{\sqrt {2\varepsilon \log \log(1/\varepsilon )}}}=1,\qquad {\text{quase certamente}}.$

Módulo global de continuidade (Lévy):

$\limsup _{\varepsilon \to 0+}\sup _{0\leq s<t\leq 1,t-s\leq \varepsilon }{\frac {|w(s)-w(t)|}{\sqrt {2\varepsilon \log(1/\varepsilon )}}}=1,\qquad {\text{quase certamente}}.$

Tempo local

A imagem da medida de Lebesgue em $[0,t]$ sob o mapa $w$ (a medida imagem) tem uma densidade $L_{t}(\cdot )$. Assim,

$\int _{0}^{t}f(w(s))\,\mathrm {d} s=\int _{-\infty }^{+\infty }f(x)L_{t}(x)\,\mathrm {d} x$

para uma ampla classe de funções $f$ (nomeadamente, todas as funções contínuas, todas as funções localmente integráveis, todas as funções não negativas mensuráveis). A densidade $L_{t}$ é (mais exatamente, pode ser e será escolhida como) contínua. O número $L_{t}(x)$é chamado de tempo local em $x$ de $w$ ao longo de $[0,t]$. É estritamente positiva para todo $x$ do intervalo $(a,b)$, em que $a$ e $b$ são o menor e o maior valor de $w$ em $[0,t]$, respectivamente. Para $x$ fora deste intervalo, o tempo local evidentemente desaparece. Tratado como uma função de duas variáveis $x$ e $t$, o tempo local é ainda contínuo. Tratado como uma função de $t$ (em que $x$ está fixado), o tempo local é uma função singular correspondente à medida não atômica sobre o conjunto de zeros de $w$.

Estas propriedades de continuidade são razoavelmente não triviais. Considere que o tempo local também possa ser definido (como a densidade da medida imagem) para uma função suave. Por consequência, entretanto, a densidade é descontínua, a não ser que a função dada seja monótona. Em outras palavras, há um conflito entre o bom comportamento de uma função e o bom comportamento de seu tempo local. Neste sentido, a continuidade do tempo local para o processo de Wiener é outra manifestação da não suavidade da trajetória

Processos relacionados

Processos de Wiener com deriva (azul) e sem deriva (vermelho).

Processos de Wiener bidimensionais com deriva (azul) e sem deriva (vermelho).

Um gerador de movimento browniano é o produto do operador de Laplace-Beltrami por 0,5. A imagem acima é de um movimento browniano em uma variedade especial: a superfície de uma esfera.

O processo estocástico definido por

$X_{t}=\mu t+\sigma W_{t}$

é chamado de processo de Wiener com deriva $\mu$ e variância infinitesimal $\sigma ^{2}$. Estes processos representam todos os processos de Lévy contínuos.

Dois processos aleatórios no intervalo de tempo $[0,1]$ aparecem, grosso modo, quando se condiciona o processo de Wiener a desaparecer nos dois extremos de $[0,1]$. Quando não se condiciona mais, o processo assume tanto valores positivos, como negativos em $[0,1]$ e é chamado de ponte browniana. Condicionado a permanecer positivo em $[0,1]$, o processo é chamado de excursão browniana. Em ambos os casos, um tratamento rigoroso envolve um procedimento limitante, já que a fórmula $P(A|B)=P(A\bigcap B)/P(B)$ não se aplica quando $P(B)=0$.

Um movimento browniano geométrico pode ser escrito como

$e^{\mu t-{\frac {\sigma ^{2}t}{2}}+\sigma W_{t}}.$

É um processo estocástico usado para modelar processos que nunca podem assumir valores negativos, tais como os valores de ações.

O processo estocástico

$X_{t}=e^{-t}W_{e^{2t}}$

é distribuído como o processo de Ornstein-Uhlenbeck.

O tempo de chegada a um único ponto $x>0$ pelo processo de Wiener é uma variável aleatória com distribuição de Lévy. A família destas variáveis aleatórias (indexadas por todos os números positivos $x$) é uma modificação contínua à esquerda do processo de Lévy. A modificação contínua à direita deste processo é dada pelos tempos de primeira saída a partir de intervalos fechados $[0,x]$.

O tempo local $L=(L_{t}^{x})_{x\in R,t\geq 0}$ de um movimento browniano descreve o tempo que o processo passa no ponto $x$. Formalmente,

$L^{x}(t)=\int _{0}^{t}\delta (x-B_{t})\,ds$

em que $\delta$ é a função delta de Dirac. O comportamento do tempo local é caracterizado pelos teoremas de Ray-Knight.

Martingales brownianos

Considere $A$ um evento relacionado ao processo de Wiener (mais formalmente, um conjunto, mensurável no que se refere à medida de Wiener, no espaço de funções), e $X_{t}$ a probabilidade condicional de $A$ dado o processo de Wiener no intervalo de tempo $[0,t]$ (mais formalmente, a medida de Wiener do conjunto de trajetórias cuja concatenação com a trajetória parcial dada em $[0,t]$ pertence a $A$). Então, o processo $X_{t}$ é um martingale contínuo. Sua propriedade martingale deriva imediatamente das definições, mas sua continuidade é um fato muito especial – um caso especial de um teorema geral que afirma que todos os martingales brownianos são contínuos. Um martingale browniano é, por definição, um martingale adaptado à filtração browniana, sendo esta, por definição, a filtração gerada pelo processo de Wiener.

Movimento browniano integrado

A integral do tempo do processo de Wiener

$W^{(-1)}(t):=\int _{0}^{t}W(s)ds$

é chamada de movimento browniano integrado ou processo de Wiener integrado. Aparece em muitas aplicações e pode-se mostrar por cálculo que tem distribuição $N(0,t^{3}/3)$, usando o fato de que a covariância do processo de Wiener é $t\wedge s=\min(t,s)$.

Mudança de tempo

Todo martingale contínuo (a partir da origem) é um processo de Wiener com tempo mudado.

Exemplo: $2W_{t}=V(4t)$, em que $V$ é outro processo de Wiener (diferente de $W$, mas distribuído como $W$).

Exemplo: $W_{t}^{2}-t=V_{A(t)}$, em que $A(t)=4\int _{0}^{t}W_{s}^{2}\,\mathrm {d} s$ e $V$ é outro processo de Wiener.

Geralmente, se $M$ for um martingale contínuo, então $M_{t}-M_{0}=V_{A(t)}$ , em que $A(t)$ é a variação quadrática de $M$ em $[0,t]$ e $V$ é um processo de Wiener.

Corolário: Considere $M_{t}$ um martingale contínuo e

$M_{\infty }^{-}=\liminf _{t\to \infty }M_{t},$

$M_{\infty }^{+}=\limsup _{t\to \infty }M_{t}.$

Então, apenas os dois casos seguintes são possíveis:

$-\infty <M_{\infty }^{-}=M_{\infty }^{+}<+\infty ,$

$-\infty =M_{\infty }^{-}<M_{\infty }^{+}=+\infty ;$

outros casos (tais como $M_{\infty }^{-}=M_{\infty }^{+}=+\infty ,$   $M_{\infty }^{-}<M_{\infty }^{+}<+\infty$, etc.) são de probabilidade $0$.

Especialmente, um martingale contínuo não negativo tem um limite finito (como $t\rightarrow \infty$) quase certamente.

Tudo o que foi afirmado nesta subseção sobre martingales também se aplica a martingales locais.

Mudança de medida

Uma classe ampla de semimartingales contínuos (especialmente, de processos de difusão) está relacionada ao processo de Wiener por meio de uma combinação de mudança de tempo e mudança de medida.

Usando este fato, as propriedades qualitativas afirmadas acima para o processo de Wiener podem ser generalizadas para uma classe ampla de semimartingales contínuos.

Processo de Wiener de valores complexos

O processo de Wiener de valores complexos pode ser definido como um processo aleatório de valores complexos da forma $Z_{t}=X_{t}+iY_{t}$ em que $X_{t},Y_{t}$ são processos de Wiener independentes (de valores reais).

Autossemelhança

O escalamento browniano, a reversão de tempo e a inversão de tempo são iguais aos do caso com valores reais.

Quanto à invariância de rotação, para cada número complexo $c$ tal que $\left\vert c\right\vert =1$, o processo $cZ_{t}$ é outro processo de Wiener de valores complexos

Mudança de tempo

Se $f$ for uma função inteira, então, o processo $f(Z_{t})-f(0)$ é um processo de Wiener de valores complexos com mudança de tempo.

Exemplo: $Z_{t}^{2}=(X_{t}^{2}-Y_{t}^{2})+2X_{t}Y_{t}i=U_{A(t)}$ em que

$A(t)=4\int _{0}^{t}|Z_{s}|^{2}\,\mathrm {d} s$

e $U$ é outro processo de Wiener de valores complexos.

Em contraste com o caso de valores reais, um martingale de valores complexos geralmente não é um processo de Wiener de valores complexos com mudança de tempo. Por exemplo, o martingale 2X_t + iY_t$2X_{t}+iY_{t}$ não é (aqui $X_{t},Y_{t}$ são processos de Wiener independentes, assim como antes).

Ver também

Generalidades

• Espaço de Wiener abstrato
• Espaço de Wiener clássico
• Fractal

Amostragem de caminhos

• Método de Euler-Maruyama

Ligações externas

• Movimento browniano para crianças em idade escolar (em inglês)
• Movimento browniano: 'diverso e ondulante' (em inglês)
• O que Brown viu e você também pode ver (em inglês)
• A previsão de Einstein finalmente observada um século depois (em inglês)