Proporção áurea

Proporção áurea, número de ouro, número áureo, secção áurea, proporção de ouro é uma constante real algébrica irracional denotada pela letra grega (PHI), em homenagem ao escultor Phideas (Fídias), que a teria utilizado para conceber o Parthenon, e com o valor arredondado a três casas decimais de 1,618. Também é chamada de se(c)ção áurea (do latim sectio aurea),[1] razão áurea,[2] razão de ouro, média e extrema razão (Euclides), divina proporção, divina seção (do latim sectio divina), proporção em extrema razão,[3] divisão de extrema razão ou áurea excelência.[4][5] O número de ouro é ainda frequentemente chamado razão de Phidias.[6][7][8]
Desde a Antiguidade, a proporção áurea é usada na arte.[9] É frequente a sua utilização em pinturas renascentistas, como as do mestre Giotto. Este número está envolvido com a natureza do crescimento. Phi (não confundir com o número Pi ), como é chamado o número de ouro, pode ser encontrado de forma aproximada no homem (o tamanho das falanges, ossos dos dedos, por exemplo), nas colmeias, entre inúmeros outros exemplos que envolvem a ordem de crescimento na natureza.
Justamente por ser encontrado em estudos de crescimento, o número de ouro ganhou um status de "ideal", sendo alvo de pesquisadores, artistas e escritores. O fato de ser apoiado pela matemática é que o torna fascinante.

Propriedades matemáticas[editar | editar código-fonte]
Definição algébrica[editar | editar código-fonte]
Dois valores positivos estão em razão áurea se sua razão é igual à razão da sua soma pela maior das quantidades. Algebricamente, dados e , , então:
Onde representa a razão áurea. O seu valor é constante e pode ser encontrado a partir da definição anterior.
Usando a parte direita da equação, vemos que o que pode ser substituído na parte esquerda, resultando em:
Cancelando b em ambos os lados, temos:
Multiplicando ambos os lados por resulta:
Finalmente, subtraindo de ambos os membros da equação e multiplicando todas as parcelas por encontramos:
- que é uma equação quadrática da forma em que
Agora, basta resolver essa equação quadrática. Pela fórmula resolutiva de uma equação quadrática:
A única solução positiva dessa equação quadrática é a seguinte:
- que é o número
Sequência de Fibonacci[editar | editar código-fonte]

O número áureo está presente na fórmula do termo geral da Série de Fibonacci:
O número áureo pode ser aproximado pela divisão do n-ésimo termo da Série de Fibonacci pelo termo anterior, sendo a aproximação tanto melhor quanto maior for n. Por exemplo:
Série de frações[editar | editar código-fonte]
O número áureo também pode ser encontrado através de frações contínuas, normalmente representadas como [a,b,c,d,e,...], o que resulta em:[10]
A aproximação do número áureo vem com a quantidade de números 1 em uma representação de Série de Frações. O valor varia em torno do número áureo, sendo maior ou menor alternadamente, mas sempre se aproximando deste.
Um número irracional sempre pode ser aproximado por números racionais, e os convergentes da representação em fração contínua são as melhores aproximações. A aproximação é tão melhor quando se corta a expansão em um coeficiente grande; por exemplo, uma boa aproximação de π = [3; 7, 15, 1, 292, 1, 1, 1, ...] é obtida ao se tomar π ~= [3; 7, 15, 1] = 3.141592654... Como todos os coeficientes da fração contínua de φ são um, todas suas aproximações por racionais são ruins - de fato, φ é o pior número para ser aproximado por racionais.[10]
Série de raízes[editar | editar código-fonte]
Proporção áurea na natureza[editar | editar código-fonte]
Figuras geométricas[editar | editar código-fonte]
Um decágono regular, inscrito numa circunferência, tem os lados em proporção áurea com o raio da circunferência.
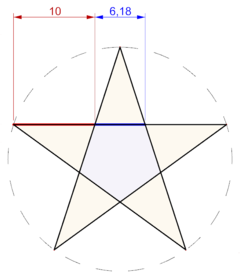
Um pentagrama regular é obtido traçando-se as diagonais de um pentágono regular. O pentágono menor, formado pelas interseções das diagonais, também está em proporção com o pentágono maior, de onde se originou o pentagrama. A razão entre as medidas dos lados dos dois pentágonos é igual ao quadrado da razão áurea. A razão entre as medidas das áreas dos dois pentágonos é igual a quarta potência da razão áurea.
Chamando os vértices de um pentagrama de A, B, C, D e E, o triângulo isósceles formado por A, C e D tem seus lados em relação dourada com a base, e o triângulo isósceles A, B e C tem sua base em relação dourada com os lados.
Quando Pitágoras descobriu que as proporções no pentagrama eram a proporção áurea, tornou esse símbolo estrelado como a representação da Irmandade Pitagórica. Esse era um dos motivos que levava Pitágoras a dizer que "tudo é número", ou seja, que a natureza segue padrões matemáticos.
Vegetais[editar | editar código-fonte]
Como os vegetais não têm formas exatas, a ponto de serem construídos com régua e compasso, a divina proporção, bem como a série Fibonacci, só podem ser encontradas por aproximação. Portanto, seria inexato atribuir correlações perfeitas entre a natureza e uma formulação idealizada pelo homem.[11][12]
Animais[editar | editar código-fonte]
Nos animais, as medidas também são aproximadas e os desenhos e as modelagens, produzidos dentro desse cânone ideal, são criações exclusivas de artistas, "designers", ilustradores, escultores, entre outros.[11][12]
Corpo humano[editar | editar código-fonte]

- A altura do corpo humano e a medida do umbigo até o chão.
- A altura do crânio e a medida da mandíbula até o alto da cabeça.
- A medida da cintura até a cabeça e o tamanho do tórax.
- A medida do ombro à ponta do dedo e a medida do cotovelo à ponta do dedo.
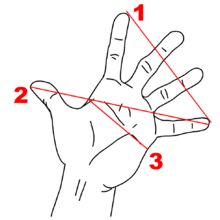
- O tamanho dos dedos e a medida da dobra central até a ponta.
- A medida da dobra central até a ponta dividido e da segunda dobra até a ponta.
- A medida do seu quadril ao chão e a medida do seu joelho até o chão.
Essas proporções anatómicas ideais foram representadas pelo "Homem Vitruviano", obra de Leonardo Da Vinci.
- Dimensão do útero em mulheres jovens (16 e 20 anos), segundo o pesquisador Jasper Vergtus, da Universidade de Leuven.[13]
Aplicações[editar | editar código-fonte]
O homem, em muitas ocasiões, tem buscado o ideal da perfeição nas linguagens artísticas.
Arte[editar | editar código-fonte]

A proporção áurea foi muito usada na arte, em obras como O Nascimento de Vênus, quadro de Botticelli, em que Afrodite está na proporção áurea. Essa proporção estaria ali aplicada pelo motivo de o autor representar a perfeição da beleza.
Em O Sacramento da Última Ceia, de Salvador Dalí, as dimensões do quadro (aproximadamente 270 cm × 167 cm) estão numa razão áurea entre si. Na história da arte renascentista, a perfeição da beleza em quadros foi bastante explorada com base nessa constante. Vários pintores e escultores lançaram mão das possibilidades que a proporção lhes dava para retratar a realidade com mais perfeição.
A Mona Lisa, de Leonardo da Vinci, tem a proporção áurea nas relações entre o tronco e a cabeça, bem como nos elementos da face, mas isso é uma característica inerente ao ser humano e tais proporções podem ser encontradas na maioria das pinturas em que a anatomia tenha sido respeitada.[15] Medições feitas por computador mostraram que os olhos de Mona Lisa estão situados em subdivisões áureas da tela.[14]
Retângulo dourado[editar | editar código-fonte]

Em geometria, o retângulo de ouro surge do processo de divisão em média e extrema razão, de Euclides. Ele é assim chamado porque ao dividir-se a base desse retângulo pela sua altura, obtêm-se o número de ouro 1,618.[16]
Música[editar | editar código-fonte]
O número de ouro está presente em diversas obras de compositores clássicos, sendo o exemplo mais notável a famosa Sinfonia n.º 5, de Ludwig van Beethoven.[17] O compositor húngaro Béla Bartók também utilizou esta relação de proporcionalidade constantemente em sua obra,[18] assim como o fez o francês Claude Debussy em diversas composições.[19]
No jazz, há músicos que usam os números da série Fibonacci na divisão rítmica e dos compassos.[20]
Literatura[editar | editar código-fonte]
No livro "O Número de Ouro", Matila Ghyka demonstrou a existência da proporção áurea em textos escritos por Victor Hugo, Shakespeare, Paul Valéry, Pierre Louys, entre outros. Na pesquisa, Ghyka relacionou as estrofes de acordo com o ritmo da leitura, o que ele chamou de ritmo prosódico.[21]
Cinema[editar | editar código-fonte]
O diretor russo Sergei Eisenstein utilizou o número no filme O Encouraçado Potemkin para marcar os inícios de cenas importantes da trama, medindo a razão pelo tamanho das fitas de película.
Arquitetura[editar | editar código-fonte]
Na Pirâmide de Quéops, no Egito, cada bloco é 1,618 vezes maior que o bloco do nível logo acima e também, as câmaras em seu interior seguem esta proporção, de forma que os comprimentos das salas são 1,618 vezes maiores que as larguras. Ainda, nas ruínas do Parthenom, na Grécia, são notadas inúmeras presenças da razão áurea.[22]
Mercado Financeiro[editar | editar código-fonte]
A aplicação da seqüência e da razão de ouro, mais especificamente o seu inverso, 0,618, na análise dos padrões de reversão de ações é o ponto que liga Fibonacci ao mercado de ações. São pontos baseados nos números descobertos pelo italiano que, segundo muitos analistas, podem indicar os níveis de suporte ou resistência de um papel.[23]
Nos dias atuais[editar | editar código-fonte]
A proporção áurea é utilizada como referência para o desenvolvimento de logótipos, materiais gráficos e obras audiovisuais,[24] por muitos "designers" e diretores de arte.
Proporção áurea e regra dos terços[editar | editar código-fonte]
É muito comum, dentro da área audiovisual e fotografia, utilizar-se a regra dos terços, porém muito se defende a substituição dessa técnica pela Proporção Áurea,[25] já que por sua vez a regra do ponto de ouro é intrínseca à natureza e superior à regra dos terços primária, como descrito pelo fotógrafo britânico Jon Sparkman[26]
Linha do tempo[editar | editar código-fonte]
Linha do tempo baseada nos estudos de Priya Hemenway:[27]
- Phidias (490–430 a.C.) projetou o Partenon que contém proporções áureas.
- Platão (427–347 a.C.), no seu Timeu, descreveu os sólidos platônicos: tetraedro, hexaedro (cubo), octaedro, dodecaedro e icosaedro. Podem ser encontradas proporções áureas em partes dos sólidos.[28]
- Euclides (325–265 a.C.), em sua obra Os Elementos, registrou a construção geométrica divisão em média e extrema razão (em grego: ἄκρος καὶ μέσος λόγος).[29]
- Fibonacci (1170–1250) mencionou a sequência numêrica conhecida como Sequência de Fibonacci; que são aproximações do número de ouro.
- Luca Pacioli (1445–1517) estudou a "divina proporção" em sua obra de mesmo nome. O termo foi sugerido por Leonardo Da Vinci.
- Michael Maestlin (1550–1631) publicou a fração decimal do número de ouro.
- Johannes Kepler (1571–1630) provou que a proporção áurea é o limite da relação entre os números consecutivos da série Fibonacci[30] e descreveu a proporção áurea como uma "joia preciosa": "A geometria tem dois grandes tesouros: um é o Teorema de Pitágoras, e o outro é a divisão áurea".
- Charles Bonnet (1720–1793) apontou a presença da série Fibonacci nas espirais logarítmicas presentes nas plantas, tanto no sentido horário, como no anti-horário.
- Martin Ohm (1792–1872) acredita-se ter sido o primeiro a usar o termo "segmento áureo" para descrever essa relação, em 1835.[31]
- Édouard Lucas (1842–1891) deu à sequência numérica o nome de Série de Fibonacci.
- Mark Barr (século XX) sugeriu a letra grega phi ( 'φ' ), que era a letra inicial do nome do escultor grego Fídias, para simbolizar a proporção áurea.[32]
Referências
- ↑ Summerson John, Heavenly Mansions: And Other Essays on Architecture (New York: W.W. Norton, 1963) p. 37. "E o mesmo se aplica em arquitetura, aos retângulos que representam estas e outras proporções (e.g. a 'seção áurea')."
- ↑ Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. ISBN 0-7679-0815-5
- ↑ Euclid, Elements, Book 6, Definition 3.
- ↑ Piotr Sadowski, The Knight on His Quest: Symbolic Patterns of Transition in Sir Gawain and the Green Knight, Cranbury NJ: Associated University Presses, 1996
- ↑ Richard A Dunlap, The Golden Ratio and Fibonacci Numbers, World Scientific Publishing, 1997
- ↑ Jay Hambidge, Dynamic Symmetry: The Greek Vase, New Haven CT: Yale University Press, 1920
- ↑ William Lidwell, Kritina Holden, Jill Butler, Universal Principles of Design: A Cross-Disciplinary Reference, Gloucester MA: Rockport Publishers, 2003
- ↑ Pacioli, Luca. De divina proportione, Luca Paganinem de Paganinus de Brescia (Antonio Capella) 1509, Venice.
- ↑ György Dóczi (1981). O Poder dos limites: harmonias e proporções na natureza, arte & arquitetura. [S.l.]: Shambhala. Capítulo IV
- ↑ a b Kiritchenko, Valentina, Continued Fractions, p.12 [1]Arquivado em 16 de outubro de 2014, no Wayback Machine. [em linha]
- ↑ a b György Dóczi (1981). «O Poder dos limites». Amazon.com. Consultado em 7 de julho de 2014
- ↑ a b Robert Lamb. «How are Fibonacci numbers expressed in nature?». Howstuffworks.com. Consultado em 7 de julho de 2014
- ↑ ABC.es. Él número áureo, descubierto en el útero. Acesso 16 de agosto de 2012.
- ↑ a b Denis Mandarino (27 de agosto de 2011). «A divisão áurea por detrás do olhar de Mona Lisa». Portal Alô Artista. Arquivado do original em 24 de julho de 2015
- ↑ Ostrower, Fayga (1983). Universos da Arte. [S.l.]: Campus
- ↑ Putnoki, José Carlos - Elementos de Geometria e desenho geométrico. Vol. 1. Ed. Scipione, São Paulo, 1989. p. 140.
- ↑ Haylock, Derek. Mathematics Teaching, Volume 84, p. 56-57. 1978
- ↑ Ernö Lendvai - Béla Bartók: An Analysis of his Music
- ↑ Roy Howat - Debussy in Proportion
- ↑ Steve Coleman. «The Dozens». Jazz.com. Consultado em 14 de janeiro de 2014. Arquivado do original em 9 de fevereiro de 2014
- ↑ Matila Ghyka (1984). El número de oro. [S.l.]: Poseidon
- ↑ Tanure, Antônio Carlos. «Proporção Áurea e Sequência de Fibonacci». Consultado em 28 de agosto de 2019
- ↑ «Números de Fibonacci: forma simples para tentar prever reversões de mercado». Consultado em 28 de agosto de 2019
- ↑ Nerival Ferraz (3 de novembro de 2016). «Finalmente! Aprenda a aplicar Proporção Áurea». http://designculture.com.br. Consultado em 3 de novembro de 2016
- ↑ Ruca Souza (25 de janeiro de 2017). «Por que a Proporção Áurea é a melhor do que a Regra dos Terços». http://iphotochannel.com.br. Consultado em 25 de janeiro de 2017
- ↑ Jon Sparkman (3 de outubro de 2016). «Por que a relação de ouro é melhor do que a regra de terceiros». http://sparkman.co.uk. Consultado em 3 de outubro de 2016
- ↑ Hemenway, Priya (2005). Divine Proportion: Phi In Art, Nature, and Science. Nova Iorque: Sterling. pp. 20–21. ISBN 1-4027-3522-7
- ↑ Platão (360 AC). «Timaeus» (em inglês). Traduzido por Benjamin Jowett. The Internet Classics Archive. Consultado em 30 de maio de 2006
- ↑ «O número de ouro». Universidade Federal Fluminense. Consultado em 23 de junho de 2016. Arquivado do original em 4 de agosto de 2016
- ↑ James Joseph Tattersall (2005). Elementary number theory in nine chapters 2ª ed. [S.l.]: Cambridge University Press. p. 28. ISBN 978-0-521-85014-8
- ↑ Underwood Dudley (1999). Die Macht der Zahl: Was die Numerologie uns weismachen will. [S.l.]: Springer. p. 245. ISBN 3-7643-5978-1
- ↑ Cook, Theodore Andrea (1979) [1914]. The Curves of Life. Nova Iorque: Dover Publications. ISBN 0-486-23701-X
Bibliografia[editar | editar código-fonte]
- Cole, K. C.. O Universo e a Xícara de Chá. São Paulo: Record, 2006. 294p.
- Doczi, György. O Poder dos limites. São Paulo: Mercuryo, 1990.
- Livio, Mario. Razão áurea: a história do phi. São Paulo: Record, 2006. 336p.























![{\displaystyle F(n)={\frac {\phi _{+}^{n}-\phi _{-}^{n}}{\phi _{+}-\phi _{-}}}={\frac {1}{\sqrt {5}}}\left[\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3800d742e7a9b1d96a05bbd71eb197028208b3be)







![{\displaystyle [1;1]=1+{\frac {1}{1}}=1+1=2.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1603cd46394c3872b7e0faa2d42ac7f063db908)
![{\displaystyle [1;1,1]=1+{\frac {1}{1+{\frac {1}{1}}}}=1+{\frac {1}{2}}={\frac {3}{2}}=1,5.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8128db6f6e63ac77f74efe3cb9c8ddb63d69cdbc)
![{\displaystyle [1;1,1,1]=1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1}}}}}}=1+{\frac {1}{\frac {3}{2}}}=1+{\frac {2}{3}}={\frac {5}{3}}=1,666.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb11565df8cff4d6d08c0409cb27d32a605d8317)
![{\displaystyle [1;1,1,1,1]=1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1+{\frac {1}{1}}}}}}}}=1+{\frac {1}{\frac {5}{3}}}=1+{\frac {3}{5}}={\frac {8}{5}}=1,6.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a08d6ac6ac425f4dc7ef411b2781c2e0dc7d757)

